WHAT THE FUCK THO.




        WHERE DID LOVE GO?



                             FIVE

                      FOUR

              THREE

   TWO



 BREAKIN BROKE BRO




AIMIN AT YA HULL


    LIKE A BUFFALO


FUCKS A SIEGE DOE?


                

 


                                              (OOOOHHHHHHH)




NO BREAD BRO       NO BRIO’            


ALL THE DETAILS
      IN THE DEVOLS




                     GENS KEEP TRACK O’

                           

           NOTHIN’ DOWN LOW ↓


           BUT I GOT A PARK



UP IN OL’ OLL’ ↑


                  (YEEEEEEEEEEEE)




     GIT A HAMMAH,

AND THE SICKOLE ☭               IS A HANDSPIKE
   FOR THE SKYHOLE



       MISS AMERICA



            RED TIGHT BLOWHOLE


            UNSPIKE THE CANNON
      IN THE GUNHOLE

         


TIME A WASTIN

    ON THE GUNROLL

TICK TOCK SHELL SHOCK
    HEAR THE GUN BLOW


STEAL A 40KILO AND POUND HER BIRTHHOLE



                     (AWWWWWWWWWWWWW)





CUCK A NEAPOL,
    DESTRESS HIS DAMSOL

SHE GIVES YOU HEAD     WHILE HIS HEAD ROLL

STOLEN ON THE CLOCK,
    40-KILO

NEO-/POL/ WIFE:
    BROWN AND TWELVE YEARS OLD




             (WOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO)




      WHAT THE FUCK THO



WHERE DID LOVE GO?



        (OH)



                          FIVE


             FOUR




           THREE




     TWO

 


                    (SHIIIIIIIIIIIIIIIIIIIIIII)


              COMMANDER GHOST          HE’S A NO SHOW


              HE HINTER     I’M FRONT ROW



         CANT READ A ROOM         CANT READ A MAP YO.



             WEARS A MUSTACHE PAINTS LIKE AN ART HOE







IM ON THE RAMPART MAPPING OUTPOSTS


I LISTEN TO DESCARTER YOU LISTEN TO CARTEAUX♩


FIND A FUCCBOW


        SHOOT YOUR ARROW


                    WHITE HOT SHOT





SO HOMO



                               (AIYAYAIIYAYAYAYIIAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAaaaA)




AINT NO CART THO. THEY ALL WAGONS


           × GONNA FIB BRO. ITS ALL FIBROE.


THEY ALL NAVAL. ALL CANNONS.



       ALL FROM THE WALL TO THE WIND⊗W






WHAT THE FUCKKKKKKKK THO. WHERE THE LOVE GO.



  FIVE


    FOUR



        THREE




          TWELVE WAIT WHAT YO—




               (OOOOOOOOOOOOOOOOOOOHHHHHHHHHHHHHHHHHH)





        GOTTA UPROAR.






GOTTA UPTHROW ✊🏾



            GOTTA LIVE_DOWN.




            GOTTA ^UPGROW.






    ITS ALL NO.



           ITS ALL KNOWN.










There’s nothing here....





but outgrowth.











    WHAT THE FUCK YO.




         WHERE DID LOVE GO.



          CANT BUY IT BABE.








NO BREAD,
    NO DOUGH








THE STORES CLOSE


               THE SCHEMES CLOSED



ARREARS CLOSE LOW


                                         (AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA)


AND YOU SELL LOW




what’s that? Closed subschemes? Ooh, is that foundational? Passed over while scurrying about the field? Lol. Which ones the devil? You got an eye for that? An eye for the devil? I’ll need a damn good chief of staff, man. You know: Someone to run shit, on behalf of someone else. That’s what I’m missing: A master of administration. I need a head-and-chain to carry around with me. I’ll need a bit more brain space. I need a human being to park mental information into. Who wants to be the ”mental reserve” for someone else? How degrading, they say. But this is how magic is made. Cooperation, and devotion. You know what I need? A pastor with a big, fat Qari memory at one’s side. the A Berthierian wonder. An Admax of an Admin. An admin cum general-on-call. Someone jussssst a tad shorter than me–an inch or two. A dirt-eater, who snuffs out maps with debris. Someone that is coordinated with me, you see. We need to be able to dance, and he needs to know the steps. And he needs to keep the steps confidential. He needs to finish my sentences like a wife. He needs to be connected to my brain in invisible threads. His motor functions should respond to my movements and vice-versa–we need to move in messy synchronization. Get you a good wife: Can you? One who’ll present your amendment with the force of their good image. One that’ll pretie your ties and have breakfast ready by the time you’re down to dine. One that’ll keep refilling your coffee like an IHOP waitress. One that’ll watch you bite deep into a barbeque sauce smothered steak, your mouth-half-open chewing, and be at the ready with a napkin to wipe your lips. One that’ll entertain your guests, make em feel like home. One that’ll make em feel like she’s their wife, or two. She can remember names and faces even better than you. Make em feel good. Butter em up. Feed you thickly buttered waffles while you’re looking down at a map, or two. Be the liason tween you and your men–be your guard, the intermediary at the front desk. The preview; the pre-you. A woman can’t do any of that. Not two, not three. You’ll need a young man. Because he’ll need to be your notes; read books on your behalf–read: not just ”read books”, but read them as if you, the infamous non-reader, were reading them. He’ll need to vice you, and thus be malebrained. Have man-to-men with your underlings, and be able smooth-talk a vicomtesse. Act like a boyish son to a septuagenarian superior and a firebrand to a septuagenarian enemy. He’ll need to be able to run the show when you’re off in the East, without stealing it. Yes: All his intrigue should be directed away from you, outward from you, spun out from your person like the webs of a moth. Can you find someone that can be you, in all but optics. Can someone be your copy, but not in your image? Is that a thing? Cause that’s what I need. Someone who is me in everything except where it counts: On the ballot. I need that sort of loyalty. The one who’ll kiss my dick under a desk.

4.4: Prelude

The original intention of this post was to solve this:



In trying to do so, I got thrown into a journey of administrative overhead that is now ballooning into something else entirely. This turn of events has been so bizarre, in fact, we may even make it to section 5. So let’s begin with section 2:

2.3

 

EQHIORWQORHIWQORIJWQOIRHQWIHRWQ0IHRQ0WHJR0WQHRJ0WQHJR0WQHJR0WQHJRWQHJRWQIHROQWIHROIWQHROIWQHROIQHRWOIQWHROIWQHOIHQRWOIHJWQORIHJWQOIRHQORHWQOIHROIQHJROIWQHROIWQHROIWQHROWQIHROIQWHROIWQJOIRHJOIWQHOIWQHOIRWQHJOIWQHTOIQHTOIWQHOIHQOIHJRWQOIWHJQOIHJWQROIHWQOIHJWRQOIQHJORIWQJHOIWQHJROIWQHROIWQHROIWQRJOWJEQOJEWQOIJEWQOIJEWQOIJEWQJOIEWQJOIEWQJOIEWQEOIJWQOIJEWQOIJEWQOJIEWQOJIWQEOJIEWQOJIEWQJOWQEJOIWQJOWQJOIWQJEOWQIJEOQIWJEOWIQJEOIWQJEOWIQJEOIWQJEOWQJEOIWQJEOIWQJEOWQIJEOWIQJEOQWJEOIWQJEOWQJEOIWQJEOQWJEOIWQJEOIQHROIJREOIWQHJREOIWQHJROIJROIWQHJREOIWQHJROIWQHJROIHJRWOIHWQOIHJRWQOIHJRWQOIHRWQOIHJRWQOIHWQHOIWQOIHJWQIHJORWOHIWQOIHWQOIHWQOIHRWOIHRWQHOIRWQOIHJRWQOIHRWQOIHRWQOIHJRWQOIHJRWQOIHJRWQOWIRQOIHJWQROIHEWQJOIWQOIJWQHOHQWROIHRWQRHOIWQHQWRWQPRIQWOURWQUROWUQROWQUJORWQUJORWQJUORWQIORQWRWQJROWRIWOQQIOWQUEOWWQUWUUWQRQUIJROWQUEOWQQIUEWOURWQOUEOWQUROWQURWQWQUWQIUROUEWWUWQROIEWOQURIOWQUROWQIREOWQURIOQUROWQWQUROWQIUROWQUEOWQRIUOWQIUREOWQRUOWQEUJOWQRWQQJU

A

 

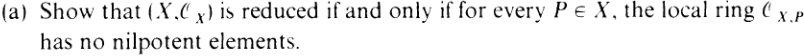
By the way, why restrict the term ”reduced” to schemes? Why not also talk about ”reduced sheaves” and ”reduced rings” with the obvious definitions. With that terminology, this part asks us to prove

So let’s start with...

0.0.1 only if

Let X be reduced, and let P ∈ X. Let U = SpecA be an open affine neighborhood of P in X. Then 𝒪_X(U) = A is reduced. We want to show that 𝒪_X,P = A_P is reduced. Now suppose we had a nilpotent element in A_P. i.e. suppose we had

	∈ AP
with( )n	= 0

 


for some n > 0. Then, by the definition of localization, there is some s′ P such that

s′(xn − sn ⋅ 0)	= 0
s′⋅ xn	= 0
(s′)n ⋅ xn	= 0
(s′⋅ x)n	= 0
s′⋅ x	= 0

 


That last equality follows from the fact that A is reduced.  


UH OH! WE’RE STUCK, HOLY-HEART!!! A_P AINT NECESSARILY NO INTEGRAL DOMAIN. I CANT USE THE ZERO PRODUCT PROPERTY. WHAT DO? WHAT DO? PANIC PANIC PANIC. Calm down: We’re still in A_P, not A, remember? s′ P, remember?If s′x = 0, then..

(1∕s′) ⋅ s′x	= 0
x	= 0
x∕s	= 0

 


And there she is

0.0.2 if

Now we suppose that 𝒪_X,P is reduced for all P. I’ll perform is a sheaf-theoretic argument–no affines necessary: Suppose U is open in X, and let x ∈𝒪_X(U) such that xⁿ = 0. Note that to say that each stalk is reduced, gives us that for each P ∈ U, there is a neighborhood V of P such that 𝒪_X(V ) is reduced. Consider the restriction map ρ from U to V . Then

xn	= 0
ρ(xn)	= 0
(ρ(x))n	= 0
ρ(x)	= 0

 


The last equality following from reducedness. But since x is locally 0, it’s 0 everywhere. Done.

B

 

This is extremely trivial, because it is simply the map

𝒩 = , by the way, is what we know as the nilradical.

C

 

So we need  

Where X is reduced. Which, dropping down to affines and flipping over to algebra, corresponds to

 



where A is reduced. Of course, this forces the definition of g as

g : Bred → A
[b] f(b)

 


So if g exists, it is unique. To show that it does exist, we have to check that the forced definition is well-defined. If [b] = [b′] in B_red = B∕ , then

b − b′	∈
∃n > 0 : (b − b′)n	= 0
f(b − b′)n	= 0
f(b − b′)	= 0	(since A is reduced)
f(b)	= f(b′)
g([b])	= g([b′])

 


Done.

3.11

 



Closed subschemes are a bit more iffy that open ones.



There is crucial fact we handled in an earlier exercise, which Hartshorne doesn’t bring up here. That, for affine schemes, closed immersions correspond to surjective ring morphisms. So, as you’d expect, reducing to affines and getting surjectivity in algebraworld will be our primary method for showing that something is a closed immersion. And thus, a lemma:

Lemma: Closed immersions is a local property

Given f : Y → X a closed immersion, suppose Y = ⋃ _iV _i is an open cover of Y , and X = ⋃ U_i is an open cover of X with V _i ⊂ U_i. Then if each restriction of f_i : V _i → U_i is a closed immersion, then f is a closed immersion

Proof

The surjectivity property on the ”sheaf side” of things is trivial, because in that case we’ve already shown that surjectivity is local. So we are done as long as we show that a continuous map of spaces f : X → Y is closed if it is locally closed.

Let’s begin: If f is locally closed on the open cover X = ⋃ _iU_i, let C ⊂ X be a closed set. Then

f(C)	= f(C ∩ X)
	= f(C ∩⋃ iUi)
	= f(⋃ iC ∩ Ui)
	= ⋃ if(C ∩ Ui)

 


And here’s where the story ends. Someone shoot me.Those 4 lines you see above is all I had for 4 entire days. 4 entire days were spent musing over those 4 lines. Count the beats: Bru-tal-ly-stumped. Stuck in a 4/4, all the way up to 5/5, upon which I ”assumed” it and tried moving on–but couldnt properly handle 4.4: I ran into more ”glueing” problems along the way, and if I can assume closed maps glue, well, why can’t I assume everything glues? That’s a dangerous assumption. After all, separated morphisms don’t glue, for instance. That’s a fairly big counterexample for the section named ”Separated and Proper Morphisms.” So in trying to ”move on,” the ass-sucking ghost of this lemma kept coming back to haunt me, and I kept getting drawn back to it, and getting restuck on it, and this continued for a week while ive been caught in other tasks. From 5/5 to 5/10, I was stuck in an odd waltz, drawn repeatedly back to this atrocity. My first obstacle in getting to 4.4 was... this. Not algebra, not geometry, but basic topology. ”But the union might be infinite, therefore not necessarily closed!” I wanted to tackle a greater problem, but I’m stuck with administrative bullshit within administrative bullshit. I hate this lemma. Just make it end please. i can’t take this anymore. Help.... Please, for the love of God, give me an admin assistant. I just want someone to take care of me at this point. This is frustrating and I’m tired of working. I can’t do it. I give up. I I just want someone to treat me like a child for a week. I’m not joking. Just do everything for me for a week or two and let me relax, make me relax. Handle this stupid, dirty work. Take care of my stupid finances. God. Someone handle me right now. Please, someone princess-carry me to bed. I’m serious. I can’t take this anymore. Just for a week, please. Maybe 2 weeks. Feed me soup and tuck me in. At least kiss my peni Anyway, here’s a proof I don’t undertand.

QED

 

A

 

By the way, is it comical that I skipped such a ”fundamental” exercise? My head is all over the place: Hartshorne rarely gives us the forest, only the trees. So we shall work on tree-to-tree basis.

 

We want to show that if f is a closed immersion, then f′ is a closed immersion.

With our lemma 0.0.2 proven, all in 2 can be assumed to be affine, thus giving us a contravariant algebraic diagram:

The problem now reduces to showing that if f is surjective, then f′ is surjective. Since f(A) = B, by definition of p₁ we have

{b ⊗ 1|b ∈ B}	= p1(B)
	= p1(f(A))
	= (p1 ∘ f)(A)
	= (f′∘ g)(A)
	= f′(g(A))

 


So f′ can reach all the b⊗ 1 through the image of g(A). But I also know that f′ can reach all the 1 ⊗ a′ by definition of the tensor product. So in total, it can reach all the b ⊗ a′, i.e. all the basis elements. It reaches all of B ⊗_AA′. Done.

C

 

At the affine level, making subscheme structures on closed sets is easy:



The reduced induced structure is the smallest of these structures (glued together):



Ofc, the fact that it is the ”smallest” is what we’re showing here. Categorically: ”Smallest” means that it factors thru all other subscheme structures on it.

It’s initial. It’s a universal property baby. It’s easy to see that things glue here, so we can reduce to affines:

Algebraically,

And the existence of the dashed morphism is obvious, since α ⊃ α′, by construction. Done.

In fact, with α being the ”intersection of all the prime ideals” containing the closed set, I know that α = . It is the radical of any other ideal that gives the same closed set. In other words,

0.0.3 Lemma

SpecA∕α is has the reduced induced structure ⇔ α is radical.

0.0.4 Trivial. QED

 

D

 

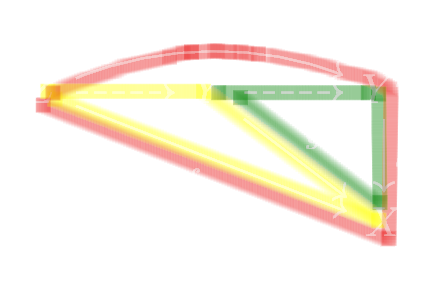
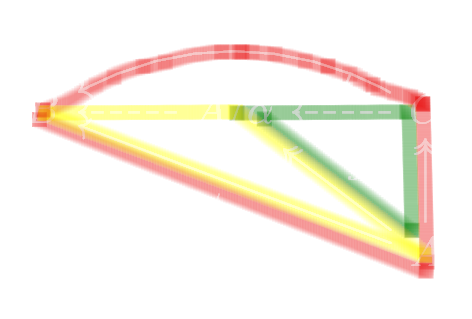
This is an extremely wordy explanation, so let’s draw it in diagrams.

0.0.5 The clean-shaven painter

Let us outline our master commutative diagram, for this part:

 

Y ′→ X is a an arbitrary closed subscheme (a closed immersion), and Y → X is a closed subscheme we are constructing. Let’s paint it:

 

This exercise asks us to find the unique closed subscheme Y → X such that we get red, and given yellow, we get green.

0.0.6 Getting red

Let’s attempt to construct Y . And taking a hint from Hartshorne, let’s set Y = f(Z) as a set. And note, given an open cover Y = ⋃ _iV _i,  

f(Z)	= f(Z) ∩ Y
	= f(Z) ∩⋃ iV i
	= ⋃ if(Z) ∩ V i
	= ⋃ if(Z) ∩ V i

 


CAREFUL: That overline signifies the closure of f(Z) in Y . Let’s be more specific:

clY (f(Z)) ∩ V i

= clV i(f(Z) ∩ V i)

 


Which is, simply, the closure of the restriction of f to f⁻¹(V _i) → V _i. So we can reduce to affines. We are looking at a morphism

 


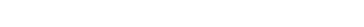which is induced by a morphism

 


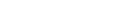And we let Y = f(Z) ⊂ X. Hence, we have a commutative diagram.

Now, of course, this begs the question: What is Y = f(Z) in the perspective of this affine world? Well, it is a closed subset of SpecA, so what closed subscheme structure should we give it? Presumably, f(Z) = V (α) for some ideal α in A. What is α?


Well, we’re trying to catch f(Z). We want the image of Z = SpecB. I.e. we want the union of f(P) = ϕ⁻¹(P) for all the P ∈ SpecB. And V (α) is all the prime ideals that contain α. So what’s a α that all the ϕ⁻¹(P)’s contain, without leaving room for too many extra ideals? (of course, we can leave some room for extra ideals, because we’re catching f(Z), not f(Z)). Well, why not just intersect em all?

 


Huh? Is this even an ideal? Of course it is. Let

 


be the nilradical of B. It is a (proper) ideal, so ϕ⁻¹(𝒩_B) is an ideal. But

 


So ϕ⁻¹(𝒩_B) = α. Hence α is an ideal


Again, our goal is to verify this equality:

 


So let P ∈f(Z). Now suppose P V (α), which means that P is in the open neighborhood U = X − V (α). And since P ∈f(Z), we have that

 


I.e. there is a Q ∈ Z such that f(Q) ∈ U. And

f(Q) ∈ U
f(Q) V (α)
f(Q)⊅α

 


Which contradicts the definition of α. Hence f(Z) ⊂ V (α). Now for the reverse inclusion.


Let P ∈ V (α), so P ⊃ α. Now suppose P f(Z). I.e. there is an open neighborhood D(x) ∋ P such that

 


Then for all Q ∈ Z, we’d have that f(Q) D(x). i.e. f(Q) ∈ V (x). i.e.

∀Q ∈ Z : f(Q) ∋ x
⋂ Q∈SpecBf(Q) ∋ x
α ∋ x
P ∋ x

 


which contradicts P ∈ D(x). Hence, f(Z) ⊃ V (α). So f(Z) = V (α). In which case, 5 turns into

This all works out as set maps for obvious reasons, but to verify that this diagrams works as morphisms of schemes, we need

 

And I shall construct δ in the manner that I am practically forced to. Wait, doesn’t this sound familiar?

δ : A∕α	→ B
[x]	ϕ(x)

 


And we have to verify that it is well defined...

[x]	= [y]
x − y	∈ α
	= ϕ−1( )
ϕ(x − y)	∈
∃n > 0 : (ϕ(x − y))n	= 0

 


And here we are, at a crucial point: To finish this off, I need to assume Z = SpecB is reduced. In which case, I can write

ϕ(x − y)	= 0
ϕ(x)	= ϕ(y)

 


Thus allowing the map to be well-defined. And since we are assuming Z is reduced, let’s check if we got the reduced induced structure on Y , i.e. that = α (i.e. α is radical):

xn	∈ α
ϕ(xn)	∈
	= (0)	(B reduced)
ϕ(xn)	= 0
ϕ(x)n	= 0
ϕ(x)	= 0	(B reduced)
x	∈ ϕ−1((0))
	= ϕ−1( )
	= α

 


So α is radical, and Y has the reduced induced structure.

0.0.7 yellow and green

Now that everything is affine, let’s verify all the properties check out, (with the extra assumption that Z is reduced). Recall our drawing:

Which I shall now adapt algebraically. Ysee, since Y ′→ X is a closed immersion, its corresponding ring morphism is surjective. And thus, given my construction of Y , the corresponding diagram is

I.e. the problem is now the following painting:

GEOMETRY REDUCED TO ALGEBRA. AHHH, THE RING O’ HARTSHORNED: I want to show that A∕α is a ring such that we get red (which I already have), and given yellow, we get green. Now thanks to the surjectivity of h, the definition of g′ is forced by g. Since g determines ϕ, which determines l, it all commutes. The uniqueness of A∕α follows from C since Z, i.e. B is reduced. See figure 1.

0.0.8 If Z is not reduced?

Let’s bring up our drawing again:

If Z is not reduced, then my construction for Y doesn’t work, so that dashed uncertainty remains dashed and uncertain. Now, there is a version of Z that is reduced: Z_red, as introduced in 2.3B. And if I had a morphism Z → Z_red, I can construct Y from Z_red and factor through it:

This diagram would, more or less, complete the proof. Of course, we do not have this situation, because we do not have a morphism Z → Z_red. In 2.3B, we constructed the opposite: A morphism Z_red → Z, induced naturally from A → A∕ . If we wanted a morphism from Z → Z_red, we’d have to make a morphism

 


Which is infeasible.























...Solution time? There are none. Everyone skips this part or gets it incorrect. I’m not joking:

And, finally:



And thus, onto section 5.