SOLDIERS: Youve slaved away at this siege for a nontrivial length of time. Youve no clothes, no food, no ammo. Your heads are stuck in the trenches of fundamentals, the mire of coastal artillery. Youve been stuck under a poor show of leadership. Youre underappreciated, scolded for things that arent your fault. They billet back in Ol’ Oll, while you’re holding down the redoubts, pitting your flimsy batteries against red-and-gold naval first-rates in exhausting 7hour gunduels. And they still have the audacity to come upon you and scold you, and nitpick at you, and ask you to ”stop complaining.” Hah! They give you orders without direction. Sans culottes sans fire. Never felt the whizz of roundshot, the WHACK of grapeshot. Theyve given you no path for success, no progress. And they still have the audacity to talk down at you, to get angry at you for the stalling of this siege. No guidance. Explanations without tests. They hold back the details then blame you for the devil. The man ranked above us isn’t one cut above us, distant yet present. He is secluded from your circmustances, living almost in another world like an alien. They call you incompetent for not knowing how to do simple things, when no one had ever taught you. They provide no overall trajectory to hold you against, just daily tasks they can moodily spit on you over. They think morale should just generate itself. They think you’re fickle when you’re just stuck. Out of sleep—out of fear—out of whack. Christ, I’ve been dreaming about reloading cannons. Sometimes I’m doing nothing and I notice my hands going through the motions. I’ve had enough artillery for a lifetime. I’m sure yall have too. My mind is so full of artillery formations and information I’m going insane. I understand: If this led anywhere, you’d be all in, but we aren’t being led–we’re being held. Siege or no siege, that’s the truth of life for most people. When life goes day by day, moment by moment, as if there were no larger strategy to the whole affair—it is that philosophical focus on tactics which kills morale. Just live in the moment! OooOOoo ← and then you’re dead. Not very convincing, is it? Come on now. Do you fear death? People say things like ”Death is merely nonexistence–the absence of existence” then run like pussies when they’re in actual danger. Focus, boys. What are you truly hungry for? In the worst case, you’re at least smart enough to fake it. Yes, I’ve sermoned on how mere nominalization blows an object up in importance, regardless of its substantive qualities. Names are weapons. The pen and sword go hand in hand. And Clausewitzian continuity applies here: If you don’t use it, you lose it. Parisians forgot how fire #86 was.


SOLDIERS: You are cleverer than they think. You aren’t educated in the traditional sense. Some of yall can’t even read. But you’ve demonstrated the ability to unspike a cannon. Some of you’ve mastered the dangerous art of mortars. You can all banter under fire. You will listen as long as you have direction. And you’ve been listening. Despite how the higherups like to assume the heart and soul of strategy doesn’t trickle down, you’ve been squeezing every drop of information you can get, rather than idling by your battery in downtime. You’ve hounded me for what I know: who’s doing what, who said this, what’s the newest dumbass plan they came up with. Against all odds, you’re not in the dark. You’ve shined light on yourselves. And yes, you’ve been watching. I concretely demonstrated my theoretical sermons on naming. You watched it go: OF THE MOUNTAIN; BREECHLESS BRIGADIERS; SABLETTES; BREGAURT; QUATRE MOULINS–how men flocked to their favorite names. And you’ve followed suit: You heard about the jutting into the Rade of the Eguillette, how mastering it means mastering the harbor, and you’ve correctly given it a cute nickname. It worked. But it fades in the confusion, the indecisiveness of our superiors–the effect wanes day by day, week by week. Sans clothes, sans good, sans ammo. Trees of cannons hidden underneath a mire. Where is this red coastal forest pointed to admist our quagtrees? If you don’t use it, you lose it. Bring your attention back to that jut. Every battery serves as either a feint to distract the enemy from that jut, or a direct assault on that point. Everything comes back to that jut. Memorize that into your gut. And thus, here’s another cute name for yall.

5

 


And we are at the final stretch of fundamentals. According to Schoolmaster Hartshorne, this is the last of the sections in this chapter establishing ”grounding.” Yall are tired. Our wings begging to be bared. Our dicks are hard. What wondrous adventures lies beyond this hurdle is up to the imagination. But we have some more foundation to construct–some foundation that gives us a taste of freedom. You thought structure sheaves brought freedom? What about sheaves over structure sheaves?




The zoo of sheaves is back to adorn our zoo of schemes. We’re getting into the hardcore ”fundamentals” now. If you wanna spread your wings, you have to shed fear. Donut be scared. I’m right here with you, holding your hand. So when I screw up, so will you. Ha ha ha ha ha.

5.1

 

A (locally) free sheaf of modules is defined somewhat naturally:



As is the construction that goes by ”sheaf Hom”:



The point of this exercise is that locally free sheaves act nicely.

A

 

HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA HAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA


When I screw up, so will you. So hold on tight. We want to show this:

 


Now, watch this. Let U be an open that makes ℰ free over 𝒪_X. By that I mean,

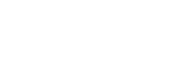(1)

 


For some fixed finite n that doesn’t depend on U (since it’s fixed rank). Hence for the purposes of this exercise, I’ll just write

 


for simplicity, with the understanding that there’s a fixed finite number of copies in the direct sum.


Before we go ahead and evaluate the dual of the dual ((ℰ)^ˇ )^ˇ, let’s just evaluate the plain old dual (ℰ)^ˇ. In which case,

(ℰ)ˇ	= ℋom 𝒪X(ℰ,𝒪X)
(ℰ)ˇ(U)	= ℋom 𝒪X(ℰ,𝒪X)(U)
	= Hom𝒪X|U(ℰ|U,𝒪X|U)
	= Hom𝒪X|U(⊕ 𝒪X|U,𝒪X|U)	(by (1))

 


Just think about this last expression. Let’s say f ∈ (ℰ)^ˇ(U), so that

 


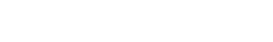is a morphism of sheaves of modules over 𝒪_X|_U. In that case, given open W ⊂ U, we have

f(W) : ⊕ 𝒪X|U(W)	→𝒪X|U(W)	(2)
i.e. f(W) : ⊕ 𝒪X(W)	→𝒪X(W)	(3)
		(4)

 


Now, let’s just think about this situation philosophically, shall we?

0.0.1 Lemma

Let M be an R-module. Then

 


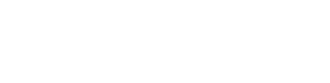By the way, I’ll also start using the notation Rⁿ = ⊕ _i=1ⁿR for the finite direct sum.

Proof

Let r = (r₁,…,r_n) ∈ Rⁿ, let e₁ = (1, 0, 0,…0), and e₂ = (0, 1, 0,…, 0), etc.). Then

r	= (r1,…rn)
	= (r1, 0, 0,…, 0) + (0,r2, 0,…, 0) + + (0, 0, 0,…,rn)
	= r1(1, 0, 0,…, 0) + r2(0, 1, 0,…, 0) + + rn(0, 0, 0,…, 1)
	= r1e1 + r2e3 + rnen

 


Let f : ⊕ _i=1ⁿR → M. Then

f(r)	= f(r1e1 + + rnen)
	= f(r1e1) + + f(rnen)
	= r1f(e1) + + rnf(en)

 


Which means that f is fully determined by where it sends the ”standard basis elements” e₁,…,e_n to M. I.e. f effectively selects n elements from M that can be linearly combined over R. I.e. f is just an element of⊕ _i=1ⁿM

QED

 

Now, what does this entail? When we selected f ∈ Hom_𝒪X|U(⊕ 𝒪_X|_U,𝒪_X|_U), and grabbed its sections over W, (3) tells us that f(W) ∈ Hom_𝒪X(W)(⊕ 𝒪_X(W),𝒪_X(W)) which according to the lemma, simply means that

 


So given W open in U, f selects n basis elements from 𝒪_XW.


But I can do even better. f is a morphism of sheaves, so it has to be consistent along restrictions:  

 

The map on the left sends basis elements to basis elements. Hence, f(W) is completely determined by the map of global sections f(U). So i can ignoreall the nonglobal sections and just write

 


But ⊕ 𝒪_X(U) ≃ℰ(U), and f was an arbitrary element of (ℰ)^ˇ(U), so (ℰ)^ˇ(U) ≃ℰ(U). And therefore....

(5)

 


.......


WHAT!?

0.1 Two Levers

 


OUT OF FEAR, HE SAYS. Peur. I, poor soul, followed the exact same path as this poor fool, and look where it led me. The fearful all fall into the same hole. THE FOLLY OF FEAR MAKES US FALL. I, like this fellow (And I like this fellow, indeed), was following the example of many algebraic geometers who put glueing aside as a trivial task. But we have to be more careful, because this guy who calls himself ”Evariste” is wrong.  





Yeah... I should add to my sermons that naming should be done with restraint. Don’t be too quick to name yourself after a genius mathematician. In any case, like ”Evariste,” I presumed that, after creating (iso)morphisms g_U : ℰ(U) → (ℰ)^ˇ(U), on an open cover of X, that would glue to an (iso)morphism ℰ→ (ℰ)^ˇ. This is, of course, an incorrect assumption: Morphisms of local sections do not always glue into a morphism of sheaves. To really see the issue, let’s try defining a morphism ϕ : ℰ→ (ℰ)^ˇ, which means, in general, we’d need, for an arbitrary open set U,

ϕ(U) : ℰ(U)	→ℋom(ℰ,𝒪X)(U)
i.e.ϕ(U) : ℰ(U)	→ℋom(ℰ|U,𝒪X|U)

 


So, given s ∈ℰ(U), I need to send it to a morphism

f : ℰ|U	→𝒪X|U
f(W) : ℰ(W)	→𝒪X(W)

 


Is there any obvious way to do this in general? No. It’s only when ℰ(W) happens to be a free module over 𝒪_X(W) that a natural definition arises. But there are many more open sets in X and the ”natural” definitions on the free W’s don’t necessarily glue together correctly on those sets. (5) is wrong in general.

A: Attempt 2

 

SOMETIMES LOOOOVE COMES AROUND, AND IT KNOCKS YOU DOWN. JUST GET BACK UP WHEN IT KNOCKS YOU DOWN. Let’s give this another shot. Again, our goal is to show

 


And the approach we’re going to take is to construct a morphism

ϕ : ℰ	→ ((ℰ)ˇ )ˇ
i.e.ϕ : ℰ	→ℋom𝒪X((ℰ)ˇ ,𝒪 X)
i.e.ϕ : ℰ	→ℋom𝒪X(ℋom𝒪X(ℰ,𝒪X),𝒪X)

 


So, for any open set U, we need to define

ϕ(U) : ℰ(U)	→ℋom𝒪X(ℋom𝒪X(ℰ,𝒪X),𝒪X)(U)
i.e.ϕ(U) : ℰ(U)	→ Hom𝒪X|U(ℋom𝒪X(ℰ,𝒪X)|U,𝒪X|U)(U)

 


So given s ∈ℰ(U), I have to map it to a morphism of 𝒪_X

 


so for an open set W ⊂ X, I need to define

 


so given g : ℰ|_W →𝒪_X|_W, the most natural place to send it to is

 


That gives a definition of ϕ: I send s to the map that evaluates everything in (ℰ)^ˇ at s, restricted appropriately (”restricted appropriately” - hence, it is indeed a morphism of sheaves, unlike the failed glueing I attempted earlier).

On stalks, ϕ becomes

 


And on the stalk level, it is true that ℰ_P = ⊕ 𝒪_P,X. We are in the category of 𝒪_P,X-modules (actual modules, not sheaves over modules). And thus now we can apply lemma 0.0.1 from earlier to claim that ϕ_P is an isomorphism. Done

B

 

Finally, a new part. And, another isomorphism to prove:

 


i.e.

 


And a new(ish) concept: Tensor products of sheaves over modules:



Which I will do like so:

δ(U) : Hom𝒪X|U(ℰ|U,𝒪X|U) ⊗𝒪X(U)ℱ(U)	→ Hom𝒪X|U(ℰ|U,ℱ|U)
f ⊗ x	x ⋅ f

 


NOTE THAT THIS IS A MORPHISM OF PRE-SHEAVES. The tensor product is the sheaf associated to the presheaf given by the LHS


But that’s fine, because of how sheafification works:



Two important notes in the picture above. First, I can induce ϕ through δ:



And secondly, sheafifcation preserves stalks. So our definition of δ translates naturally to ϕ on the stalk level:

ϕP : Hom𝒪P,X(ℰP,𝒪P,X) ⊗𝒪P,XℱP	→ Hom𝒪P,X(ℰP,ℱP)	(6)
fP ⊗ xP	xP ⋅ fP	(7)

 


So no more worrying about sheafification. We just need to show that the above is an isomorphism. We have ℰ_P ≃⊕ 𝒪_P,X. Hence (6) turns into...

ϕP : Hom𝒪P,X(⊕ 𝒪P,X,𝒪P,X) ⊗𝒪P,XℱP	→ Hom𝒪P,X(⊕ 𝒪P,X,ℱP)
i.e. ϕp : (⊕ 𝒪P,X) ⊗𝒪P,XℱP	→⊕ ℱP	(Lemma 0.0.1)
i.e. ϕP : ⊕ (𝒪P,X ⊗𝒪P,XℱP)	→⊕ ℱP	(Tensor and direct sum commute)
i.e. ϕP : ⊕ ℱP	→⊕ ℱP

 


which is clearly an isomorphism

C

 

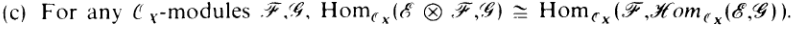
Another isomorphism, and THIS ONE in particular may look familiar to certain mathematicians.

(8)

 


Heh heh heh. First of all, take a look at the fact that this is Hom, not ℋom. We just need a bijection (of morphisms of sheaves), not a morphism of sheaves. But since morphisms of sheaves are defined according to open sets, let’s beg a tempting question:

(9)

 


Now we’re talking about a bijection of morphisms of modules over rings. You see it?

 

I will skim over the headache that are the sheafification and glueing details: A morphism on the left hand side of (8) can be broken up into its open set components and be induced thru sheafification from an element in the LHS of (8) (HMMM. Can we associate morphisms of sheaves with morphisms of presheaves, like we can vice-versa?), then get sent bijectively onto the RHS of (9) (HMMM. We’re assuming they glue together back up to the RHS of (8). EXERCISE LEFT TO READER)

D

 

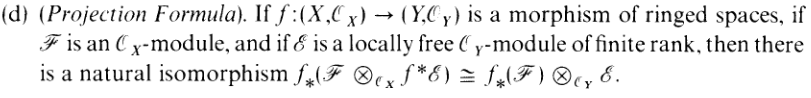
And another isomorphism. This time it’s

(10)

 


where f_∗ and f^∗ is given by the following sequence of definitions




Now (10) looks like utter nonsense, and indeed I spent quite some time chasing this isomorphism down futilely, until I realized what this isomorphism is really saying. It’s a statement about commutativity. Here’s what we would like to do:

f∗(ℱ⊗𝒪Xf∗ℰ)	= f ∗(ℱ) ⊗f∗(𝒪X)f∗(f∗ℰ)
	= f∗(ℱ) ⊗𝒪Y f∗f∗ℰ
	= f∗(ℱ) ⊗𝒪Y ℰ

 


Each of those equalities can be dealt with in a separate lemma. And that is what I shall do. Starting with...

0.1.1 Lemma: Direct image commutes with direct sum

Let f : (X,𝒪_X) → (Y,𝒪_Y ) be a morphism of ringed spaces, and let ℱ,𝒢 be 𝒪_X-modules. Then

 

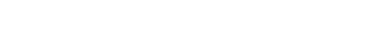Proof

Let’s consider the tensor products as presheaves. Then given V open in Y ,

f∗(ℱ⊗𝒪X𝒢)(V )	= (ℱ⊗𝒪X𝒢)(f−1(V ))
	= ℱ(f−1(V )) ⊗ 𝒪X(f−1(V ))𝒢(f−1(V ))
	= f∗(ℱ(V )) ⊗f∗(𝒪X(V ))f∗(𝒢(V ))
	= (f∗ℱ⊗f∗𝒪Xf∗𝒢)(V )

 


So the presheaf tensor products are isomorphic. And this isomorphism induces an isomorphism of the sheafified tensor products proper (because they’re isomorphic on the stalks).

QED

 

0.1.2 Lemma

Let f : (X,𝒪_X) → (Y,𝒪_Y ) be a morphism of ringed spaces again. And this time let ℱ′,𝒢′ be 𝒪_Y -modules. then.

 

Proof

Since f : (X,𝒪_X) → (Y,𝒪_Y ) is a map of ringed spaces, it induces a map

 


WHICH I REALIZE I HAVE ACCIDENTALLY BEEN WRITING THROUGHOUT THIS CHAPTER AS 𝒪_Y →𝒪_X, SORRY. YOU KNOW WHAT I MEANT. Hence we have the following commutative diagram:



The top diamond is the universal property of f_∗ℱ⊗_f∗𝒪Xf_∗𝒢, but with the dashed arrow on the bottom, f_∗ℱ⊗_f∗𝒪Xf_∗𝒢 also satisfies the universal property of f_∗ℱ⊗_𝒪Y f_∗𝒢. Hence they are isomorphic.

QED

 

And, for the final piece:

0.1.3 Lemma

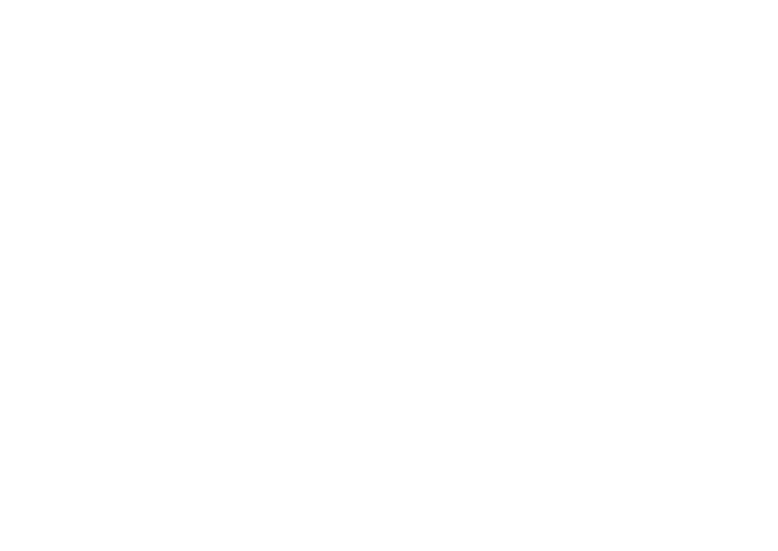
Let f : (X,𝒪_X) → (Y,𝒪_Y ) be a morphism of ringed spaces, and let ℰ be a locally free 𝒪_Y -module of finite rank. Then

 

Proof

First of all, applying the definition of f^∗ and lemma 0.1.1

f∗f∗ℰ	= f ∗(f−1ℰ⊗ f−1𝒪Y 𝒪X)	(11)
	= f∗f−1ℰ⊗ f∗f−1𝒪Y f∗𝒪X	(12)
		(13)

 


And, thank goodness, I did 1.18, developing the adjointness of f_∗ ’gainst f⁻¹. Indeed, right here I defined a map

ψ : 𝒢	→ f∗f−1𝒢			(14)
ψ(V ) : 𝒢(V )	→ f∗f−1𝒢(V )	(V ⊂ Y open)		(15)
s	< V,s >			(16)

 


SHE HANGS. In the case of 𝒢 = ℰ, this is a bijection because of the same argument I made earlier in this post regarding direct sum restrictions. So we have f_∗f⁻¹ℰ = ℰ, and thus (12) reduces down to

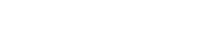(17)

 


And now using (14) again, note that the following diagram commutes



Hence, by universal properties, I can reduce (17) to

(18)

 


And now, one more commutative diagram to finish the job



I am simply factoring the right hand side through 𝒪_Y , to emphasize that ℰ⊗_𝒪Y f_∗𝒪_X in fact satisfies the universal property of ℰ⊗_𝒪Y 𝒪_Y . Hence (18) reduces to

(19)

 


And since ℰ is a 𝒪_Y -module,

(20)

 

QED

 

And we are done with five point one.