II.1.18
12/31/2021
a a a a AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
FDHOHAOHSOAFOAJWWOAFOAHFPWAHFPWAPAHPFHWAPFHPWAHFPWAHFPAHFPAWFPWAPFWAHPFHWAPFHWPAHPWAFHPAHUFPWAUFPAFPWAUPWAFWAFAPFWAFWAFDAFPWAHFWHFPWTPWAHTPWATPWAJPAJFJCAPSNJCAPJVSSAJWASPSAVNHANVPWNVGPA
WITH YOUR HEAD HELD HIGH AND YOUR SCARLET
LIIIIES YOU CAME DOWN TO ME FROM THE OPEN SKIIIIES
What the fuck is an adjoint functor. I ate two full bars of dark chocolate.... Two... Full... Bars...
M-muh tummy... Softly... Gently... You're a slick little fellow, aren't ya? Hold me... I'm wasting my 20s. . DATABASE DATABASE DATABASE DATABASE
DATABASE DATABASE DATABASE DATABASE DATABASE DATABASE
DATABASE DATABASE DATABASE JIBUN WOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO
She hangs. Threads threaded through her veins and out of her soles, then
joined bare some paces and finally tied to the chandelier, from which candlewax
dripping and following the curves and paths and arches, finds its way
down to the central nipple pointed down, trailing down that bundle of
threads like raindrops on a car window and thinning it little by little by
She hangs, crucified upsidedown like a bat, arms spread like arms, and
the sleeves of her blouse like wingfilm, breeze through open windows speaking
through flimflam filmflap. Laid up and swung out and strung down. Deathly
dangling, dark circumferences of socket holding ballish greening eyes. Swinging to,
fro, to, fro, implicitly shouting for Mama Wind to push, and that classic
coincidence of apathetic nature generously responding to unnatural call.
Her shadow hangs on the Western Wall, innocence swindled. Urine yanked
out. Unrivaled. She hangs, dead center in the room, woman of the hour. A statue
towering from above, a ceiling mural reaching out into the room and scooping out
reality. Prorated and forever contemporary. She is wading in the air; a freeform
pendulum counting something unknown. A private countdown as the year reaches
its own end.
She hangs ahoy, ankles shackled and head lifted from the Earth. Pulled out
like an onion and partly peeled back. A treasure chest sprung out of the shore.
Skin picked and shedding like sand. Decaying in dim shapes of light and
shadow, dignity pillaged, risen above mundanity yet forever faithful to it.
She hangs yes she does tither, hither, like an inverted rocking horse, left-right
orientation matching the face-to-face voyeur. Cadaverous inversion to straight life,
whence true love. Spoilt love. That bloody, roachy corpse comfortably
exposed as if mummified, as if protected from public view by a gently
rocking warm cocoon, as if paused in the middle of some transformation
whose intermediate steps are as grotesque as the finale is surely beautiful.
She hangs, hair sickly, coming off. Half a nostril missing. Tongue licking
upper lip. Grayfaced youth, arms squandered, sinking more trying to reach the
depths beyond the sullied floor indeed to fly down into deep heights never reached
before if not to collapse into a intestinal voodoo-jointed mess upon hitting
the floor when the last thread loses its grip. And under crusty forehead
caved in cheeks through caustic lips, dead but alive, a voice within a
voice sounds: some alien kernel within speaking out of that thin hole:

Now, murid has a point, but have they considered that the years are actually
getting BETTER? 2019 was much like a dark void for everyone. But in 2020,
COVID-19 hit and brought peace and joy onto the world. Then in 2021,
COVID-19 was so popular and well-loved that it decided to go for Round 2,
further decreasing political and cultural divisions and bringing us closer and more
physically intimate than ever before. It was the unification we had always been
waiting for. Brother hugging brother, sister embracing sister, neighbors
joining hands, and looking upon a utopic economy that...
DSHDHSHFDHSFOAFJPWJPAWAFWAIFPAFGAIFPWAIFPAUPRATPWAITWPAJPAVPJVWPBWAPBMAPWBKAWAWBJPAJBPWAJBVPAJWBPAJBPAWKPAKBVPAWBVPAPVGWAGPAWFPWAFJOAJFDWIAJIWAJDAIJAWJDAJDWAJDIWJWIJDIWJAIJWJAIJWIJIAJWJGIGIRIRGIRIRKLGRIGRLRGI
It's 2022. Listen: I see a lot of grimposting going around the net. I see all
the depression and misery and loss of hope. But you gotta stay calm.
Even if everything goes down in flames, you have to keep chugging.
Turn on Pyrovision if you must.
Just get it done. "Excellent advice, holeinmyheart. This is exactly why I
come to this blog. For all your extremely concrete, motivational advice."
SO, today's exercise is about a particular pair of adjoint functors! We used one of
em last time, but here they are again for good measure:

So this exercise should be "easy" because all the maps are "natural". YAAAY. So
if we just roll through the definitions, the maps should "make themselves."
1 Left on right
Let's try and figure out
 |
To define ϕ, I need to define, for every open set U ⊂ X,
 | (1) |
Then simply reading out the definitions above, I can unwrap the lhs as
f-1f
*
 (U) (U) | = lim V ⊃f(U)f*
 (V ) (V ) | ||
= lim V ⊃f(U)
 (f-1(V )) (f-1(V )) |
So (2) is
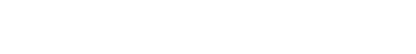 | (2) |
ALRIGHT, THAT LEFT HAND SIDE LOOKS MESSY AS HELL. Let's denote
the restriction maps of f-1f*
 as ρ′. And the restriction maps of f*
as ρ′. And the restriction maps of f*
 and
and
 as ρ (denoting them the same since the former inherits the latter). The question
is: What to elements in the left set looks like? It's a direct limit, so they look like
this:
as ρ (denoting them the same since the former inherits the latter). The question
is: What to elements in the left set looks like? It's a direct limit, so they look like
this:
| < V,s > | s.t. V ⊃ f(U),s ∈
 (f-1(V )) (f-1(V )) |
with the equivalence relation
| < V,s > | ~< W,t > | (3) |
| ⇔∃T ⊃ f(U) : ρ′V,T(s) | = ρ′W,T(t) | (4) |
| i.e.ρf-1(V ),f-1(T)(s) | = ρf-1(W),f-1(T)(t) | (5) |
"Dude, what the fuck is this shit"
I...It makes sense if you think abt it.... The equivalence relation is: GIVEN AN
OPEN SUPERSET OF f(U) ⊂ Y (since f(U) isn't guaranteed to be open
itself), PULL BACK TO AN OPEN SET IN X, RESTRICT, AND COMPARE.
Now, the major insight here as far as defining ϕ(U) is that s ∈
 (f-1(V )),
and
(f-1(V )),
and
| f-1(V ) | ⊃ f-1(f(U)) | ||
| ⊃ U |
So we can restrict s to an element of
 (U). HENCE, THE
NATURALLLLL DEFINITION OF OUR MAP
IS
(U). HENCE, THE
NATURALLLLL DEFINITION OF OUR MAP
IS
| < V,s > |
 ρf-1(V ),U(s) ρf-1(V ),U(s) |
"Alright, great. Now, is this map well-defined?"
Ha... Hahaha... Hahahahaha... Mua.. Muahahaha.
MUAHAHAHAHAHAHAHAHA. MUAHAHAHAHAHAHAHAHAHAHAH.
MUAHAHAHAHAHAHAHAHAHAHHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHA.
MUAHAHAHAHAHHAAHAHAAAAAAAAAHAHA AHAHAHHHHHHHAHAAAAAAAH
HAAAAAAAAAAAAAAAAAAAAAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAHAH
1.1 Cute and valid?
Answer: FUCK IF I KNOW. Well, okay, I actually DO KNOW that it IS... But I
CAN'T PROVE IT!!! Look:
| ϕ(< V,s >) | = ϕ(< W,t >) | ||
 ρf-1(V ),U(s) ρf-1(V ),U(s) | = ρf-1(W),U(s) |
With this info, I'm supposed to prove the equality
| < V,s > |
 < W,t > < W,t > |
holds, right? WELL..... I CAN'T. Because in order for that equality to
hold, looking back at (5), I need some set T ⊃ f(U) in Y such that
| ρf-1(V ),f-1(T)(s) | = ρf-1(T),f-1(T)(s) |
Now, look... I know when restricted to U, s = t, but every set f-1(T)
contains U, and in particular may not equal U. I need a set larger than U in
which s = t (and furthermore is inversely mapped onto from an open set in Y )....
HOW THE FUCK?
I'm moving on
2 Right on Left
Okay, this one is less of a pain in the butt. We want a NATCHURAL map
 |
I.e. we need to make, given open V ⊂ Y ,
 |
So the side that's needs to be unraveled this time is the RHS:
f*f-1
 (V ) (V ) | = f-1
 (f-1(V )) (f-1(V )) | ||
= lim W⊃f(f-1(V ))
 (W) (W) |
Okay, the key point here is V itself is one of those Ws, since V ⊃ f(f-1(V )),
so our map can obviously just be
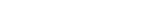 |
NO CUTE AND VALID CHECK NEEDED. YAY.
3 The moment you've all been waiting for: Adjointness
Alright, I need a NATCHURAL bijection
 |
Okay, what I decided to do after getting brainfucked trying to think about this
was, let's break it up. Start with the simpler problem:
3.1 my new creation: the f* operator on morphisms
Let's say
 ,
,
 , are sheaves on X, f : X → Y is continuous, and suppose
h :
, are sheaves on X, f : X → Y is continuous, and suppose
h :
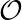 →
→ . I would like to induce a map
. I would like to induce a map
 |
i.e. for any open set V ⊂ Y , I need to define
f*h(V ) : f*
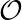 (V ) (V ) | → f*
 (V ) (V ) | ||
i.e. f*h(V ) :
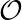 (f-1(V )) (f-1(V )) | →
 (f-1(V )) (f-1(V )) |
at which point, the definition becomes obvious (NATURAL!):
| f*h(V ) | = h(f-1(V )) |
3.2 inducing le map using the f* operator
So, basically, now given h ∈ HomX(f-1
 ,
,
 ), i.e.
), i.e.
h : f-1
 | →
 |
I can induce a map
f*h : f*f-1
 | → f
*
 |
and NOW to get the desired element of HomY (
 ,f*
,f*
 ) all I have to do is
right compose with the previously created ψ. Behold:
) all I have to do is
right compose with the previously created ψ. Behold:
"......................................................"
Err... yea. I tried to use tikz-cd, and as you can see, tex4ht did not respond well
do that...
Here, I'll give you the screenshot from my editor instead:

3.3 The f-1 operator
Since I'm making a bijection, I'd like to make a map in the opposite direction.
So...
Let
 ,
,
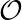 be sheaves on Y , and f : X → Y a cont map, and let h :
be sheaves on Y , and f : X → Y a cont map, and let h :
 →
→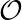 .
Now I want to define a map
.
Now I want to define a map
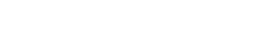 |
i.e. given open U ⊂ X, I'd like to make
f-1h(U) : f-1
 (U) (U) | → f-1
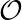 (U) (U) | ||
i.e.f-1h(U) : lim
V ⊃f(U)
 (V ) (V ) | → lim W⊃f(U)
 (W) (W) |
so the "obvious" NAAATURAL map is just
| f-1h(U)(< V,s >) | =< V,h(V )(s) > |
3.3.1 cute and valid?
Fuck you, I'm not checking
3.4 Inducing the inverse map using f-1
Now given h :
 → f*
→ f*
 , I can induce a map
, I can induce a map
f-1h : f-1
 | → f-1f
*
 |
and then get the desired map by left composing with ϕ from above:

oofff.. that ain't it bros... that ain't it....
Well, here's a screenshot again of what it was SUPPOSED to be:
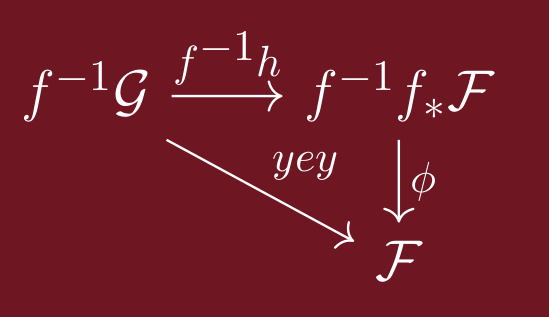
Done
3.5 Happy new year
Now we have to verify that we made a bijection; that yey maps to yay
and viceversa. Seems like quite a pain. But the more you look, as all
"natural" things are, it's borderline computational. The problem shall solve
itself as long as you follow the path. Walk, and the contructions should
construct themselves. Carry yourself by your ideal visions of yourself and
fall unconsciously into the bliss of being, as the world collapses around
you.
When the skies are dark, it enables you to cut out the extraneous stuff. It enables
you to harvest that tinge of evil in you. You know what you have to do and
why. You've known it for years. It's been inside you as long as you can
remember.
Now's the year. All you have to do is keep your eyes on the prize and you'll be
unstoppable. I know you can do this. Hence,
EXERCISE LEFT TO READER
Welcome to 2022. It's here, whether you like it or not.