WELCOME TO 2022!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Is this how you want to start 2022, Mr. holeinmyheart? Spam? Is this how you would like to punctutate the turn of the year? Hah! An opportunity to welcome these three twos and one zero, and you squander it with a wallop of crude spam! Disgusting! Defeatist, self-hating laughter! Laughing and typing in tables of style over substance. Dress'd in ironplated irony, estranged from the sensations of this world. Shall you carry yourself as an energy suck? A Negative Nancy? Debbie Downer? Anhedonic Amy? Blue Bailey? Crestfallen Carrie? Exhausted Emily? Fallen Fanny? Grim Greta? Hung Hailey? Indifferent Isabelle? Jaundiced Janice? Killbuzz Katie? Low Laura? Morose ManMeat? Off Ophelia? Pessmistic Paula? Quiet Quinn? R'lyeh Riley? Sullen Susan? Torn Tammy? Underachiever Ursula? Villainous Vivian? Whining Wendy? Xhausted Xander? Yellow Yonnie? Zoophilic Zoey? No. I am *unsheathes sword* Holy Heart: Rider of the pink skies. Rolling and rumbling in all proportion to the wind, the uncontested legend of guava jam. HERE HE IS: In their 2022 incarnation, prepared to parade their plural sys–No, um. He is a man of many voices, however.

MANY.

       VOICES.

             AND.

                   YET,

                             ONE.

A

 


Okay, so to solve this, I'm takin' inspiration from the stocking stalky part of our Christmas episode, particularly the properties of closure.

Let's spose P Z. Then since Z is closed, there is a neighborhood V of P such that V ∩ Z = ∅, and thus

(i* )(V )	= (i-1(V ))
	= (∅)
	= 0

 
So given any element < W,s >∈ (i_* )_P,

< W,s >	=< W ∩ V,ρW,W∩V (s) >
	=< W ∩ V, 0 >
	= 0

 
So (i_* )_P = 0, as needed.

In the other case, P ∈ Z, I'LL WRITE IT IN STR8 ENGLISH:

1. This time, every neighborhood of P in X intersects Z
   
2. But that means these neighborhoods are exactly all the neighborhoods of P in Z
3. And since i_* inherits the restriction maps from ,
4. it's clear that (i_* )_P = _P

 
Done.

B

 

What is a man, but a can of spam? Dancing a cancan and jigging a guavic jam pilloried in the pink skies of fate. Repeating his favorite phrases under manyacontext, waiting for something, anything that comes out of his mouth to move, or hit someone, anyone. He'll spend hours at a mirror in his room, crafting with such care the most deliberate phrases and tones of voice, only to meekly and casually deploy them as offhand remarks and go ignored. All a man wants is attention. An ounce of recognition. And yet he will likely go his whole life, wrested all manners of expression from his voice, for all practical purposes unheard. His tsunami of words unleashed over the course of his life shall have touched no one. He begins to think not that his feeling are unexpressed by his words, but that his words are not English–or perhaps that he is the only one speaking English. He is speaking some sort of private language that gets machinetranslated into something mellow before it comes out of his mouth. That vacant smile from his interlocutor says it all. It's an expression of unimpression. Impress, to press upon someone–that's what he wants: The esoteric power to warp something in someone else's brain: Surely that's the prerequisite to not just love, but connection in even its more basic form? And hence, surrounded by people nevertheless, he feels alone. Alone. Alone. Alone. "This is going to be MY year," he said, for the 20th time. KNOCK KNOCK. Um, sir, you're about to default on your new year resolutions. "Shit, this is more of a pain in the ass than my student loans. Just kidding, nothing is more painful than that." It all comes down to spam. And thus: Spam is the highest form of humor. If your head and hands are aligned across 3 holes and you feel a sharp shadow looming over you, remember that you can start shouting "LOLOLOLOLOLOLOLOLOLOLOLOLOLOLOLOLOLOLO.." and everything will suddenly start to make sense... What?

And... uhhh... we're really calling this thing "j_!"...? Damn. Well, in that case, you know what I'm going to call the presheaf he gave us?

j?( )

=

 
So now I can say that j_! is the sheafification of j_?. HAHAHAHAHAHAHAHAHA. HOW DO YOU LIKE THAT? HOW CLEVER IS THAT? I am so proud of this notation. Somebody, please carry my throne to my dinner table. I must dine with pig and wine, for this day.

And now, we are going to be slick mathematicians and not do what Hartshorne tells us to do. Yes, we've seen Mr. Harty in the past try to rope us into doing extra work, but we're the goldhorned bulls of the herd. We grunt and puff air and jostle against command, laying our learned heavy eyes against gentle coaxing, and making our own slavery a struggle for our master. Rather than proving any properties from the construction of j_!( ), we'll uniquely construct j_!( ) from the properties: Killing two birds with one horn.

To be clear, the properties are that

1. That the stalk of the sheaf at P is
2. the restriction to U is

 
Got it? Now let's suppose is a sheaf on X satisfying (1) and (2). In particular, punching out property (2), let's suppose V ⊂ U is open. Then

|U	=
|U(V )	= (V )
i-1 (V )	= (V )
lim W⊃i(V ) (W)	= (V )
lim W⊃V (W)	= (V )
(V )	= (V )

 
(the last equality follows from the fact that V is an open subset of X). So for open subsets of U, we have a very convenient equality!!! And thus the equality also holds for stalks inside V . I'll write this as a lemma

0.1 Lemma

STMT

For V ⊂ U open, then (V ) = (V ).

QED

One more thing I want to establish before we get to the good stuff is what happens in the other case: P U. Well, immediately, _P = 0, and...

0.2 Lemma

STMT

If P U, then iven any neighborhood V of P and s ∈ (V ), ∃ a neighborhood W_P of P (note, W_P⊄U) such that ρ_V,WP(s) = 0

PROOF

Follows immediately from the fact _P = 0

QED

Okay, here's the good stuff. What do Lemma 0.1 and 0.2 tell us? Let's say W is open in X, and s ∈ (W) is a section. Let's check out all the stalks of s (CAN U GUESS WHY I'M DOING THIS READER???) If P ∈ U, then

sP	∈ P
	= P	(by Property 1 of )
	= (j?( ))P	(Lemma 0.2 yields WP⊄U that zeros out the stalk)

 
And if P U, then

sP	∈ P
	= 0	(Property 1 agen)
	= (j?( ))P

 
SEE WHAT I DID THAR? Check out the definition of sheafification again:



That's right, I just showed that for any section s of , that s_P ∈ (j_?( ))_P. I.e. The sections take the form of elements in the sheafification of j_?( ), satisfying the first property. Now, all I have to do is that s satisfies the second property, and I'll have that is the sheafification j_!( ) of j_?( ), and I'm done.

Now given P ∈ X, in the case that P ∈ U, I've got

(W ∩ U)	= (W ∩ U)	(Lemma 0.1)

 
hence t = ρ_W,W∩U(s) is the desired element satisfying t_P = s_P in V = W ∩ U.

Otherwise, in the case P U, then I know in the W_P set from Lemma 0.2, s = 0 (t = 0 in V = W_P is the desired element). DONE.

C

 


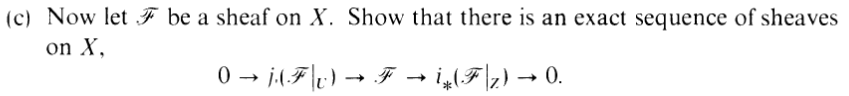
This is a VERY VERY SCARY exercise.... IF YOU ARE AN IDIOT.

Before I explain, let's actually work out what these maps are. We're making an exact sequence,

(1)

 
Let's start with

0.3 Defining ϕ

ϕ : j! |U

→

 
To define, ϕ, we need to define, given V open in X,

ϕ(V ) : j! |U(V )

→ (V )

 
Now recall (lemma 0.1) that if V ⊂ U, then

j! |U(V )

= (V )

 
So then we can just make ϕ(V ) be the identity.

And in the case V ⊄U, then the KEY POINT is that j_{! |U}(V ) ⊂ (V ) (EXERCISE LEFT 2 READER) so the ϕ(V ) can just be the inclusion.

So that's ϕ defined, and with injectivity working the way you expect you can immediately see that it's injective (AS WE SHALL SEE, I need not even point this out. We'll get it "automatically" later)

0.4 Defining ψ

 
We need to define

ψ(V ) : (V )	→ i* |Z(V )
i.e.ψ(V ) : (V )	→ |Z(i-1(V ))
i.e.ψ(V ) : (V )	→ |Z(V ∩ Z)

 
Now, in the case that V ∩ Z = ∅, then we get

ψ(V ) : (V )

→ 0

 
which is the zero-map

|Z(V ∩ Z)	= i-1 (V ∩ Z)
	= lim W⊃V ∩Z (W)

 
Since V ⊃ V ∩Z, the natural map in this case is s < V,s >. Alrighty, and so far we are going to AVOID talking about surjectivity and stuff as it's messy

0.5 The trick

As I said, this exercise is scary IF YOU'RE NOT CAREFUL. I saved myself from going down the rabbit hole on idiocy this time, out of sheer fear. Y'see, what's scary about exact sequences of sheaves is, as we learned back in 1.2 that surjectivity and images work so unintuitively. But what we ALSO learned is that we can get around that issue by going down to stalks, where surjectivity and image work as expected. So for every P ∈ X, as long as we show that the sequence of GROUPS

(2)

 
is exact, we're DONE!!! actually, A and B were buttering us up exactly for this. A tells us that...

(i* |Z)P

=

 
(last equality is a property of restrictions)
Similarly, part B tells us that

(j! |U)P

=

 
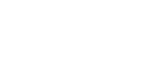NOW RECALL: in this part of the exercise U and Z are complements in X. WHICH MEANs (here's where things get slick as FUCK), when P ∈ Z, the sequence (4) turns into...

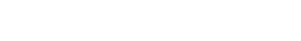(3)

 
and ψ_P is just the identity (following from the definition of ψ). So this sequence is clearly exact. In the OTHER CASE, when P ∈ U, the sequence becomes

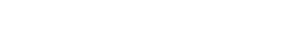(4)

 
and ϕ_P is the identity (following from the definition of ϕ). Clearly exact.

So (4) is exact for all P ∈ X, and hence (1) is exact by 1.2. DONE.

Wait a second... It's 1/5...? Seriously? You're telling me that I've already lost FIVE DAYS FROM THE NEW YEAR? Bro, it felt like two days ago I posted my NYE post, and it's actually been FIVE DAYS? I'M ALREADY DOWN TO JUST 360 DAYS LEFT?????? HOW DOES TIME FLY SO FAST. I got nothing done in these first 5 days LOL. You're already ahead of me reader... [Update: it's 1/6 now... it jut keeps getting worse...]