So I just saw the new Spiderman movie. The nonspoiler version is: It was FUCKING AWESOME. I loved how they brought back the old cast in a way that wasn't too on the nose. And yes, this is an absolute must-see in theaters. The audience's reactions for some of the reveals were honestly something that I won't forget any time soon. So yeah, highly recommended. I'm going to get into spoilers now, so if you haven't watched it definitely do so before reading this post.



Alright, spoiler time. Okay: I'm usually not one for nostalgia bait, but I'll admit when Andrew Garfield came on screen and the audience fucking screamed, I was grinning like an idiot. Collectively realizing we were getting a full-on multiverse movie was just a magical moment. And the fucking Tobey Maguire entrance? I kid you not: People were fucking jumping out of their seats when he appeared. I can't believe they pulled it off. What a fucking time. It was just a constant hype train from there. Seeing all the old villains gang up was also just pure bliss. Willem Dafoe was just excellent. Holy shit, what a ride. I wish I could go back and see it for the first time again. One of the best theatergoing experiences of my life, by far. Though what was up with that 10 minute rant in the middle by Tobey about how "Harvey Weinstein was innocent"? That was seriously inappropriate. How did that even get past the Hollywood censors? It's categorical misinformation. Everyone knows Harvey Weinstein is guilty. He was convicted by a jury in a fair trial, after all. But Tobey just kept going on making these false claims about how "He was set up" and "There was no actual evidence" and how "He literally did nothing wrong." It didn't even have anything to do with the plot. I remember Tom and Andrew tried to calm him down but Tobey just replied "My twink ass has been in Hollywood longer than yours," and the audience clapped for some reason. That line makes no sense in the context of the movie's universe. It was clearly just Tobey adlibbing or something. I know he got a big check, but were they that desperate to get him on screen? Seriously, I just don't think it's befitting of Peter Parker to tout conspiracy theories about how "Big Bad Harv" was "unfairly persecuted by the media" for "consensually tearing up goypussy." Putting these sorts of lies on the big screen is at best irresponsible and at worst dangerous. To his credit, Tom tried to play along and said "I see where you're coming from. That J. Jonah Jameson guy really gets on my nerves," but Tobey just smirked and said "Kid, when you grow up, you'll realize he's based" then started ranting about some journalist that wouldn't call him "Tugboat Maguire." At that point Zendaya finally had enough and called Tobey's comments "disgusting," but Tobey just replied "Hey lady, how bout you get me some milk and cookies?" and the audience clapped again. Extremely misogynistic. Did Sam Raimi write this scene or something?

A

 


Today's exercise is very cursed. Well, okay, Part B and C are, but part A is alright. What we're doing, in a broad sense here in 1.2, is relating sheaves to stalks. oh, and here's your sheaf kernel bro:



So the sheaf kernel is just the presheaf kernel, which has a "natural" definition. Cool. That makes part A not too bad. What I'm gonna do is take the map

δ : (ker ϕ)P	→ ker(ϕP)
[U,s]	< U,s >

and show that it's an isomorphism.

(Note my use of the different brackets to differentiate. I will do this in the later parts).

0.1 Cute and valid?

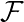Well, is this even a valid map? First of all: Is "< U,s >" even an element of ker(ϕ_P)? Well, since [U,s] ∈ (ker ϕ)_P, I know that s ∈ ker ϕ(U) ⊂ (U), so < U,s > is actually a valid member of _P. YOU ARE VALID, < U,s >. And furthermore it is in fact trivially a member of the subset ker(ϕ_P) ⊂ _P.

Okay, there's another thing we have to check since we're working with equivalence classes: Well-definededness Let's say that [U,s] = [V,t] Then we have a neighborhood W of P such that s_|W = t_|W on ker ϕ(W) ⊂ 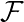(W), hence < U,s >=< V,t > in 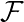_P, which ker(ϕ_P) is a subset of.

0.2 Surjectivity

Suppose < U,s >∈ ker(ϕ_P) ⊂ 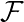_P. So s ∈ (U), and

0	= ϕP(< U,s >)
	=< U,ϕ(U)(s) >

So BASICALLY, I can assume that ϕ(U)(s) is 0 when restricted to some open set V . I.e. denoting the restriction maps as ρ, I know

0	= ρU,V (ϕ(U)(s))
	= ϕ(V )(ρU,V (s))

by commutative property of morphisms. HENCE, ρ_U,V (s) ∈ ker ϕ(V ), and thus [V,ρ_U,V (s)] ∈ (ker ϕ)_P, so..

[V,ρU,V (s)]	< V,ρU,V (s) >
	=< U,s >

0.3 Injectivity

ok this one is easier lol

δ([U,s])	= δ([V,t])
⇔ < U,s >	=< V,t >
⇔∃W : s|W	= t|W in (W)

Since ker ϕ inherits the restriction maps of , the last equality also holds in ker ϕ(W). Hence [U,s] = [V,t] in (ker ϕ)_P. DONE.

"Umm, what about the im part"... Ummm, I'm too lazy. I bet it's analogous anyway lolololol.

B

 


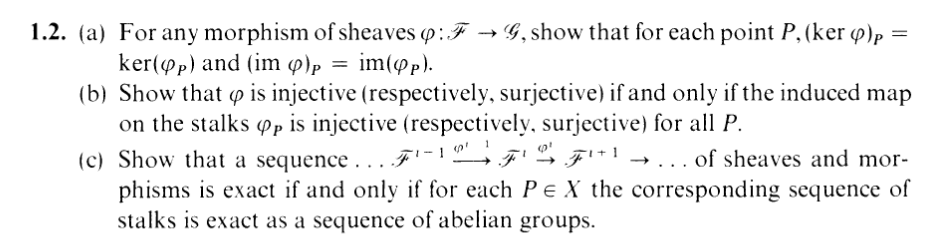
I almost vomited when I saw this part. There's already a proof in the book that proves almost the same thing but not quite. In fact, the closer you look, the more you realize this is QUITE a different beast. Y'see, before you get ahead of yourself and start working with the sectional maps, you have to ask: How are injectivity and surjectivity even defined for sheaf morphisms? Here's injectivity:



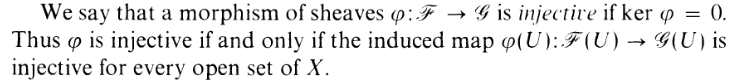
Okay, common sense! Works the way you expect. What about surjectivity?



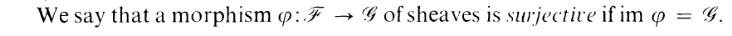
Now, I've heard certain dweebs complain about things like how the "quotient rule" is unintuitive and such. Hahahahahaha, cute. Let's just say they haven't seen true horror.



AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

WHYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY

So yea basically at this point, I just said "fuck it, I'm skipping this" and went on to the next part... Turns out... That was (unintentionally) a 999 IQ play. Watch this:

C

   


BTW: In case you're wondering, I didn't actually watch the new Spoderman movie lol. Spider-Man 2 (2004) is probably one of my favorite movies though. (And... fuck. can I just say Tobey Maguire is cute. "Ummm, you know he's a complete asshole in real life?" THAT. JUST. MAKES. IT. BETTER??? THE CONTRAST BETWEEN HIS BOYISH FACE/VOICE AND HIS FUCJING DOUCHEBAG PERSONALITY YES YES YES YES PLEASE). But yeah that aside I just can't get excited over this sort of stuff enough to buy tickets or even pirate it and watch it. I legitimately mean it when I say there is something admirable in the way people can get excited over the newest superhero movie or AAA game or anime or whatever, because over the past few years I've basically lost so much interest in media in general. I just no longer feel the joy of consooming. I don't just mean pop media either. A while back I tried playing a new VN by one of my favorite writers and I just dropped it in the middle even though I love his writing. I've just lost interest in everything. And it's not like I "dislike" myself for being like this (I have other reasons to dislike myself, lmao)–I kind of know why I'm like this now and why it has to be that way–but seeing everyone excited over things makes me feel kinda lonely.

"Ummm is this your 999 IQ play?" No, my 999 IQ play is this:



MUAHAHAHAHAHA, DON'T YOU SEE READER? IF I DO PART C, IT AUTOMATICALLY PROVES PART B............ WHICH MEANS HARTSHORNE WAS TRYING TO MAKE ME DO EXTRA WORK. WHAT THE FUCK.

Okie dokie, Let me first expand that and give you a whole bunch of new definitions:



Okay, so like injectivity, the kernel works the way you expect. However, the image–since it relates to surjectivity–doesn't. Right: Note that the SHEAF IMAGE is NOT U im(ϕ(U)). That is the PRESHEAF IMAGE. The sheaf image is the SHEAFIFICATION OF THE PRESHEAF IMAGE.

You know what that means, motherfuckers? YOU WANNA SEE TRUE HORROR, MOTHERFUCKERS? GUESS WHAT. IN GENERAL,

(imϕ)(U)

≠im(ϕ(U))

(1)

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

FUCKING WHYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY

Yeah, so if I denote the presheaf image as imp, then the right hand side of the above inequality is (impϕ)(U). It's slightly better than a straight up inequality though, as the RHS is a (possibly proper) subset of the LHS.

Okay, let's do this. We're comparing sequences

(2)

(3)

(P ∈ X) Let's start with the only-if:

0.4

Let's suppose (2) is exact, so

ker ϕi

= imϕi-1

(4)

We want to show that (3) is exact for arbitrary P ∈ X, i.e. we want to prove the equality

ker(ϕPi)

im(ϕ Pi-1)

BTW, note the parentheses. Alright. So let's take an element < U,f >∈ ker(ϕ_Pⁱ), so that

f	∈ (ker ϕi)(U)
f	∈ (imϕi-1)(U)	(4)

which does NOT necessarilly mean f ∈ im(ϕ^i-1(U)) thanks to the inequality of doom (1). But imϕ^i-1 is the sheafification of impϕ^i-1, whose sections are indeed im(ϕ^i-1(V )). So by the sheafification construction, I can claim that ∃ a neighborhood V ⊂ U of P, and a t ∈ im(ϕ^i-1(V )), such that t = f_|V . Hence < U,f >=< V,t >∈ im(ϕ_P^i-1).

Hence ker(ϕ_Pⁱ) ⊂ im(ϕ_P^i-1)

What a fucking mess. The other inclusion is a bit better. Given < U,f >∈ im(ϕ_P^i-1), again, I can get a section t such that < V,t >=< U,f > and

t	∈ im(ϕi-1(V ))
	⊂ (imϕi-1)(V )
	= (ker ϕi)(V )	(4)

so < V,t >∈ ker ϕ_Pⁱ. Whew.

0.5 ⇐=

ALRIGHT. LAST STRETCH. So now I'm supposing that (3) is exact ∀P ∈ X and I want to show (2) is. I.e. I know

ker(ϕPi)

= im(ϕ Pi-1)

for all P ∈ X, and I want to show

ker ϕi

imϕi-1

(5)

So given f ∈ ker ϕⁱ(U), I know that

< U,f >	∈ ker(ϕPi)
	= im(ϕPi-1)

which means ∃ < V _P,g_P >∈ 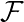_P^i-1 (g_P here is the section, not the stalk element) such that

ϕPi-1(< V P,gP >)	=< U,f >
< V P,ϕPi-1(V P)(gP) >	=< U,f >

Now I'm gonna denote h_P = ϕ_P^i-1(V _P)(g_P). Refining if necessary, we can assume that f|V _P = h_P. And since

hP	∈ im(ϕi-1(V P))
	⊂ (imϕi-1)(V P)

we can glue the h_P's together to form an element h ∈ (imϕ^i-1)(U). But by uniqueness, we must have h = f! Hence, ker ϕⁱ(U) ⊂ imϕ^i-1(U)

LMFAO. As I type this I realize I haven't done the reverse inclusion yet. I felt so exhausted that I felt I was done already. FUUUUUUUUUUUUUUUUUUUCK I'M SO FUCKING TIRED FUCK FUCK FUCK FUCK FUCCKKKKKKKKKKKKKKKKKKKKKK. OK, QUICKLY: Suppose f ∈ (imϕ^i-1)(U). Then for each P ∈ U,∃V _P,g_P such that f|V _P = g_P, and

gP	∈ im(ϕi-1(U))
< V P,gP >	∈ im(ϕPi-1)
	= ker(ϕPi-1)

AND THEN REFINE EM, GLUE EM, AND YOU'RE DONE! SEEYA IN THE NEXT EXERCISE READER.