II.1.17
12/24/2021
From the 24th of December at 9PM, to the 25th of December
at 3AM, are the 6 hours in the year that people are having sex the most–"The 6
Hours of Sensuality", in which Let us give up on it all. And then, let us fight.

IT'S CHRISTMAS EVE BITCHES. YOU KNOW WHAT THAT MEANS.
HYPE HYPE HYPE HYPE HYPE HYPE HYPE HYPE. AWWWW YEA
MOTHERFUCKERS, YOU KNOW IT. IT'S YOUR FAVORITE. IT'S TIME FOR
ANOTHER YEAR OF 性の6時間.
Hahahaha. It's funny because you're alone. HAHAHAHAHA LOOK AT
YOU, READER. EVERYONE'S HAVING SEX EXCEPT YOU. YOU'RE
READING THIS BLOG INSTEAD OF PARTICIPATING IN THE WORLD'S
GREATEST ANNUAL ORGYYYYYYYYYYY wait actually that's the
Great Barrier Reef party.
"Umm, that's great and all but why did you skip to 1.17?????" Well, I've said
before that I shouldn't overdo the amount of exercises per section I do. And this
section has... 22 exercises. Oh no! But when I
looked closer it turns out that the first half of them are just defining and
establishing basic objects in the category of sheaves, like direct sums
and stuff. Okay, that's great and all but this is less important than...
you know... actually fucking doing things with sheaves, which the
second half is about. I can deal with those constructions as they cum.

HO HO HO HO HO HO HO HO HO HO HO HO HO HO HO. ARE YOU
LONELY READER? WELL HOLEINMYHEART IS COMING TO TOWN. TO
FUCK YOU. I'M COMING TO YOUR
HOUSE TO FUCK YOU IN THE ASSHOLE.
I'M GONNA KISS YOU AND STROKE YOUR HAIR AND LICK YOUR NIPPLES AND YOUR TOES AND YOUR
GENITALS YES I'M GONNA SUCTION SUCK YOUR COCK AND STICK IT
IN MY EYE ("Dude, why do you keep making jokes about eye socket sex on your
website? It was mildly funny the first time but it's starting to get genuinely
creepy. It's almost like you have some kind of obsession about it and you
can't help but repeatedly bring it up as a 'joke' as a way of") WE'RE
GOING TO HAVE A LOT OF ANAL SEX. *pulls
your pajamas off and sticks my cock into your butthole
and starts thrusting extremely rapidly smiling while you moan in both
pain and pleasure tears fall out of your eyes in both sentimentality and
sensuality while in the background plays your favorite xmas song* *After
I cum inside you I wipe your butt with a tissue and kiss you on the lips
and complimenting you and whispering i love you into your
ear and kiss you on the cheek and i wipe my forehead in exhaustion*
Whew its been a long time since I've sexually assaulted the reader.
The first part of this exercise, btw, is pretty trivial. I'm gonna denote Z = {P}-
for simplicity. If Q ∈ Z, then by the definition of closure, for every neighborhood
V of Q, P ∈ V , which means the sections of each neighborhood of Q is A. So
the stalk of Q is A. If Q
 Z, it's the opposite situation. See? Ok? EZ. Bit too
Englishy but blejbljba.
Z, it's the opposite situation. See? Ok? EZ. Bit too
Englishy but blejbljba.
Uhhhh he more complex part is the second part about the constant sheaf. First of
all, here's the definition of the direct image:

Now I'm gonna go ahead and denote the constant sheaf here as
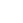 since that's less
confusing. So our map is i : Z → X and we're lookin' at the sheaf i*
since that's less
confusing. So our map is i : Z → X and we're lookin' at the sheaf i*
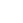 .
ALRIGHTY. So given open U ⊂ X, we have
.
ALRIGHTY. So given open U ⊂ X, we have
i*
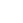 (U) (U) | =
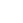 (i-1(U)) (i-1(U)) | ||
=
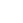 (U ∩ Z) (U ∩ Z) |
okay. SO if U ∩ Z = ∅, then P
 U, and also
U, and also
i*
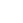 (U) (U) | = i*
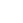 (∅) (∅) | |||||
| = 0 | (a basic property of presheaves) |
otherwise, U ∩Z≠∅, which means ∃Q ∈ Z such that Q ∈ U. But Z is the
closure of P, and U is a neighborhood of Q which means that Q has to
also contain P. So this is the P ∈ U case, and we know we have to get
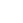 (U ∩ Z) = A. DO WE? Well, note that if we prove that U ∩ Z is
connected, we're done. OK. So since the singleton {P} is connected, so is
its closure Z, and so is the set U ∩ Z "in between" them (SAUCE)
(U ∩ Z) = A. DO WE? Well, note that if we prove that U ∩ Z is
connected, we're done. OK. So since the singleton {P} is connected, so is
its closure Z, and so is the set U ∩ Z "in between" them (SAUCE)
AND THAT'S TODAY'S. I'll make another post on NYE. MERRY CHRISTMAS.