With a stunning dearth of anything resembling intuition regarding the notion of ”separation,” let’s meditate a bit... Drops of dew on our fingers. Lick em. Young man, I do not mean to clear your mind, but to fill ’er up. You, me, we aint engineers of ye olde, trained neither theoretically to a T, nor in practice to a P. Is there a bigger picture to all this? This week, you are merely in love with the construction of this battery. A construction in a more ambitious location than your peers who broke the virginity: From here, you can show off your gallantry. We pick out locations that look like death zones, but are actually relatively safe, so long as you do well under stress. You do well under stress boy? You like the sound of fire? You link the beat of the bang? Look visible, it’s all for show: Give em something to engage with, but not hit. That’s the rule of coastal artillery: Buy high, sell low–I mean, build high, shoot low. Be a temptation–the fleur of their eyes. The more roundshot you swallow, the more you lure them in. Being under fire means they’re in range. Being under fire means they’re under fire. If you’re under fire and still standing, it means they’re stuck at arms-length–the sweet spot for red hot shot. Look at me. I’m not hiding behind the rampart, I’m standing on it. Is there something special about me? That I’m a short? A little thin, yet thick-skinned? I’m in plain sight, and I’m not dodging–they’re just missing. You see? My figure serves the purpose to confirm that measurement: That’s the location I picked out for you. And for them: My figure serves the purpose of imprinting my serious, young face into their minds. The face that cannot be hit, not because it’s special, but because it was intentionally placed there. And for you: Think of me as a scarecrow. A temporary decoration to your construction. I am to you as this carnation on my lapel is to me. Weak stemmed, onioning at the bloom. Your uniforms are no longer adorned with the feminine perfection of de-lis, and neither is mine with speculative euphoria of tulips (BUY HIGH, SELL LOW). My hands are dirty; I’m down to earthwork. A carnation: A bullseye that is actually a vortex. Every shot of theirs should peel back a layer, only to reveal more, while your brilliant red continues to seduce them: Into spilling their own blood. And when I alight from the rampart to construct another, who will take my place? Who would like to act as the measuring stick for who has who by the balls?

4.2

 

0.1 The set maps

We’ll begin by establishing that the set maps of f and g are the same. So in this subsection, we’ll only consider things in the set level.

Let’s start by looking into ”separation” a bit. The main diagram of reference, of course, is this one:



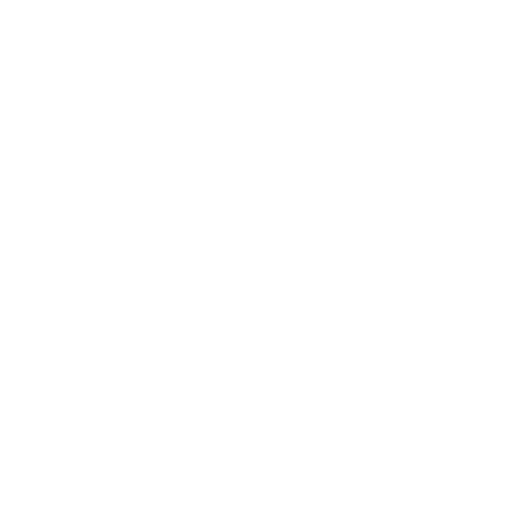
Note the identities i. I would like to break this up a bit. Let’s set Z = Δ(Y ). Then the fact that those i’s are identities, means that I can draw



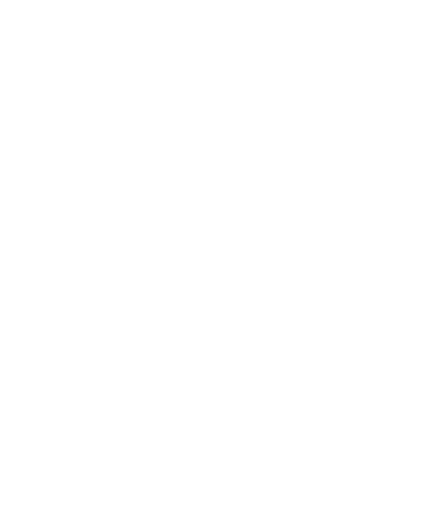
Now, surprisingly, I haven’t said anything about separatedness yet. All that is just how the diagonal works. All separatedness gives us is the fact that Z is closed. Hmm...

Now here’s something important (again, thanks to the identities): on Z, p₁ = p₂. If z ∈ Z, let y = Δ⁻¹(z) then

p1(z)	= p1(Δ(y))
	= i(y)
	= y
	= i(y)
	= p2(Δ(y))
	= p2(z)

 


Now, let’s bring X into the picture. To say that f,g are ”S-morphisms”, is to say that the following diagram commutes:



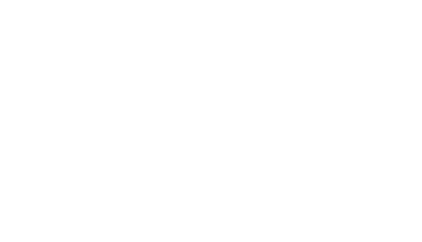
Where ∙ can refer to either f and g. Although we’ve guaranteed nothing about f and g being identical, when composed with Y → S, they terminate in the same manner. Which means that the following diagram commutes:

And I earn that dashed line, h, via the universal property of the fiber product.

Now what? Well, let’s imagine that we could replace the Y ×_SY with Z. Then I’d be able to draw this:



In particular,

f(x)	= p1(h(x))
	= p2(h(x))
	= g(x)

 

So we’d have f = g (as set maps).


READY FOR SOME TARGET×PRACTICE? TO A T, TO A P? Can you fit h(X) inside Z ⊂ Y ×_SY ? Because if you can, we’re done.

Ahh, all this abstract talk, and it feels like we’ve done such a huge amount of work, but we’ve done nothing. We haven’t used any property provided to us: Density, reducedness, separatedness. Now, I have hindsight, so I’ll tell you this. Separatedness is meant to be a generalization of T₂-ity. These spaces have the property that a two maps into them that agree on an open dense subset agree everywhere. We are proving this holds on set maps. Ideally, we’d invoke density and separatedness. It’d make even more sense to invoke separatedness, given that we’re already working with the diagonal. And it’d make sense to invoke density because it would be frightening if we proved the equality of two set maps without doing so.


Target practice? Let’s refine this even more: Let’s refine the tip of our arrow. Would it not suffice to merely fit h(U) into Z? Because in that case,

Z	⊃ h(U)
h−1(Z)	⊃ h−1(h(U))
	⊃ U	cheatsheet

 


Now HERE’S where separation would come in: Z is closed, so h⁻¹(Z) is closed. h⁻¹(Z) is a closed set containing the open dense subset U. Hence h⁻¹(Z) = X. This argument is inspired by an old one back in varietyland, from Hartshorne himself:



So

h(X)	= h(h−1(Z))
	⊂ Z	cheatsheet

 


AND WE’RE DONE... Or we would be done, provided that we prove the following inclusion

 


Now, certainly it must have something to do with the fact that f and g are equal on U. Here is my argument. Define:

(1)

 

which is the same whether I use f or g for X → Y . That gives me this guy:



However, you can check that the following, more complicated diagram also commutes:



Now d (1), the way we defined it, is made up of f and g, so letting h′ be the restriction of h to U, I can even draw:



But the map obtained by universal property of the fiber product is unique, hence
 

h′	= Δ ∘ d
h′(U)	= Δ(d(U))
h(U)	= Δ(d(U))
	⊂ Δ(Y )
	= Z

 


And we are done.

0.2 The sheaf maps

Now we have to show that the sheaf maps are equal, and it suffices to do this locally. So let

 


be maps of affine schemes that agree as set maps, and agree fully on an open dense subset U. Assume X is reduced. I need to show that the corresponding maps

 


are equal. I.e. given b ∈ B, I would like to show that f ∗ (b) = g ∗ (b). Now, let D(h) ⊂ U (assume h≠0). Then the restrictions

 


are equal. And thus so are the corresponding ring maps

 


But these maps can be factored as

f′′ : B	A → Ah
g′′ : B	A → Ah

 


Hence,

f′′(b)	= g′′(b)
∃n ≥ 0 : hn(f ∗ (b) − g ∗ (b))	= 0

 


Let x = f ∗ (b),y = g ∗ (b). I want to show x = y. Again, what I do have is

(2)

 


(Remember, we might not be an integral domain, so no zero-product-property here). This is far as a I got without looking at the solution (+1). The most blatant issue was not being aware of the construction that is the annihiliator:

 


In particular, this is an ideal.

What’s worse, however, is that there is another crucial assumption that the solution makes:

Where that comes from is a complete mystery to me. But I gotta move, and I am not delaying this post another week to figure it out.

Now that we have introduced the annihilator, it’s time for a lemma:

0.2.1 Lemma

For any n > 0, D(h) ⊂ V (Ann(hⁿ))

Proof

Let P ∈ D(h), so h P. Now let s ∈ Ann(hⁿ). Then hⁿ ⋅ s = 0. Since P is prime, hⁿ ∈ P or s ∈ P. But hⁿ ∈ P h ∈ P, a contradiction, so we must have s ∈ P. Since s was arbitrary, Ann(hⁿ) ⊂ P i.e. P ∈ V (Ann(hⁿ)).

QED

Suppose n > 0. Then we can apply the lemma: Let α = Ann(hⁿ), so D(h) ⊂ V (α). Since D(h) is dense, V (α) = X. This is again inspired by Remark I.3.1.1



So α = (1), which means that 1 ∈ Ann(hⁿ). Hence

hn ⋅ 1	= 0
hn	= 0

 


But we assumed n > 0, making h nilpotent. But X is reduced (THERE SHE IS), so that would mean h = 0, a contradiction. Hence n = 0, and (2) becomes

h0(x − y)	= 0
1 ⋅ (x − y)	= 0
x − y	= 0
x	= y

 


Done.