Imagine ruining your own reputation and legacy over a misguided ”cause.” Believing in something so wholeheartedly that you put everything on the line for it, only for it to end up in the gallows. Imagine the delusion it must take to dedicate oneself to a cause, without promise nor likelihood of its success, just because you think it’s ”right.” Regretting it when your great fantasy of being on the front lines of a colorful counterrevolution comes crashing down, and the realization finally sets in that your entire ”movement” will be crushed so easily it’ll barely make the daily news. Imagine having a sword stuck into your chest, breathing your last breaths, and realizing that what you ”stand for” will be suppressed and never echoed again. That in the end, no one cares about your convictions. That people only care about your results, and everyone–good and bad–will mock you for your lack of shrewdness in taking up your cause. Imagine ”believing” in something, as if life should be subservient to the whim of belief. As if that's all life is: A walk to an abstract end, rather than the moment-to-moment color in the means. Something to strive for rather than live for. Imagine snuffing out your imagination with someone else’s ideology. Indeed: Imagine hooking your entire life onto an idea, just because you think it’s ”right,” as if ”right” is more important than ”significant.” Believe in one ”system” over the other? As if a system is defined by its theory rather than its practice–how well its human actors wield personal and cultural influence in the moment. Imagine manhandling her tiny body, just walking around the house looking for things to bend her over and fuck her on. Imagine grabbing her by the ankles and holding her up like a chicken carcass, swinging her around as she whines. Imagine that frightened look on her face when it’s time to take out your frustrations again on her stupid little body. Imagine her gleaming, bruised smile under your warm embrace.



A ONCE GREAT CITY, now drenched in the color of love, with all in motion in indefinite arrest, in the warm embrace of uninsurrection. The remaining air still, unmovin an unmoved, in wait of its next nother taking: A transitory period–the trance of rehabilitation–begins. A new day awaits decades ahead, while it asides to something greater somewhere souther. It lives on, nominally mock-dead, and physically in mock-continuity. Lays quiet, in gestures of regret. The scant federalism scanted. All that was boasted, inverted, and their bodies turned inside out, and minds realigned. Red and gold turned red white and blue. You strangled the stragglers. Garotted the Girondins. Hung them by the balls on the cursive hooks which echo their royalism. Splayed em open and handled their pouring guts like an anaconda. You proceeded down the main aisles holding high piked heads bobbing in the rhythm of a Turkish march. Now: Resentment held in, and checked for the time being. Members going through our motions, and dismantling under our eyes their own ideas. A once great city, reduced to a hub of resources. Imagine having built years into your trade, raising a promising populace, accumulating a reputation, and losing it all for a ”noble cause” that goes absolutely nowhere. Imagine finding out that you are merely a prelude to the stage set further south: A siege set in bluegray. A fugue with young subjects in revolution, counterrevolution, and counterpoint.



I need some ammo, Rep. Ammo, ammo, ammo. You sure you can’t pull a little from the Army of A, a little from the Army of B? THEN, I propose we export that flavor of extortion I just described to the villages dotting the area here. To all these retired royal men, fencesitting in old chairs, impassionate to the touch of the young, but fearful of your wrath. Go to them, take me with you, and I’ll imprint your ugly face into their heads. Do I sound bloodthirsty? Well, I don’t like being like this, but the lack of ammo is really screwing with me. As you can see, I’m in quite a pinch. An ammo pinch. Ammo ammo ammo ammo ammo. Boy oh boy, if you couldn’t tell, I really want some ammo right now. I’m mostly exaggerating. Just kidding, I’m not. I’m dead serious. I mean dead. I’ll make them hand it over by force, ysee. I’ll make them crawl to my park to repair those old iron suckers: Old suckers to repair old suckers. Where does the veteran’s alleigance lay? Try a bit of humiliation, eh. If his wife’s pregnant, playfully poke your bayonet at her stomach while chatting about the navy, and you’ll find out. Do I sound bloodthirsty? I’m not. I’m ammothirsty. I’m more hungry for ammo than anything else. More than victuals. More than the taste of a woman’s thigh. Can I please, please, please have some ammo? I’ve been using peat as gunpowder. Screw it. Expose the children. Kill the women. Kill the men. Kill em all. MASSACRE THEM. HANG THEM. PAINT THE CITY RED. Just get the ammo for me. That’s all anyone really needs, right? Ammo. If everyone had some ammo, no one would need to shoot. That’s how i feel. I really really really wish I could get some ammo right now. Ammo, ammo, ammo. God I am hungry for ammo. I’d strangle a child right now for some ammo. Spinny balls. Red hot shot. Appleshot. Grapeshot. Bananashot. Canisters. I have to wake up early tomorrow, and i’m always running on too little sleep. I’m in a constant manic panic going through the day. my mind is all over the place and hyperattentive. I’m just whoooooooooo. The least i could have is a little ammo. Ammo ammo ammo ammo ammo ammo ammo ammo ammo ammo. Ahhh, ammo. To sweeten the day. That’s all a parvenu needs. Ammo. Come onnnnn, gimme some. GIMME SOME, you Reptile. Gimme the ammo. GIVE ME THE AMMO, REPRESENTATIVE. COME ONNNNNNNNNNNNNNNNNNNN MR REP. USE YOUR NAME AND GIVE ME SOME AMMO. COME ONNN, REPPY, DO IT YOU FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF. GIVE ME THE AMMO REPERERERETEREERETERERTERERERRERERERERERE. COME ONNNNNN, YOU DUMBASS. JUST HOW DIFFICULT IS IT TO SIMPLY. OBTAIN. SOME. AMMO. MR REPRPEPRPERPERPERPERPRPEPRPERPER IS IT ALGEBRAIC GEOMETERY???? IS IT THE DIMENSIONS OF A CONICAL MORTAR HOLE? WHY DON’T I HAEVE AMMO YET REPRPEPRRRRRRRRRRRRRRRRRRRRRRRPEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEERRRRRRRRRRRRRRRRRRRRRRRRERPEEEEEEEEEEEEEEEEEEEEREEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEERRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRRREEEEEEEEEEEEEEE. Mr. REEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEP, YOU HAVE HTE POWER TO SLICE ANYONES HEAD OFF AND YOU CANT EXTORT ANY DAMN AMMO? TOO BUSY WATCHING MY GF GIVE YOU NUDE DANCES????????? LOL, MY BLUE BALLS RIGHT NOW CAN ONLY BE FULFILLED WITH SOME AMMO. AAAAAAAAAAAAAAAAHHHHHHHHHHHHH, Mr. RREPPPPPPPPPPPPPPPEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEREEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEESEEEEEEEEEEENTAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAATIVE I WANT SOME AMMO. PLEASE, PLEASE, PLEASe you FAGGOT LIZARD, WHY DONT WE HAVE ANY AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMMOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO I’LL KILL YOU I’LL KILL YOU, I’LL, KILL YOU. I’LL KILL YOU AND YOUR WAIFU. I'M THE WAIFU KILLER, REPRESENTATIVE. I’LL KILL YOU AND I’LL KILL YOUR WAIFUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUU MR. REEEEEEEEEEEEEEEEEEEEEEPEEEEEEEEEEEEEEREEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE





”we will use definitions that reflect the functorial behavior of the morphism within the category of schemes.” That’s right. If you are wondering why I have only a single exercise to present after a whole 2 weeks, it is because this is a new section, and its exposition was painfully abstract and difficult to get through. And, as you shall see, the fact that I made a major flub that got me stuck for days. And, no ammo.


Let’s get the preliminary definitions out of the way. A separated morphism has a closed diagonal:





A ”proper” morphism, on the other hand, is separated with some extra sugar:



That is all we need for today, but there are alternate criteria ”using valuation rings”, which is where this section truly gets ugly. For now, though, we won’t worry about that. I have to learn a lesson about ”alternate criteria” first.

4.1

 



Let f : X → Y be finite. Then it is trivially finite type, so we need to show that it’s universally closed and separated. Since finite morphisms are closed (which I haven’t proved) and stable under base extension (which I haven’t proved), it’s clearly universally closed.


Now I have to show that it’s separated. In other words, I need to show that the image of the diagonal is closed. Take a look at this diagram:



(The i’s mark identity morphisms). Thanks to stability under base extension, I know that the g’s are finite. So what about Δ? If it were finite, then we’d be done, since finite morphisms are closed.



Let’s do it in a lemma.

0.0.1 Lemma

Consider this diagram




where g is finite, and i = g ∘ f is the identity. Then f is finite.

Proof

And this is where I got helplessly stuck for days. Days, days, days...

Let’s look at my mistake, and perhaps you’ll find a moral to this story. Recall the definition of finiteness:



Now, do you remember how we had an alternate criterion for it (which I haven’t proved)?





WHICH HE HASN’T PROVED. 3 times in a single post. Listen: I am no math student. I’m not an adherent to ”If you use it, prove it.” That is for mathematicians. I am a commoner. I’m one of yall, which is why I can get tangled up in these vines. Should we use the original definition to prove this lemma, or the 3.4 criterion? Certainly, the criterion of 3.4 is fancier, and dealing with one open affine seems less busy that dealing with a whole cover of them. So why not use the 3.4 criterion?


Try proving this, reader: If V = SpecB ⊂ Y is an open affine in Y , show that U = f⁻¹(V ) is an open affine SpecA in X, with A a finitely generated B-module. Can you do it? Can you even show that f⁻¹(V ) is affine? Have fun.


I had fun for 5 days straight. I had fun desparately trying to find an open set of X inversely mapped onto V via g. I went in loop-de-loops of identity morphisms, composing f with g and vice-versa. I drew wacky commutative diagrams that all turned out to be redundant. Perhaps had I proved 3.4, I would have realized something. But I did prove an analogous equivalence in 3.3c, didn’t I? Do you see how much work that took? To get from ”initial definition” to ”stronger looking criterion”? Shouldn’t I have taken note of that, and gotten suspicious?


Thricegreat laughs from the shadows. Oh sure, both the initial definition and the 3.4 criterion nail down the concept that is a finite morphism equivalently. But equivalence isnt everything. Equivalent they are, yes, but we’re humans, not robots. To the human eye, the initial definition is ”weaker” than 3.4. And that’s what matters. Not logic, but feeling. Use the right tool for the right job: Weaker criteria are easier to prove, stronger criteria are easier to use. Here, I was trying to prove that a morphism was finite, not use a morphism that I already know is finite. Look at how simple this becomes when we just fall back to the initial definition.



Let

 

be an open affine cover of X, with U_i = SpecA_i. Then

Y	= g−1(X)
	= g−1(⋃ i∈IUi)
	= ⋃ i∈Ig−1(U i)

 


Now I know that each V _i = g⁻¹(U_i) is affine, SpecB_i, with B_i being a finitely generated A_i-module. I have an open affine cover of Y , and if I preimage it with f,

f−1(g−1(U i))	= (g ∘ f)−1(U i)
	= (i)−1(U i)
	= Ui	= SpecAi

 


There you go. By just swapping definitions, I got to a point I couldn’t get to for 5 days... in 5 minutes. All we have left to do is to show A_i is a finitely generated B_i-module. Yes, we have to prove that from the fact that B_i is a finitely generated A_i-module. A little weird, huh? But remember, we don’t mean any finitely generated modules, we mean the ones precisely induced by the morphisms of affine schemes

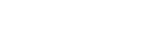(g ∘ f the identity). i.e. the corresponding ring morphisms,

 


Now, I know that f′∘ g′ is the identity, which means that I can actually draw this as

 


Point being, f′ is a surjection, making A_i a finitely generated B_i-module.

BONUS ROUND: 3.18

 

This is completely unrelated topological hogwash that I spent time on and may not even end up revisiting. But we might as well stick it into the ledger anyway.

A

 

To begin: I HAVE LEARNED MY LESSON ABOUT ALTERNATE CRITERIA. In that, I’m skipping this part. I would instead like to define a constructible subset as the finite union of disjoint locally closed subsets:

 


And I shall take Hartshorne’s 3 abstract properties as mere consequences of this definition. The framing of constructibility above will be how we treat it, because it is far more useful for us, in the scope of this exercise. Use the right tool for the right job.

B

 

0.0.2 Dense constructible

Letting ζ denote the generic point of X, let’s suppose S is any subset. Then

S	∋ ζ
S	⊃{ζ}−
	= X

 

S = X means that S is dense in X.

Now let’s suppose S is constructible and dense. Let

 


Now, since Zariski spaces are Noetherian, I can break up each C_i into its irreducible components:

 

Which means I can rewrite S as

S	= ⋃ i=1n(U i ∩ Ci)
	= ⋃ i=1n(U i ∩ (⋃ j=1riD i,j))
	= ⋃ i=1n ⋃ j=1riU i ∩ Di,j
	= ⋃ i,jUi ∩ Di,j

 

(i,j ranging finitely). Now, since each D is irreducible, the open subsets U ∩ D is dense. Hence each U ∩ D = D. So

S	= D1,1 ∪ ∪ Dn,rn
	= C1 ∪ ∪ Cn
X	= C1 ∪ ∪ Cn

 

So ζ ∈ C_i for some i. Hence ζ ∈ S. Done.

It contains an open

EXERCIEASE LEFT TO READEAR

C

 

Closed

Let’s suppose S ⊂ X is constructible and stable under specialization. We’d like to show that it’s closed (the converse is obvious, thanks to 3.17??, which as I noted applies to any space). As usual, set

 


Now note:

x	∈ S
{x}−	⊂ S
S	= ⋃ x∈S{x}−

 

The problem here is that we have a possibly infinite union of closed, which is not necessarily closed. This is where constructibility comes in. For each of those x ∈ S, we have x ∈ C_i for some i, and thus {x}− ⊂ C_i. So we can just write

 

Done.

Open

Suppose T ⊂ X is constructible and stable under generalization (again, converse is obvious).

 


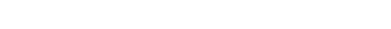You can guess how this ends, but we still have to get there.

Given x ∈ T, I’m going to intersect all open neighborhoods of x, setting

 

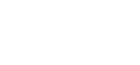If y ∈ U_x, then every neighborhood of x contains y. In other words, x ∈{y}−. In other ”words,” y ⇝ x. IN OTHER WORDS, y, generalizes x. Hence y ∈ T by stability. I just proved that y ∈ U_x y ∈ T. IN OTHERERERER WOROWROWRDS, U_x ⊂ T. And I can write

 

Now, our problem is that each U_x is an infinite intersection of open sets, which may not be open. But

Ux	⊂ T
Ux	⊂ U1 ∪ ∪ Un
⋃ x∈TUx	⊂ U1 ∪ ∪ Un
T	⊂ U1 ∪ ∪ Un

 

Done.