Ah, the sweet gray morning overlooking the southern coast. The stage is set for a standoff. Thar’s the silhouetted promontories of finiteness, their outlines vaguely waving like ghosts in the fog. What terrible manner of savage battery and slanted hand-to-hand combat awaits us on those rocks. And those natural titans spread, like a horseshoe around the Rade. Thar’s that famous crescent harbor, with a congregation of famous royalty entering so grand into the pool. The Aurore, San Juan Nepomuceno, and other ships of the line parked in the sea stadium, waiting for us little geometers to approach their magnificent algebra. There’s a dubious white chalk line, drawn by our commander marking the out-of-range zone, yet everyone’s found ominous roundshots sitting by the encampments. The algebra haunts the young boys’ nightmares. They feel molested, terrorized by its symbolic taunts. The frigates are obscured in awful majesty by the fog. Their cannons point at us even while we’re asleep. The commander can’t hide his pessimism. We’re not going to make it this time, are we. We outnumber them, but that doesn’t amount to much. We’re just newbies, man. We’re incompetent. These are academics we’re up against. They know what they’re doing. They’ve got control of the high ground and the seas, experienced professionals, and a whole host of expert force multipliers. We can’t win against that. How am we going to deal with relativity if we can’t grasp something as basic as tensor products? It just doesn’t click, or bang. The algebraic terrain ahead seems unbesiegeable. Things are moving slow on our end: It’s taking weeks to pick off pontoonal problems. And in the meantime, they’re fortifying the high ground and establishing supplylines on the seas. We’re supposed to besiege 23 exercises without any 24 pounders? Capture it in a month? What kind of siege is it when the besieged gets as much food as they want? Those folks are enrolled fulltime, living amongst each other in their academic frigates, poring over mathematical text day and night. Are you ready to see how far you can escalade up that rocky promontory, before dying by volley, all in the name of ”measuring their artillery”? Are you ready go set up a battery on that white line, and die in the name of ”quasi-finiteness”? Is the commander really giving us the full picture here? Is he leaving things out that would be filled in with lecture? He’s talking to university students. He’s talking to people pursuing degrees. But we’re not academics. We’re just ordinary boys. We’re gonna lose.

3.2

 


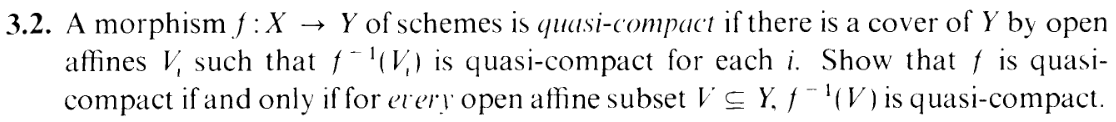
Easy, right? Yours Truly forgot that affine schemes are quasi-compact, and got stuck here for two days. Yes: Horrific start to the week, and thereby an awful effect on morale. [incidentally, the proof back there also traumatized Clam Hanson, as well as Zorn’s Lemma fanatics] At least from there, it’s trivial. Like last time, the ”if” is obvious, so we take on the ”only if.” We suppose that f is quasi-compact, so there is an open affine cover of Y :

 

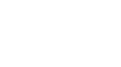where each f⁻¹(V _i) is quasi-compact. Now let V ⊂ Y be an arbitrary open affine. Then

 

is an open cover for V . And SINCE V IS AFFINE, IT’S QUASI-COMPACT, SO IT HAS A FINITE SUBCOVER:

 

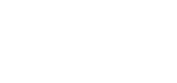So, in addition, note that

f−1(V )	= f−1(⋃ i=1nV ∩ V i)	(1)
	= ⋃ i=1nf−1(V ) ∩ f−1(V i)	(2)

 

Our goal is to show that f⁻¹(V ) is quasi-compact. Let’s suppose we’re given an open cover of it:

(3)

 

So, intersecting (7) and (5),

f−1(V )	= (⋃ j∈JUj) ∩ (⋃ i=1nf−1(V ) ∩ f−1(V i))
	= ⋃ i=1n ⋃ j∈JUj ∩ f−1(V ) ∩ f−1(V i)
	= ⋃ i=1n ⋃ j∈JUj ∩ f−1(V ) ∩ f−1(V i)
	= ⋃ i=1nf−1(V ) ∩⋃ j∈JUj ∩ f−1(V i)
	= ⋃ i=1nf−1(V ) ∩⋃ j=1miU j ∩ f−1(V i)	(since f−1(V i) quasi-compact)
	= ⋃ i=1nf−1(V ) ∩⋃ j=1mU j ∩ f−1(V i)	(m = max(m1,…,mn))
	= (⋃ j=1mU j) ∩ (⋃ i=1nf−1(V ) ∩ f−1(V i))	(wrapping back up)
	= (⋃ j=1mU j) ∩ f−1(V )	(yes, these comments are jutting out)
f−1(V )	= ⋃ j=1mU j

 

3.3

 


Here’s the definition of ”finite type” again. It’s locally finite type except the open covers of the inverse image are finite:


So, so, we continue on. There is a lot of mathematics for y’all this week, more than usual. We have to step it up for the road ahead. Yes, I took great pains to at least touch base with each of the first 7 exercises this week. In order to emphasize the odd fact that we seem to be studying morphisms rather than schemes themselves, and furthermore all under the umbrella of ”finiteness.” And also in order to get some kind of foundation set up quickly, as the road ahead gets real.

A

 

The ”only if” is obvious (thanks to 3.2). Now let’s suppose f : X → Y is finite type. Then it’s obviously locally finite type, so we need to show it’s quasi-compact. I’ll use the open cover definition of quasi-compactness. Since f is finite type, there is an open affine cover of Y :

 

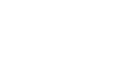where for each i, there is a finite open affine cover:

(4)

 

now let’s suppose we’re given an open cover

(5)

 

Then intersecting (7) and (5) and following an analagous argument to 3.2 gives us a finite subcover.

B

 

Trivial.

C

 

Steady boys. This is a long one, but we’ll take it.

First, let’s apply 3.3B, and obtain a finite open affine cover of f⁻¹(V ):

 

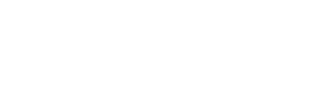where each A_j is a finitely generated B-algebra. Now, with U = SpecA ⊂ f⁻¹(V ), my goal is to show that A is also a finitely generated B-algebra. So let me cover it with the U_js:

U	= ⋃ j=1nU j ∩ U
	= ⋃ j=1nSpecA j ∩ SpecA

 

Okay, first note that each SpecA_j ∩ SpecA is an open set of SpecA_j, where A_j is a finitely generated B-algebra. I can apply last week’s lemma to obtain an open covering of SpecA_j ∩ SpecA made up of open basis elements W_ji of SpecA_j that are spectra of finitely generated B-algebras:

 

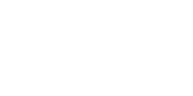But this constitutes an open cover of U, which is affine and therefore quasi-compact, so it has a finite subcover.

 

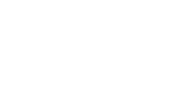I’ll simplify the union without loss of generality

 

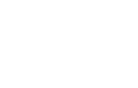The point is that each W_j, thanks to last week’s lemma, is the spectrum of a finitely generated B-algebra, as well as a basis element of SpecA_j. Now the problem here is that I’m trying to derive facts about SpecA, so I would rather have open basis elements of SpecA. So I am going to refine my cover in a way that I still get a finite cover of U by spectra of finitely generated B-algebras.

Okay, follow me along here:

1. I cover each of the W_j (which are, after all, open sets of SpecA with basis elements D(f) of SpecA, and applying the lemma again (yes, again) on each W_j, I can assume each D(f) is the spectrum of a finitely generated B-algebra
2. This cover has a finite subcover since W_j is affine and therefore quasi-compact

 
So now I get a new open cover of U:

 

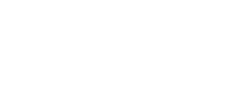where D(f_j) is an open basis element of SpecA (therefore f_j ∈ A. This is why I did that whole refining procedure) and each 𝒪(D_fj) = A_fj is a finitely generated B-algebra.


NO MORE GEOMETRY LEFT THIS EXERCISE. WE REDUCED THE PROBLEM TO PURE ALGEBRA.


Here is the new algebraic problem:

Let’s solve it. For each j = 1,…,n, I have a surjection

 

(Took m sufficiently large)

To rephrase: for each j, there are some d_j1,…,d_jm that ”polygenerate” A_fj (”Polygenerate” is a term I made up to say I’m using these folks to generate as a B-algebra as opposed to generating an ideal of A). The issue is that these polygenerators have denominators in the form f_j^r and polygenerate A_fj, whereas I want polygenerators in A and for A. I want to get rid of those denominators and still get all of A.

It pays to be greedy sometimes. What we’re going to do is simply multiply them out and see what happens. Watch:

Let’s say that a ∈ A. I want to polygenerate it with elements of A, but for now, let’s polygenerate it with elements in each A_fj. There are polynomials g₁,…,g_n ∈ B[x₁,…,x_m], such that

g1(d11,…,d1m)	= a
gn(dn1,…,dnm)	= a

 

I can also denote the left hand elements as β_i(g_i). Just remember they’re polynomials over the polygenerators, and the issue is the denominators. So now, taking N sufficiently large, I’m going to multiply out all the denominators

f1Nβ 1(g1)	= f1Na
fnNβ n(gn)	= fnNa

 

Looking a bit ugly, but if I add all those equations together. I can factor out the a:

f1Nβ 1(g1) + + fnNβ n(gn)	= f1Na + + f nNa	(6)
	= (f1N + + f nN)a	(7)

 

Now, the reason I did this is because, thanks to the exposition, I know that I can get rid of the f₁^N + + f_n^N. I’m going to go ahead and prove that result in the stronger form that I need.

0.0.1 Lemma

Suppose

(8)

 

Then, given N, the f_i^N also generate the unit ideal. In particular, we can make

 

where the h_i are each polynomials over the a_i and f_i

0.0.2 Proof

(a1f1 + + anfn)(n ⋅ N)	= 1(n ⋅ N)
(a1f1 + + anfn)(n ⋅ N)	= 1

 

Now apply the multinomial theorem for the left hand side:



Note that in that big sum in our case, thanks to the Pigeonhole principle, each term has at least one f_i with an exponent at least N. So 1 ∈ (f₁^N,…,f_n^N), and furthermore the coefficients of the f_i^Ns are composed of other f_is and a_is

0.0.3 QED

Okay, let’s finish it off. Now, via the lemma I can modify (7) to be

h1f1Nβ 1(g1) + + hnfnNβ n(gn)	= (h1f1N + + h nfnN)a
	= a

 

The left hand side is, in total, a polynomial over all the:

1. All the generators d_ji of each A_fj, with the denominators removed
2. f₁,…,f_n (to compensate for the removed denominators)
3. a₁,…,a_n (to get the f_is out of the way)

 
This choice of polygenerators doesn’t depend on a, so I just found a gigantic polygenerating set for A. Whew.

3.4

 


Instead of doing this exercise, we’ll use it as a rest stop. Here, you can play with the pidgies:

3.5

 


...

What are we supposed to do? We’re just... a ragtag group of juniors. The seniors are indecisive, too self-involved, resting inland on their laurels. And too archaic to efficiently teach us the basics. They skim over crucial technical details thinking that we’ll assume them naturally. What happens when the universities burn down and a new generation needs to carry the torch? Do you know how to fix a shot? I don’t. No one taught me. I dunno about you, but I don’t know anything. I don’t know what I’m doing. Everyone seems like they know what’s going on and acts like only a fool wouldn’t understand. But I don’t. I don’t. How do other people do it? How do they figure out what needs to be done and how? How do they get where they need to be? I wish I wasn’t the only one. I’m lonely. Lonely in all my stupid ignorance. Help. If it all collapses, I’ll be the first to go. If we get sent out there together, do you think we can make an alternative formulation that won’t end in vain? Do you think we can intuit what is really at play? Do you think we can draw lines in the sand and figure out something our commander may be leaving out? Or, at least, if we get sent out there, will you hold my hand?

A

 


Many novice geometers will die on this hill (or even the previous ones) if they naively follow Hartshorne’s instructions. Hartshorne can’t teach a layman to save our lives:




Is this correct? Let’s focus on the ”finite morphism” definition first. For simplicity, pick an i and denote V = V _i, B = B_i and A = A_i. Firstly, the novice geometer may wonder what in the world a ”finitely generated B-algebra which is a finitely generated B-module” even is. Here’s the thing: In schemeland, we are working with commutative rings, so for all intents and purposes here, a ”B-algebra” and a ”B-module” structure on A are, essentially, the same thing. They are just a ring morphism

 

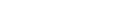The distinction comes only with the stipulation of being ”finitely-generated,” because in either case, ϕ extends in a different way. If it is a finitely generated algebra, it extends to a surjective ring morphism

 

But if it is a finitely generated module, it extends to a surjective module morphism:

 

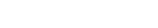What Hartshorne means here by ”finitely generated B-algebra which is a finitely generated B-module,” is essentially that the B-algebra and B-module structures on A must be induced from the same morphism, ϕ : B → A. The reason he doesn’t just say ”finitely generated B-module” is simply to ensure that ϕ is indeed a ring morphism, and not just a module morphism (i.e. that we get that extra property that distinguishes algebras from modules: preserving multiplication).

So Hartshorne stipulates that A must be ”a finitely generated B-algebra which is a finitely generated B-module.” Now here’s where the eagle-eyed novice geometer may notice something strange. ”a” finitely generated B-algebra? ”a” finitely generated B-module?



Which B-algebra/module structure is he talking about?



For example, given any ring (or, more generally, group) A, I know that the natural map

ϕ : Z	→ A
x	x

 

produces the well-known Z-module structure on A. But that isn’t the only one. E.g.:

ϕ2 : Z	→ A
x	2x

 

This is a different Z-module structure on A. x 3x induces yet another on, and so on. In general, there are many different B-module structures on A, so which one are we talking about? If you take Hartshorne at his word, it seems like just about any B-module structure will do. But something odd happens the more you play with these definitions.

We know that V = SpecB is an affine set, with f⁻¹(V ) = SpecA also affine, with A a finitely generated B-module. But now what you can do is restrict f to this open affine, and obtain a map of affine schemes:

f : f−1(V )	→ V
i.e. f : SpecA	→ SpecB

 

But we know that this map is induced by a particular map of rings.

 

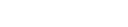Do you see the problem? I’m asking the laymen, not the mathematicians. For the layman, there is a huge technical problem that can result in your complete destruction. If you notice the problem, you might feel like you’re going insane. You are not, and it’s not your fault. Your feelings are valid. Here’s the deal: We know that A is a (B-algebra which is a) finitely generated B-module, which means that there is a surjection of B-modules

 

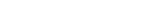induced by a ring map δ : B → A. But ϕ also induces an B-module structure on A. Do δ and ϕ coincide? They don’t have to, without stipulating. And what if the B-module structure induced by ϕ isn’t finitely generated, even though the one by δ is?



This is not your fault. Hartshorne simply didn’t bring the goods. I’m serious. Look elsewhere, and you’ll see the extra stipulation that the B-module structure on A must be the one induced by ϕ:




Yep. This is the correct definition: the part about the ring morphism is missing from Hartshorne, because apparently he thinks it just ”goes without saying.” It’s not, to the amateur: The B-module structure must be consistent with the ring morphisms induced by f.


Now see that little citation?







.......................



The student facepalms. Yet, that citation just proves that it was intended to ”go without saying.” So, hold on: Is there something similar wonkiness happening to the finite type definition? Let’s examine it again:




The question, of course, is which B_i-algebra structure? Again, we can restrict to a map of schemes

fi : f−1(V i)	→ V i
i.e. fi : ⋃ j∈JUij	→ V i
i.e. fi : ⋃ j∈JSpec(Aij)	→ Spec(Bi)

 

This time I have to refine and restrict even further, to get maps

fij : Spec(Aij)

→ Spec(Bi)

 

Which are of course induced by ring maps

ϕij : Bi

→ Aij

 

So we can only assume analogously that the B_ij algebra structures must be induced by these ring maps, i.e. they must be consistent with f. Is this ”obvious”? Does this just ”go without saying”? After the finite fiasco, you have to intuit that it is a part of the definition. Admittedly, it is subtle. For example, I was even using this assumption without realizing it in just a while back (note that to combine the generators together, I had to assume the B-module structures were consistent with each other–that the A_js did not have different B → A_j, which they don’t if they are induced from f). But it should be mentioned precisely because it is subtle.



In any case, with all that technical machinery in place, back to the exercise:  


Now this is trivial by taking one of the open affines V _i = SpecB_i that contains y, and reducing precisely to that affine case:

f : f−1(V ) = SpecA

→ SpecB

 

which is induced by a ring morphism

ϕ : B

→ A

 

And now the problem is pure algebra: Knowing that ϕ induces a finitely generated B-module structure on A, show that there are finitely many prime ideals Q of A such that ϕ⁻¹(Q) = y.

We know that ϕ induces a surjection

ϕn : Bn

↠ A

 

(this is where all that technical insanity comes into play. We need the finitely generated B-module structure on A to be induced by ϕ)

Every prime ideal in B has only n copies in Bⁿ. And taking quotients produces a bijection between the prime ideals of A and the primes of Bⁿ containing the kernel. So y corresponds to n primes of Bⁿ which corresponds to at most n primes of A. Done.

So now the utility of ”finite type” and ”finite” morphisms is a bit more clear: They are locally induced by extremely convenient ring morphisms.

And yes, that was all for part A. Suffice to say, We’re not touching B or C this week.

3.6

 

Finally. We get a brief bit of sun in the fog. First, as foreshadowed last time, we have a notion of a scheme being ”integral”:


Thar’s geometry defined directly according to algebra. Turns out, integral schemes are irreducible:


Which means that, according to the moth, we can in fact furnish Hartshorne’s desired ζ: You can conquer the world, if it is irreducible. Since the closure is the whole space, every open set contains it. Furthermore, the moth tells us that, given an open affine, ζ is, in fact, a generic point of SpecA. So given U = SpecA ⊂ X, ζ ∈ U, and furthermore, 𝒪_ζ,U = 𝒪_ζ,X. But 𝒪_ζ,U = 𝒪_ζ,SpecA = A_ζ. Now, ζ being a generic point of SpecA means that it can be seen as a prime ideal of A contained in every other prime ideal of A contains it, so 0. And since 𝒪_X(SpecA) = Ais an integral domain, via integrality of X, then ζ must be (0). So our local ring is just A₍₀₎, which is the standard definition of the quotient field K(A).

So Hartshorne’s prescribed order of business was misleading (Moral: Hartshorne is not very trustworthy). We dropped down to affines and snagged both birds with one stone. Listen to the moth. I’ll tell you: The Schoolmaster’s withholding some spoils for us again. He’s not talking about the bigger implications of this. Indeed, there’s more to be had here, so let’s sniff some of it out from some old crumbs. Is it odd that K(X) = K(U), even though U’s an open subset of X?

Longtime readers may recall the age of birational equivalence, back in varietyland. In particular:


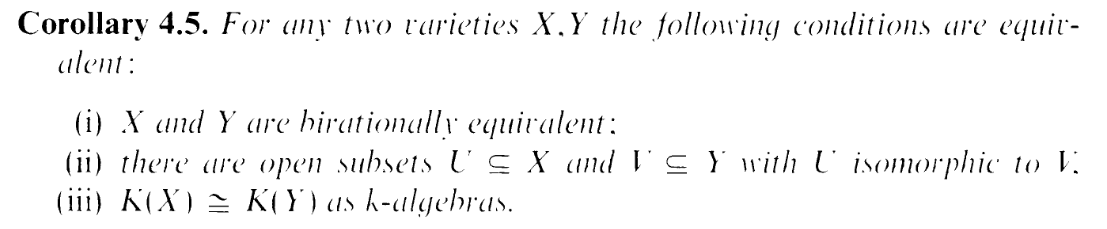
A big reason this ”worked” on varieties is due to varieties being irreducible, from which follows the density of their open sets. Likewise, integral schemes are irreducible, from which follows the density of their open sets. The density allows us to equate the function field of the whole with the dense set.

Now, peeking ahead a bit, birationality appears to ”fail” on schemes in general:

However the generalization is very elegant in the language of generic points:



Birationality is a philosophy. It is the great point theory. You equate a few generic points to determine entire schemes–the more irreducible the better. Why study huge masses of points when the great local few really hold the forks? The world aint impersonal. The world moves. The temperaments of zetas and etas determine the P’s and Q’s. In war, men are nothing; one moth is everything.

3.7

 

Boys, sometimes you gotta act like you know what you’re doing if y’wanna keep your heads on your shoulders. In other words, I have no clue how to do the first half of this exercise, but I’m going to do the second half and call it a day, and we can circle back with an errata later if we please. Indeed, I bluffed and puffed through 3.4 too. Ha ha ha! In any case, why is K(X) a finite extension of K(Y )? Something to do with generic finiteness and dominance. I don’t know. We’ll just assume it is, and take that as our starting point. Let U be any open affine subset of Y . Then, thanks to finite-typeness, f : X → Y restricts to a map:

f : SpecB

→ SpecA

 

where via integrality, I know that A and B are integral domains, which means that (0) is a prime ideal in both A and B, and furthermore g((0)) = (0), so there is a map of local rings which can be written in a multitude of ways:

A(0)	→ B(0)
K(A)	→ K(B)
K(SpecA)	→ K(SpecB)
K(Y )	→ K(X)

 

The main point is that the quotient field K(B) is a finite extension of the quotient field K(A). Now the question is: Can we finitely generate B as an A-module? (A and B integral domains). Note: I’ve reduced to a pure algebra problem, again. Let’s proceed.

Let b₁∕c₁,…,b_n∕c_n be ”modgenerators” for K(B) (i.e. generate K(B) as a module over K(A)).

Then given b ∈ B, I would like to modgenerate it over A. Now I can modgenerate b using the modgenerators of K(B), but I’m going to actually instead use them to modgenerate b∕(c₁ c_n). You’ll see why (Note: of course, I initially generated b and had to backtrack midway through the proof when I realized I needed b∕(c₁ c_n). I don’t have magical intuition). Let c = c₁ c_n for simplicity. Then

⋅ + + ⋅

= b∕c

 

where the a_i,d_i ∈ A (I can assume the d_i are noninvertible). Now I’ll multiply out the c_i denominators to obtain

[c2 cnb1] + + [c1 cn−1 ⋅ bn]

= b

 

(that’s why I generated b∕c instead of b). This is progress. The elements in square brackets constitute modgenerators in B (rather than K(B)) for our arbitrary b. But we are still modgenerating over K(A) rather than A. Now I want to get rid of the d_is. So let me multiply them out

a1d2 dn[c2 cnb1] + + and1dn−1[c1 cn−1bn]

= bd1 dn

 

Uh oh. Too greedy? We added a bunch of factor mush to the b. But we’re actually safe, because we can cancel out the d_is. Does that seem crazy? It’s not if we’re in an integral domain. Let me show you how to cancel out the d₁, for example. Note that on the left hand side, every term seems to have a factor of d₁ except maybe the first. To emphasize this, let me rewrite the above as

a + d1[e2] + d1[e3] + + d1[en]

= bd1d2 dn

 

Now I’ll subtract everything except a from the left hand side

a	= bd1d2 dn − d1[e2] − d1[e3] − − d1[en]
a	= d1(bd2 dn − [e2] − [e3] − − [en])

 

This equality says that that a must have a factor of d₁. And since we’re in an integral domain, cancellation holds. Just a little bit of more technical material, to make sure our cancellation is ”safe.” Reexpanding our a:

 

if I cancel out a d₁, am I ”harming” my modgenerator in the bracket? I want to leave that intact. Since I am lazy, I’m just going to go ahead and add extra generators. That’s right. My generators are just going to be every product I can form from members of the set {c₁,…,c_n,b₁,…,b_n} (without replacement). That’s still a finite amount, so I’m safe (albeit generous).

Promontories

So, we’ve performed not a perfect but nevertheless functional walk and stress test through these folks:

1. locally finite type
2. finite type
3. finite
4. quasi-finite
5. generically finite

 

And now, how are we going to get around the rest?



Here’s my report so far, Mr. Representative: It’s a foggy mess. Yep, yep. At this rate, the case of fiber products are doomed. Split forces. COMMANDERS GUNNING FOR RED HOT SHOT ON THE FLEET OUT OF RANGE; GUNNERS TRYING TO COOK THEIR SHOTS ON HOT POTS. Sniff. Y’can smell sweet onions next to the failed battery. We have no furnaces, man. The scant material we meekly begged out of the countryside are all WHACK: Mortars mismatched with shot, rimbaseless trunnions, gaugeless guns. And many of our poor little geometers are hungry and shoeless. It’s little appreciated in the leadership how these little fairfaced youngsters are volunteers, self-learners, idealists scooped up in the mass levy. And even the more experienced aren’t taking the time to train em. This organization isn’t ripe for imparting expert knowledge unto the layman. MR. REPRSENTATIVE: Our crews are unintimate with their schema, cuz the leadership trades the pieces around like cards: Eight motley men procured a new wagon, and attempted to secure the gun on the caisson and their boxes on the limber. The system or even notion of base schema is absent. The poor little geometers weren’t told which structure their algebras and modules were to take, and thus they’re left firepowerless in matters of finiteness. Yes: The Ol’ Schoolmaster is the Ol’ Unreliable on matters of theory, glossing over the minute details and brushing away technical matters that resolve ”naturally” to an academic mind. What’s a layman to do? Can you blame one of these poor fools for trying to use a sponge as a ramrod? For mixing up a vector space with a module, or a module with an algebra? The studious student facepalms. No theory is driven into them, so axiomatic if they are to become accustomed to new pieces and carriage. Their commander had a lucky streak on the path here along the coast, and is now comfortably billeting back inland. But I’m not going to leave these poor youngsters to themselves. I’m one of em. I’ll go sleep with em on the frontlines. I’ll supervise their battery constructions beyond the white line of doom. I’ll stand strong on the rampart in full view of the cannons pointed at us.

I’ll teach them the technicalities. I’ll lay down the law.