II.3.9
3/18/2022
But every week’s a bad week of hither in the gray season. Action without
direction under unorganized units and split forces–or rather awful inaction and
indecisiveness. We had no viable siege artillery, nothin’ more than field brass
4pdrs. But while our commanders are dragging their feet over the critical
promontory, I decided to get something on the floor: Sketching out finiteness, and
building up to our first battery: So we made an exhausting, depressing trip along
the coast, sighting old iron ordnances standing lone and apart, muzzles pointed
aimlessly into the sea. What did the boys feel when they looked upon them?
Regret, frustration. Those superheavy mortars from another time, those
cannons imprinted with fleur-de-tensors: Did they intimidate our boys?
Demoralize them? With the lack of supplies coming in from the capital,
they felt like no-good scavengers of the royal regime they so confidently
renounced. These cannons, so old and esoteric in operation, unfriendly to their
soft touch. Abandoned by veterans of the disbanded coast guard who
were so intimate with the machinery, now to be manned by a bunch of
amateurs? Hah! WHERE ARE THE PRIME IDEALS? God, why are they
so confusingly emergent? So sparsely spaced? These aint our piece of
cake. These low ass naval carriages were meant to be assed back and
forth tween reasonable readjustments, not on a long lugged journey along
the coast. These cannons were meant to sit on their coastal thrones for
ages, bequeated unto the son’s sons of coastal folk and taken close care
of for generations more, looking out onto the horizon for the
figures of ghostly frigates. And we’re just going to snag em like thieves?
We’re going to uproot them from their ideal positions and take them for
ourselves? The boys felt awful. Illegitimate. Scavengers. Unroyal. And
they felt it more when they struggled to lug them back over the long
journey to our park. In all their iron heaviness, their naval making, their
ancient awfulness, it was an awkward, frustrating, infuriating journey to
bring them here. I wrangled a group of reluctant youngsters
to set up a basic battery along the northern side of the harbor. Then in
the frustration figuring out the kinks of these iron beasts, awkward
swinging them along the rails of the traversal carriage, taking breaks to
stare out at the Aurore and other ships of the line gathered on the Rade,
they started to realize: They were setting up these guns on the
harbor, overlooking the coast to aim at great ghostly frigates in the gray.
They were handling the coastal artillery of which they felt so underneath.
Back in varietyland, it was once boldly declared:
I am going to skip anything that makes me deal with the
tensor product.
Now, follow along. The (fiber) products of schemes are defined according to the
usual universal property:

Do these products exist in schemes? The answer is yes:
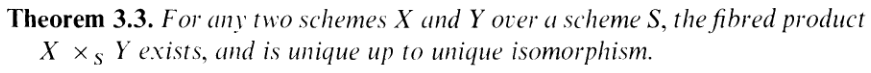
What do they look like? If all is affine, then:

Indeed, if all is affine, we have
 |
Yes. You’re reading that correctly. That’s a ⊗, not a × on the right. The product
of affine schemes (over an affine scheme) doesn’t derive from the product of rings,
but the tensor product of rings.
So, what’s the big deal about tensor products? Tensorphobia? Here’s the thing,
friend: A tensor product T is simply universal in that any billinear map from
A×B to S factors uniquely through T into a linear map into S. Hahahaha, just
kidding. Well, so the intuition lies in billinearity, fine. But that sort of abstraction
is not enough for us. We need to get down and dirty. What does A ⊗SB look
like?
The basis elements of A ⊗SB look like this:
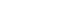 |
where a ∈ A,b ∈ B. (I will often drop the S in ⊗S, by the way)
But be careful: I said basis elements, not elements. That’s an easy mistake to
make. By that I mean, the general elements of A⊗SB are actually finite sums of
such basis elements:
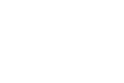 |
What you see above is an arbitrary element of A⊗B. Now, what’s strange about
this to the layman? Personally, it is extremely tempting when I see
a1 ⊗ b1 + a2 ⊗ b2 to try and ”add” them together to make a single element
a⊗b. In general, this is not possible. You can add a1 ⊗b1 and a2 ⊗b2, but this
sum cannot be ”simplified” in general. It is just a1 ⊗b1 + a2 ⊗b2. Here’s when
you can combine elements:
| a ⊗ b1 + a ⊗ b2 | = a ⊗ (b1 + b2) | ||
| a1 ⊗ b + a2 ⊗ b | = (a1 + a2) ⊗ b |
The motivation, again, is that the addition is ”billinear,” if that matters. Also,
given s ∈ S, you can multiply it in (since A and B are S-modules):
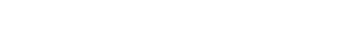 |
And finally, in our case we’re actually working with tensor products of algebras, so
we can do this:
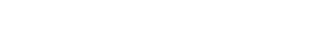 |
And that’s tensor math. These operations make it a ring (an S-algebra).
Now that we’ve gone through these operations, tensor math doesn’t seem all
complicated. Tensor products aren’t so unworkable on their own. Their
algebraic structure seems to be decently workable. What’s the big deal?
3.9: how2 fiber product

This exercise sums it up: We’re not doing algebra, we’re doing algebraic
geometry. Since these are rings, we’re interested in taking the spectrum of
them:
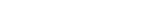 |
That gives us the fiber product So the important question for us geometers is:
What are the prime ideals of A⊗SB? This exercise says that there is no good
way of computing the fiber product in general. The fiber product
SpecA ⊗Spec
SSpecB can, in fact, look very different from the individual
spectra.
So what do we do?
I am going to skip anything that makes me deal with the
tensor product.
Facing your fears doesn’t mean fearlessly walking into the mouth of the beasts: That’s how you get shot. It often means grumbling and complaining, swalling your terror for little instants where you poke the bush and leap back in pathetic panic at any rustling (caused by yourself). Awkwardly lugging it along the coast, struggling to set it up, taking stupid breaks, and realizing after a day’s work that you’re done. In fact, they key to tensor products is hiding from them. I’m not kidding. Just watch.
A

So, since Ak1 ≃ Speck[x], and Ak2 ≃ Speck[x,y], this problem is just the
algebraic problem of proving
![?
k[x ] ⊗k k[y ]≃ k [x, y]](IIp3p96x.png) |
So here’s the map I’m going to use:
| ϕ : k[x] ⊗kk[y] | → k[x,y] | ||
| f(x) ⊗ g(y) |
 f(x)g(y) f(x)g(y) |
That’s right. Just multiply the polynomials together. Now, this may raise
some alarm bells: How do we reach elements that can’t be separated into
products of single variable polynomials? E.g. xy − 1 is irreducible, we can’t
separate that into ”polynomial in x times polynomial in y.” But you have to
remember: I defined the above map on the basis elements. The more general
elements are sums of basis elements. So we can reach xy − 1, like so:
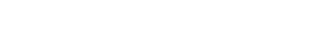 |
The main insight is that any polynomial in k[x,y] can be experessed as
the sum of monomials. In other words, our inverse map looks like this:
| δ : k[x,y] | → k[x] ⊗kk[y] | ||
| ∑ i=1nβ ixaiybi |
 ∑
i=1nβ
i(xai ⊗ ybi) ∑
i=1nβ
i(xai ⊗ ybi) |
In a sense, what we’re saying by making this isomorphism is that ”polynomial
rings are linear combinations of monic monomials.” Quite elegant.
Note, we computed the fiber product not via any categorical tensor philosophy,
but by comparing it to a more familiar, ordinary ring. We hid from the
tensor product–or, rather, we hid the tensor product under another ring.
B

So, we are computing the spectrum of R = k(s) ⊗kk(t). Clearly
| k(s) ⊗kk(t) ≃ k(s,t) |
via an analagous argument to A, so we are computing the prime ideals of k(s,t),
which is a field, making it a singleton.
....which makes no sense because the exercise is asking us to show it’s not a
singleton.
GOOD CATCH, YO: Catch the author’s intent, and correct yourself accordingly.
Here’s the thing. We do have an inclusion given by
| ϕ : R = k(s) ⊗kk(t) |
 k(s,t) k(s,t) | ||
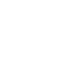 ⊗ ⊗
 |
 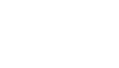 |
However, this inclusion isn’t surjective. You can add numerators, but you can’t
add denominators, so while this map can reach something like st − 1, it
can’t reach something like
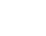 . What we have is a subring of k(s,t)
where we can only divide by elements that are separable into f(s)g(t).
. What we have is a subring of k(s,t)
where we can only divide by elements that are separable into f(s)g(t).
So what are the prime ideals of k(s) ⊗kk(t)? Seems like a difficult problem. The
answer is, of course, deal with her directly.
Here is an absolute gem that Yours Truly found lying on the coast:
if k is commutative (ring), R and S are commutative k-algebras such that R is
noetherian, and S is a finitely generated k-algebra, then the tensor product
R ⊗kS of R and S over k is a noetherian ring. (*)
In our case, k(s) ⊗kk(t) is what we’re dealing with. k(s) is a field, so it’s Notherian, and k(t) = k[t, 1∕t] is a finitely generated k-algebra. k(s) ⊗kk(t) is a Noetherian ring. In other words, I know that all its ideals are finitely generated. Notherianness has been dry in the past, but here’s where we get to see some of its power.
Because now we know that an arbitrary ideal is in the form
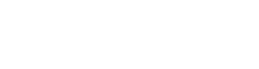 |
But clearly, the denominators of the generators can be removed and we still
get the same ideal. So I can in fact assume the ideals are in the form
 |
Furthermore, I can assume that the fi is factorable into irreducible polynomials
g1(s,t)
 gr(s,t) because k[s,t] is a UFD. And furthermore, each of these
gis have both s and t terms (otherwise, I could just divide them out)
gr(s,t) because k[s,t] is a UFD. And furthermore, each of these
gis have both s and t terms (otherwise, I could just divide them out)
But this begs the question: How do these ideals relate to those of k[s,t]? Time
for a lemma.
0.0.1 Lemma
If the ideal I generated by f1(s,t),…,fn(s,t) (with the factorizations above) in R is prime, then the ideal J generated by the same elements in k[s,t] is prime
Proof
suppose f ⋅g ∈ J. Then trivially f ⋅g ∈ I. Since I is prime, we can assume wlg
f ∈ I. So
| f | =
 f1 + f1 +
 + +
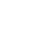 fn fn |
As we’ve done many times, we’re going to multiply out the denomiators (note this
trend when we try to extrapolate ”local” properties to ”global” ones):
fh1
 hn hn | = g1h2
 hnf1 + hnf1 +
 + gnh1 + gnh1
 hn−1fn hn−1fn |
Like last week, I claim we can cancel out the hi etc. to isolate f, but again I want
to maintain the generators f1,…,fn. E.g. canceling out h1 maintains f2,…,fn,
but does it mess with f1? The answer is no, because h1 is in the form
g(s)h(t), and we assumed that none of f1s irreducible factors are in that
form.
QED
So since all the prime ideals of k[s,t] are generated by irreducible elements
anyway, we can compute the prime ideals of R by simply looking at the prime
ideals of k[s,t] and weeding out the ones that don’t work.
If any of the (irreducible) fi is in k[s] or k[t], then this isn’t a prime ideal of R,
since we can divide by fi and produce the unit ideal. But that’s it. The prime
ideals of R are the prime ideals of k[s,t] whose generators can’t be divided out:
i.e. are given by irreducible polynomials that have both variables in them. So, e.g.,
(st − 1) is makes a prime ideal in R, but not (s − a) or (s − a,t − b), etc.
Again: We dealt with the tensor product k(s) ⊗kk(t) indrectly: by appealing to
k(s,t) and especially k[s,t].