Apologies for the broken links in the last post. I have fixed them. Now I just have to fix my broken heart </3.

"What happened to 3.14?" It broke my heart. Well, every exercise breaks my heart. The holeinmyheart just gets bigger and bigger. Soon, it will be wide enough for some very fancy ero guro.

Listen: 3.14 has to do with two of my worst topics on this blog. Part (a) has to do with linear algebra. And part (b)? Here's something funny. After a day's worth of struggling my butt off in the "easy" world of linear algebra, I decided that it might be time to give up, and then I realized that I actually had not read part (b) yet. I took a glance at it, and what do I see? I'll just give you the abbreviation:

Hmmm, what could it be? Trading Card Came? Tnu C Compiler? Titty Cocky Cunny? All excellent guesses, but not quite right. The "longtime" reader will be able to fill it in. I am genuinely getting frustrated just remembering it. #throwback #holeinmyheartnostalgia

Today [written on Saturday] was a gigantic waste of a day. Sometimes, those are nice. Today, it wasn't. Well, in about 30 minutes, I'm going to go out for a walk again. Those are the things that temper the nothingness of a nothing day. Here's some advice, from yours truly:



You like that? While I'm at it, might as well give you another one:



Wow. I'm getting good at this. How did I come up with that one? I dunno. I think it's just my overflowing sense of empathy. Let me try another one.



W-wow. That was really inspiring, huh? I surprise myself sometimes. Maybe I should become a motivational speaker or something. Here's another one.



*BANG*

Oops, I malfunctioned for a bit, hehe. Now, reader, would you like to come along with me for a little date? *Gets closer* Why are you trembling reader? Too frozen in fear to move? Hehe, it's fine. You don't have to move. Just relax your muscles and let me take control from here. *Strokes your hair and smells it* Mmmm, strawberries. It fits you. Sniffffffffffffffff. Don't worry, reader.... I have this all under control.

Hey, hey. I'm just treating others how I would like to be treated.

Yes, I'm a little frustrated at my mathematical inability. Yes, I get rapey when I get angrey. However, I have to get something done, so here's part (a) and part (c) of an exercise.



PART (a):

Almost gave up on this one as well, in spite of the hand holding hint. So, they suppose that

and define

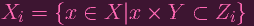First job is to show that X = X₁ ∪ X₂. Now clearly X ⊃ X₁ ∪ X₂, so we want to show that given x ∈ X, x is either in X₁ or X₂.

Yep. I got stuck here for hours. "Little early to get stuck, eh?" As early as my posting schedule is late, eh? Hahahahaha, *clings teacups*. Here's the thing: If x is neither in X₁ nor X₂, then that means that x×Y is contained neither in Z₁ nor Z₂. I.e.: this is the light bulb, x × Y can be split up. Can we use this "splitting up" to split up the irreducible Y and earn a contradiction?

Let's say that x = (p₁,…,p_n)

Let's also say that x = (p₁,…,p_n) and let's write the coordinate ring of A^n+m as k[x₁,…,x_n,y₁,…,y_m], and

Note two things:

(1)

(here Z is taken in A^n+m)

(2)

(here I is taken in A(A^m) and Z is taken in A^n+m)

Hence, intersecting (1) and (2) shows that x × Y is closed. So...

x × Y	= (x × Y ) ∩ (X × Y )
	= (x × Y ) ∩ (Z1 ∪ Z2)
	= ((x × Y ) ∩ Z1) ∪ ((x × Y ) ∩ Z2)
	= C1 ∪ C2

where C₁,C₂ are closed. Here's what I mean: If I can break x × Y up into C₁ ∪ C₂ closed sets, it seems that I can break Y up into D₁ ∪ D₂ closed sets. Here's how I'll do it. Given f ∈ A(A^n+m), let me define

I.e. I plug in x into f to get a polynomial in k[y₁,…,y_m] (I am transferring a polynomial function on x×A^m to a polynomial function on A^m), where clearly

Soo, let me set

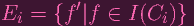And let D_i = Z_m(E_i) (writing Z_m(⋅) to denote that I'm taking the zero set in A^m here). And note:

x × y	∈ Ci
⇐⇒f(x × y)	= 0(∀f ∈ I(Ci))
⇐⇒f′(y)	= 0(∀f′∈ Ei)
⇐⇒y	∈ Zm(Ei)
⇐⇒y	∈ Di

So now I can write C_i = x × D_i. Hence,

x × Y	= (x × D1) ∪ (x × D2)
	= x × (D1 ∪ D2)
Y	= D1 ∪ D2

Yaaaaaaay!

Proving that X₁,X₂ are closed is "easy". Since

Z_i is clearly generated by polynomials that have no Y terms, and these polynomials determine X_i.

PART (a) done.

NOW, you might be wondering why I am skipping part (b)? Well, what's wrong with part (b)?



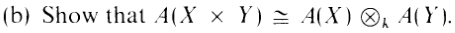
Hmmm? What's that symbol over there? That's a fancy looking little symbol, eh?



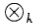
Oooooh, very cute. It's like a multiplication inside a circle. And a little k nestled up on the side. Very interesting. Would you like to know what my reaction to seeing this symbol is? Here it is:

This happens to be the symbol for the tensor product. I have already whined in this post about linear algebra and the TCC, but listen: A while back before I started this blog, in my pathetic flails in an attempt to learn math, I had dealt with the tensor product. All I'll say is...

I am going to skip anything that makes me deal with the tensor product

At least for now.



PART (c):

On the other hand, I can do part (c), even though it involves the tensor product. That is be cause I don't actually have to look inside the tensor product. In my math-flail-learning history, I acquired a very basic knowledge of category theory, and I can use that to meme this question out.

In the text there is a corollary:



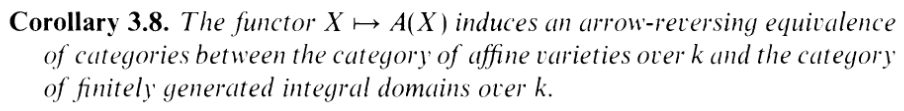
Since we have an arrow-reversing equivalence of categories, saying that X ×Y is a product is equivalent to saying that A(X × Y ) is a coproduct, which it is, because the tensor product A(X) ⊗ A(Y ) is a coproduct . If you have no idea what the fuck I just said, don't worry, me neither. It's just abstract nonsense.

Part (d) requires me to look inside the tensor product, hence I am skipping it. Seeya next time!