I.3.15ac_ERRATA
5/15/2021
Ahhhh, the smell of errata in the morning. 'Tis been a while since I've casually
stated a false statement and not gotten away with it. Let's take a look.
Since
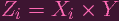
Zi is clearly generated by polynomials that have no Y terms, and these
polynomials determine Xi.
Firstly, I meant to say "no yi terms". There is no such thing as a "Y " term, since
Y is a variety, not an indeterminate in a polynomial ring. Secondly, that would
still be wrong. Let's try this again.
Let f ∈ I(Zi). Define
 |
(i.e. analogous to before, plug in y for the yi coordinates and leave the xi
coordinates as indeterminates, giving us a polynomial in k[{xi}]. We do this for
every y ∈ Y ). Then
| x | ∈ Xi | ||
| ⇐⇒x × Y | ⊂ Xi × Y | ||
| ⇐⇒∀y ∈ Y : x × y | ∈ Zi | ||
| ⇐⇒∀y ∈ Y,∀f ∈ I(Zi) : f(x × y) | = 0 | ||
| ⇐⇒∀f ∈ I(Zi),∀y ∈ Y : f(x × y) | = 0 | ||
| ⇐⇒∀f ∈ I(Zi),∀g ∈ Sf : g(x) | = 0 | ||
| ⇐⇒∀g ∈⋃ f∈I(Zi)Sf : g(x) | = 0 | ||
| ⇐⇒x | ∈ Z(⋃ f∈I(Zi)Sf) | ||
That last set is closed, so Xi is closed. So that's fixed.
Also, boy, I am slowing down in updates again. The ebb and flow of Hartshorned is mysterious, dependent more on your dear admin's whim than their actual busyness. A new week is upon us, let's see how we do.