Welcome to the month of March:





Hahaha, how cute. We’re learning our first properties of schemes!!!!!! Smell the flowers: NOW, LITTLE GEOMETERS, Ol’ Hartshorne on the dais sermoning, we untie our shoes and dip our toes into the maroon seas a bit more: Is it cold? Tensor products and such? HERE’S SOME MOTIVATION: ”the intersection of algebra and geometry.” OOOOOOOOOOO. We transfer integral domains into geometric integrality. OOOOOOOOOO. We can purge all the ugly nilpotencies to reduce our geometry. OOOOOOOOOOOO. We take up Noetherianness (for a scheme proper), and define the notion of subschema more explicitly. OOOOOOOOOOOO. And, finally, the obligatory construction of products. OOOOOOOOO. That’s the deal. Shall we march into March, fair youths? ARE YA UP FOR IT, MY CUTE LITTLE GEOMETERS? A silence, yielding to the ambience seeping in through the open windows–ambiguous breeze, birdchatter and humansong. The longing to escape, to be out there and exist. Something’s missing. Something feels off. Schemes? Is that it? Schemes n schema? The world outside is out there and yet here we are inside in this ornate, stuffy room, locked up looming over our desks while we are loomed over by the pulpited Schoolmaster, himself loomed over by stately columns pilastered with designs of densely intertwined calligraphic F’s and O’s, and a titanic statue after Grothendieck. What does he see? How does he decipher the writing on the walls? It’s crispy out and crusty in. Clickety-clack there and claustrophobic here. You get to choose your friends, but neither your family nor seatmate. Look at the lad next to you: That is your partner-for-life. Breathe him in: Till Nature, as she wrought thee, fell a-doting. Smell the flowers. A student sneezes. The Schoolmaster facepalms. It’s spring yo. Nah, I’m just allergic to boysmell. A-ALLERGIC TO B-B-BOYSMELL????? Sneezes in pederasty. The pupil hears a Mockingbird. Ahhhh, how I would untie my shoes and walk into Arcadia. But Algebraic Geometry? The mad master wags his finger at the mad wag in Adagio, ma semplicemente: IF YOU HEARD CANNONS ON THE PLATEAU YONDER? WILL YOU GO OUT AND BECOME ITS FODDER? ARE YA PREPARED TO NEVER HEAR THE BIRDS SING AGAIN, PUNK? CAUSE IF YAINT LEARNED, YOU’RE FRONT ROW VANGUARD, BUT: You have a point. We aren’t in the times of Caesar. Nowadays, an artillery commander has to venture within grapeshot holding a Tricolor-bullseye, taste blown up flying dust, subjugate himself to near misses and good scares. He has to be in the zone. Take risks. Interact with the field. And so the Schoolmaster disembarks from the dais and paces from column to column, and all the boyish faces look up at his head, summer’s green all girded up in the sheaves of his bristly beard, sticking out and bobbing about like a sore sailboat in the vast chalkmarked black sea. And standing some feet from the left column, he stops in an impeccable rehearsed scene: the Schoolmaster in Agitation, finger wagging his own chin, dwarfed by that togaclad giant statue of Grothendieck erected in the same posture, carefully planning when and how to present the truth–to impart the revolution unto a new summer and distill himself in the youth before him before it is sniped away by passion-quibble. What is algebraic geometry about? SCHEMES, the class replies. Wrong, he answers, you are all wrong. As the class shuffles in bewilderment, looking up again at this month’s title, so innocently written: FIRST PROPERTIES OF SCHEMES. Is that it? Is that Algebraic Geometry? As we move forward, you will start to realize something much deeper is going on. Is it really just Schemes n Schema? Or... is it.... ______ n _____? He starts maniacally laughing, and so does the statue of Grothendieck.





Check this out:


A property of a morphism, rather than a scheme. HINT, HINT, FOR THE FUTURE, REGARDING THE LECTURE ABOVE. In any case, let’s casually move forward. As Hartshorne states, we begin with a batch of exercises that give us alternate criteria that, at times, might be more convenient to test the finiteness of morphisms.

Unfortunately, Yours Truly only brings y’all one exercise this week, as most of the week was spent reading Schoolmaster Hartshorne’s exposition and getting demolished on products. If you want to see me screaming, wait till we get to an exercise with products. But for now, something simpler:

3.1

 

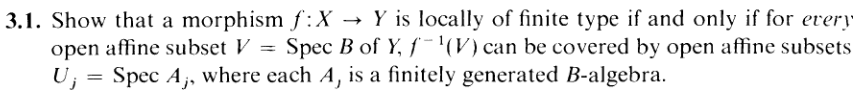
The ”if” is obvious, so we need to deal with the ”only if.” We assume f : X → Y is locally finite type, so give me an open affine cover of Y :

 
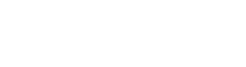such that for i ∈ I:

 
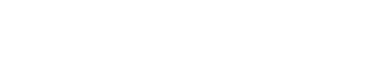where each A_ij is a finitely generated B_i-algebra. (Wikipedia’s definition of a finitely generated algebra works here if you allow replacing K with any ring).

Now I’m going to let V = SpecB ⊂ Y be an arbitrary open affine. In that case, using some basic set theory:

f−1(V )	= f−1(⋃ i∈IV ∩ V i)
	= ⋃ i∈If−1(V ∩ V i)
	= ⋃ i∈If−1(V ) ∩ f−1(V i)
	= ⋃ i∈If−1(V ) ∩ (⋃ j∈JiUij)
	= ⋃ i∈I ⋃ j∈Jif−1(V ) ∩ U ij
	= ⋃ i∈I,j∈Jif−1(V ) ∩ U ij
	= ⋃ i∈I,j∈Jif−1(V ) ∩ Spec(A ij)

 
Now if each f⁻¹(V ) ∩ Spec(A_ij) could be expressed as the spectrum of a finitely generated B_i-algebra, we’d be done. However, even though, Spec(A_ij) is the spectrum of a finitely generated B_i-algebra, I cannot guarantee that an arbitrary open subset of is also one. HOWEVER: I can guarantee it for any basis element D(f) in it, as you will see shortly, and that is sufficient as we can just refine the open cover above to such basis elements. So proving the following Lemma will clearly finish this exercise off:

0.0.1 Lemma

Let X = SpecA where A is a finitely generated B-algebra, and let U be open in X. Then U has an open covering of spectra of finitely generated B-algebras (in fact, this open covering is an open covering of D(f)’s).

Proof

Since A is a finitely generated B-algebra, we have a surjection

 
Now let D(f) ⊂ U. Then 𝒪_X(D(f)) = A_f. And ϕ extends to a natural surjection

 

QED

Yea, that’s it. More next week.