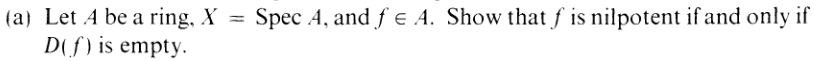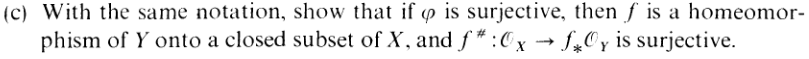Ah, breast! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! BREAST! Yes, I’ve taken up a mistress–wife of a lieutenant. I sent him out on a scout, when he was intercepted by unfriendly frigates and returned redfaced. He threw a precious glass of Asti at me and I caught it and drank it. He wasted another one on his wife, and his wife couldn’t dodge: She bled blood and red wine from her forehead, like a soldier headshot in war. And when she later posed for David she tried to hide the scar with her auburn hair, and he said this: ”No, part it.” That sparked something perhaps: They shared a dream. Something about a dead man in a hearse. No, he was in the hearse. No, he played with her passions. No, it was very confusing. No, he wasn’t supposed to commit to a girl like her. He had another one that took off on him like a statue. He undid all his dignity and splayed himself wide open for that one, and it stared back like a statue. He committed to continuing that pursuit out of spite. She was fruitless, but God, wasn’t that it? What did he do? He instantiated his devotion to that object based on certain characteristics it presently possessed, and maintained that devotion in independence of the variation in those characteristics thereafter. Bloat her, rip off half her hair, flick off a tooth, and it sticks. Dilute the serenity and selflessness, and it sticks. That’s a rigid designator–a proper name: causally connected to that object and, maintaining that that conjunction held in natural consensus and intuition, it was that same object referred to by that name–”I'm infatuated with Sylvia”–that would forever be bound to his want. For as a name can be bound to an object, so can love be bound to that name. And suppose you come across another one whose characteristics match those that instantiated the binding more perfectly? It wouldn’t matter, because it was the binding, not the characteristics, that mattered. And yet, here he was, walking down alone what he liked to call the Rue de Lucky Shot pitch black past curfew, marvelling at the arrogance of none other than himself. In the arms of a whole different lady: A whole different beast–a whole different character, in fact. A new world in the foundation of situation and circumstance: A divorcee. Something tackling abstractness–down to Earth–consequential, and somewhat necessary. Something incongruent. Tessie. Tessie. Tessie. Wasn’t any Cupid’s arrow a ”lucky shot”? He was pierced by the stare of Sylvia–L’Inconsalabile. And he tried to abstract the principle of that thing into something that extended beyond himself, and the deeper he looked, the more he saw the cracks written in the stone: The chipped crown; blemished nose; permanent perplexion; the irreconcilable awkwardness of position and proportion when overscrutinized; the reductionism of the concept into its grains and phenocrysts; the voided, irisless eyes staring through and beyond him into the vast emptiness of nothing. That was the ideal: form on form. But it began with a shot. It began with a bang. And then there was Tessie: Who posed for him, dressed Moorish and Japanese and nude and red and gold. Whose arms responded to his own in mutual embrace. Whose complexion changed depending on the extent to which she had groomed herself. Who was perplexed, then panicked, then reassured. Who wedded once and was now alone. Who uprooted idealism. Tess in the flesh. Fleshy Tessie. Who gave him touch. BANG! Was this it? Strolling down in the dark, where all the grandeur blurred into vague nightly figures, and yet: Miles from Rivoli itself, he could still feel the echoes of those two Austrian ammunition wagons exploding and the tides turning. He could feel it, moreso than he could fashion feeling 20 years of humble, hermited, hamleted living in the Romantic countryside. Moreso than any ascetic, pastoral dream. Who was more foolish? The one who rested on the laurels of their lucky shot? Or the one who latched onto their lucky shot and didn’t let go like a horny pig, and furthermore interacted with it, exploited it, demanded more out of it? Tessie ruled all. The irreconcilable awkwardness of position and proportion–irreconcilable, of course, since humans are creatures of motion. The world isn’t static. The world moves. White on white. Yellow on yellow. BANG! I killed waifuism. Ha ha ha ha ha ha. After having wasted seeds on seedlessness, his revelation on that dark, empty street was nascent, when he spotted a vague figure standing on the wayside facing him. He suddenly felt dread cuz it was a man and the man approached him slowly his torso swinging left and right and he couldnt move or anything cause he hadnt learned how and and the man stood over him like a grandfather clock and said

2.18

A

B

injectivity on sheaves

So we want to show that

 
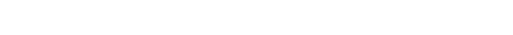As a reminder, f^♯(V ) can be seen as a restriction of a map

 
given by composing with ϕ_P’s. This makes the ”only if” trivial. As for the ”if”: Prop 2.2 tells me that if I let V = X in the above, I simply recover ϕ, so it’s injective.

Dominance

So now I want to show that injectivity dominance.

1. To show that f(Y ) is dense in X, it suffices to show that every nonempty open basis element intersects it.

Let U = D(g) be a nonempty basis element. BECAUSE OF A, we know that g is NOT nilpotent.

Now to show 1, we’re looking for a prime ideal P of X such that

1. P ∈ f(Y ): i.e. P = ϕ⁻¹(Q) for some prime ideal Q of B
2. P ∈ U: i.e. P does not contain g

So we need to get P from Q. And a natural choice for Q would be an analogue of 2: Let Q be a prime ideal of B that doesn’t contain ϕ(g). Does one exist? Well, if every prime ideal contained ϕ(g), THEN IT WOULD BE IN THE NILRADICAL. Wait What? Yep, See here! (THAT PROOF USES ZORN’S LEMMA) I.e. ϕ(g) would be nilpotent. ”Ooohh, does this contradict the nonnilpotency of g?” Let’s see:

[ϕ(g)]n	= 0
ϕ(gn)	= 0
gn	= 0	HERE’S WHERE WE USE INJECTIVITY
g	nilpotent

 
which is a contradiction. So Q DOES exist, and P = ϕ⁻¹(Q) satisfies our conditions.

C

closed subset homeomorphism

So we’d like to show

 
It suffices to show that f is a bijective closed map: Let g : Y → f(Y ) be f with restricted range. Then, first off, closedness of f means that f(Y ) is closed. And since f(Y ) is closed, g inherits continuity from f. And since it is bijective and closed, g has a continuous inverse. Therefore g is a homeomorphism.

So I’ll try to show f is closed. It suffices to show that f maps closed basis elements to closed sets. So let V (g) ⊂ Y be a closed set. I want to show that f(V (g)) ⊂ SpecA is closed, where

 
So I need a V (I) in SpecA that ends up equalling f(V (g)), and the most ”natural” thing I can think of is letting I = (ϕ⁻¹(g)) be the ideal generated by the inverse image of g. I can already get one side of the inclusion easy: If P ∈ f(V (g)), then P = ϕ⁻¹(Q), where g ∈ Q. But note that g ∈ Q ϕ⁻¹(g) ⊂ ϕ⁻¹(Q) = P, i.e. I ⊂ P, so P ∈ V (I). So f(V (g)) ⊂ V (I).

Now for the reverse inclusion: V (I) f(V (g)). Let’s say that P ∈ V (I), so

P	⊃ I
P	⊃ (ϕ−1(g))
ϕ(P)	⊃ ϕ((ϕ−1(g))) ϕ(P)	∋ g	(by surjectivity)

 
So, under certain conditions related to surjectivity (CONDITIONS NOT YET VERIFIED), ϕ(P) might in fact be a (prime) ideal that contains g. So what I am going to do is recover P by taking the inverse image of both sides:

ϕ−1(ϕ(P))	⊃ ϕ−1(g)
ϕ−1(ϕ(P))	⊃ (ϕ−1(g))	(Taking the ideal generated by both sides (LHS already an ideal))
ϕ−1(ϕ(P))	⊃ I

 
And the left hand side is a prime ideal. In fact, if I recover P on the left hand side, I’m done. And I know I can recover P because, following the cheatsheet, ϕ⁻¹(ϕ(P)) = P as long as ϕ is....





i....njective.......?

...........................................What?

But ϕ is surjective in this exercise..........

...............................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

 
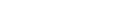Correct? Using surjectivity, we induce a ring isomorphism

 
Denoting π : A ↠ A∕ ker ϕ, we can view the situation like this:

 
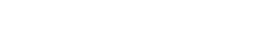which in turn induces

 
Yes, π^∗ is an injection, because every prime ideal of A corresonds to at most one prime ideal of A∕ ker ϕ. And noteworthily, it’s also continuous, so π^∗−1(SpecA) = SpecA∕ ker ϕ is a closed (clopen, even???a) subspace of SpecA. And the left side just says that f is in fact a homeomorphism onto this closed subspace. Done.

sheaf map is surjective

There’s a ϕ is surjective so it’s surjective locally i.e. f^♯ is surjective on stalks, therefore f^♯ is surjective.

D

 

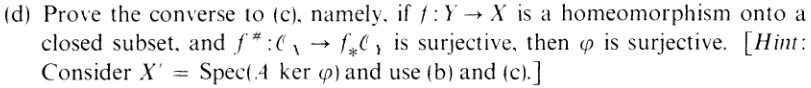
Something is very wrong here. What I’m going to do is decompose

 
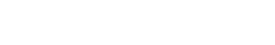So showing surjectivity at ϕ₁ would be sufficient. Now, I know that locally, given P prime in A, and denoting P′ = π(P),Q = ϕ₁(P′), this induces locally

 
But I know that ϕ_P is surjective because I’m given that f^♯ is surjective (and locally, f_P^♯ is just ϕ_P. Hence, that last map is a actually not just an injection, but an isomorphism. But although local surjectivity doesn’t imply surjectivity on sections, local isomorphisms imply sectional isomorphisms, and ϕ₁ is just the map of global sections, so we’re done.

Okay: What’s the problem? The problem is that I didn’t use the homeomorphism condition at all. So I made some huge error in my logic and I can’t find it.

2.16: A generalization of D(f)

 

So what is this exercise about? Well, we have those convenient D(f) = X −V (f) elements for affine schemes. This exercise is about trying to make a version of that, X_f, for general schemes. Affine schemes work pretty nicely, general schemes are more messy. X_f will be an attempt to give a bit of affine flavor to our scheme, using the help of stalks.

How well does X_f hold up? Not bad, although it’s never confirmed here if they make a basis (or even an open cover), and furthermore b,c,d tells us that it works better the more quasi-compact-y our scheme is (When I said last time that Noetherianness makes schemes ”nice,” this exercise is a GOOD reason!!!!!!).

Oh, also:

Hartshorne is WRONG!!!!! f_x isn’t the ”stalk”, it’s the GERM of f in the stalk 𝒪_x.

A: X_f behaves well on affines

 

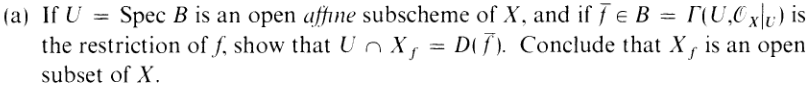
So X_f, when you restrict to the open affine sets, behaves exactly the way you expect: It IS a D(f) element.

If P ∈ D(f), then it’s automatically in U. So I’m going to assume P ∈ U, and prove

 
That’ll suffice.

Since P ∈ U = SpecB, I can view it as a prime ideal of B. Furthermore, since U is an open affine subscheme of X, 𝒪_P,X ≃𝒪_P,U ≃ B_P. Hence

P	∈ Xf
⇔ fP	𝔪P	(where 𝔪P the maximal ideal of 𝒪P,X)
⇔ fP	𝔪P	(where 𝔪P the maximal ideal of 𝒪P,U)
⇔ fP	𝔪P	(where 𝔪P the maximal ideal of BP)
⇔ fP	P ⋅ BP
⇔ fP	P	(← consequence of f ∈ B)
⇔ P	V (f)
⇔ P	∈ D(f)

 
SLICK, right? Now, here’s an obvious but VERYIMPORTANT CONSEQUENCE:

0.0.1 Lemma: If X is an affine scheme, then X_f = D(f)

0.0.2 Immediate from result, QED

SO BE WARNED. If X = SpecA is affine, we now have THREE ways of writing the same thing:

(1)

 
It’s definitely meaningful that each of these are defined in a different way under different contexts (one with stalks, one with sections, and finally one with pure algebra), but they are all the same thing in the lovely case of affines.

B

 

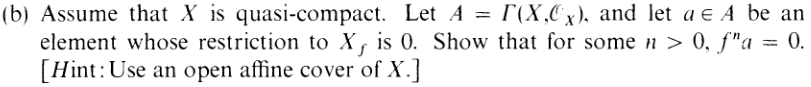
”WHAT are we doing here?” The key point to notice is that this is trivial for affines, precisely because of the equality (1) I mentioned above. fⁿa = 0 is simply how equality works in the localization A_f. IT’S JUST FRACTIONS, YO. We’re basically building up to part d which is to say, it all works out as expected for general schemes............. if they have enough quasi-compactness.

0.0.3 Lemma

If X an affine scheme, and a ∈ Γ(X,𝒪_X), then if a ∈ A such that ρ_Xf(a) = 0, then ∃n > 0 : fⁿa = 0

Trivial. QED

So no let’s suppose X is an arbitrary quasi-compact scheme and give it an open affine cover:

 
Denote a_i = ρ_Ui(a) the restriction of a, and f_i = ρ_Ui(f)). Then

ρXf(a)	= 0
ρUi∩Xf(a)	= 0
ρUi∩Xf(ai)	= 0
ρD(fi)(ai)	= 0	(A: Xf behaves well on affines)
ρXf i(ai)	= 0	((1))
∃ni > 0 : finia i	= 0

 
Now let n = max(n₁,…,n_l) (THIS IS WHERE WE USE THE FINITENESS OF THE OPEN COVER I.E. QUASICOMPACTNESS), so we can in fact write

 
for i = 1,…,l. Hence, fⁿa = 0 (since it restricts to f_iⁿa_i = 0 in each of the open affines)

C: Glueing Extravaganza

 

So, the wink wink nudge nudge in giving us quasicompactness on the intersections is that we need to glue together a bunch of stuff to create the element from A. Here’s how glueing works, as a reminder:


Now let’s start with the obligatory lemma for the affine case.

So consider the restriction of b ∈ Γ(X_f,𝒪_Xf) to U_i ∩ X_f, which I’ll denote

bi′ = ρD(fi)(b)

(2)

 
Now, since b_i′ is an element of D(f_i), I can write it as

bi′	= bi∕(fini)
finib i′	= bi

 
for some b_i ∈ Λ(U_i,𝒪_Ui) and n_i > 0. I’ll take n = max n₁,…n_l again, and replacing b_i : = f_i^n−n_ib_i, I can write

finb i′

= bi

 
where b_i ∈ Λ(U_i,𝒪_Ui)... So, really f_iⁿb_i′∈ Λ(U_i,𝒪_Ui). So these are maybe the elements we want to glue together.

Do they agree on the intersections U_i ∩ U_j?







Wait..... I have to do the same thing again for the intersections? But then that just creates an infinite recursive loop and I don’t even have quasicompactness at the lower levels....

........................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................

Third time’s the charm. This time, we’ll work from the ground up. I’m going to START with the intersections U_ij = U_i ∩ U_j, and since they are quasi-compact, I’ll give it an open cover:

Uij

= ⋃ k=1lijU ijk

 
Wow, the notation is getting really cumbersome and confusing, but there’s not much I can do about it without losing accuracy. I’m going to go ahead and let the restrictions of f and b be

fij	= ρUij(f)
fijk	= ρUijk(fij)
bij	= ρD(fij)(b)
bijk	= ρD(fijk)(bij)

 
(where D(f_ijk) = X_f ∩ U_ijk). Then by definition of the local ring, there is some n such that

fijknijb ijk

∈ Uijk

 
(I took n_ij = max(n_ijk)).

This is too much. There are too many indexes. How am I supposed to work with this?

I want to glue these guys into an element of U_ij. So now I want to check the... INTERSECTIONS OF INTERSECTIONS: U_ijkk′ = U_ijk ∩ U_ijk′. This is insane. What is this nonsense? To make things clear, I’m checking the equality:

ρUijkk′(fijknijb ijk) ρUijkk′(fijk′nijb ijk′)

 

AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

Okay:

ρUijkk′(fijknijb ijk)

 
NO NO NO NO NO NO N ON N O NO N ON O NO NO NO NO NO NO NO NO NO NO STUPID IDIOT STUPID IDIOT. I’M JUST HIDING FROM THE PROBLEM The problem is that I can show that the elements equal each other on U_i ∩ U_j ∩ D(f) but I cant show that they equal each other on U_i ∩ U_j more generally, because the b_i parts came from D(f) in the first place, so how am I supposed to make a more general statement out of that? I DONT KNOW, AND I’M JUST RUNNING AWAY FROM THE ISSUE BY TRYING TO MAKE IT MORE COMPLICATED AND HAIL MARYING THROUGH INDEX EXTRAVAGANZA INSTEAD OF ACTUALLY THINKING ABOUT THE CENTRAL PROBLEM BECAUSE I’M IN A RUSH. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT. THINK BEFORE YOU ACT.

I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I give up. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I am a failure. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right. I can’t do anything right.

D

 

BREAST. BREAST. BREAST. BREAST. So there was that mistress. Her forehead scar, Yellow mind scar. Perky pearly nipples. Baseballs, baseballs. I’ve pinched the life out of those sweet twin tipped tits. I’ve pecked the right with my femlips and narrow insuck whistled Revolutionary tunes on the left. Hah! But it makes me wanna puke, yo. The whole matter was a shield against public attack, anywho. It missed volume. No; it was perfect, but you’ve spoiled me! You’ve warped my mind into darker figures, standing on the wayside of darkly lit streets. Have I found the Yellow Sign? You are my queen, J. You–extravaganza fete fetishist, extravagant spender-eater; pressing your fat tits against those of some Hussar booted braggadician, sharing each others’ healthy meaty flabbiness in warm joy. And I’m here, what? Thinning behind a redoubt on bread? Screwing sticks? Conquering the East as you gain independence at home? Supplant me, for the love of God. Let’s abandon Syria and beyond and I’ll come right on home. Call me home and I’ll be at the behest of your feet. I’ll hang onto your leg like a horny hog OH GOD YES I would climb up, scratching your thighs and belly to reach up and get a taste of your warm breasts. Ah, if I had them before me here right now, I would snort in your dark nipples like a pig. God, your body is so fair, but your nipples are unusually dark, like dirty mounds of peat. They are in my mind as I walk back across the bright, blurry Sinai, keeping me sane. Would I die in a duel for those those dual bowls of faith and justice. MILK AND CURD! I’D TAKE EM BOTH AND YOUD CRY AND I’D LAUGH. YUM YUM YUM YUM YUM. I’m starving. Look at me. Look at how pathetic I am. Take pity on this poor soul. Carry me like a babe and let me bite on the summit of your left mountain. Part D follows immediately from Part C.