2.10: High School Algebra

 

Here's a "basic" one. High school sucked for everyone, so let's get this over with quickly. Yes, our guy is denoting ℝ the real numbers, and ℂ the complex numbers. We're going to compute the spectrum of real polynomials ℝ[x].

Note that ℝ[x] is a PID, hence it is also a UFD, and these two facts combined mean that we're in the lovely "I'm looking for prime ELEMENTS" and prime ⇔ irreducible case.

Q: If you have a real polynomial in a single variable, (e.g. x⁴ + 3x² + 1 or something), what does its factorization look like in general?

A: It factors into linear factors and irreducible quadratic factors.

So those are our primes. Basically, we have all of these guys: x - 0,x - 1,x - ,x - 2,x - 2.5,x - 3,x - π, etc. So basically, I can identify these linear polynomials with the real numbers in ℝ.

And then we have a bunch of irreducible quadratics, e.g. the most famous one x² + 1, which correspond to complex numbers in ℂ. E.g. x² + 1 corresponds to i,-i. In fact, you might remember that when you factor real polynomials, the complex factors always come in conjugate pairs. So if 3 + i is a factor, so is 3 -i.

So here's my drawing of Specℝ[x]:



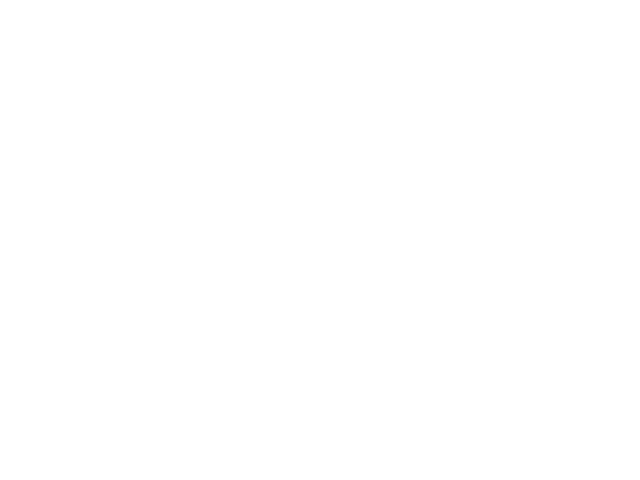
Very simple. It's just the usual complex plane except that I glued the negative imaginary axis with the positive imaginary axis since the conjugates come in pairs. And there's the generic point (0) sending its webs out everywhere. NOTE: Do not get (0) confused with the origin, which is x - 0. Abuse of notation.

Also, since (0) is a generic point for the whole space, by an analagous argument as we performed for SpecZ, the structure sheaf just produces classic rational functions that are nonzero on the given open set.

2.13: Noetherian stuff

 

After varieties, it's tempting to assume spectra are quasi-compact and Notherian and stuff when they might not be, so here are some conditions where we get such "nice" spectra.

A

We'll start with the "only if":

Suppose X is Noetherian. Let U ⊂ X be open, and take

 
to be an open cover of U, weeding out any extraneous sets in this collection (if U_i can be covered by a buncha U_j's in the collection, get rid of the U_i). After the weeding out, if we get a finite open cover, great. Otherwise, take be a countably infinite subset of the cover and order it in a random fashion, yielding a sequence U₁,U₂,U₃,…. I'm gonna define

 
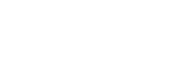In that case,

 
is a descending chain of closed sets of X (properness following from our "weeding out"), but this contradicts Noetherianness of X. So we're done.

⇐=

Now we suppose every open set is quasi-compact. Let

C1 ⊃ C2 ⊃ C3 ⊃

 
be a descending chain in X. Then, taking complements

X - C1 ⊂ X - C2 ⊂ X - C3 ⊂

 
Then

 
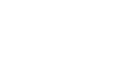is an open set, and thus has a finite cover, which means that the chain terminates.

B

 
Give an open cover of X:

 
where U_αi = X - V (α_i). So

X	= X -⋂ i∈IV (αi)
∅	= ⋂ i∈IV (αi)
∅	= V (∑ i∈Iαi)
V (1)	= V (∑ i∈Iαi)

 
which implies, reordering indices for convenience, there are f₁…,f_n in α₁,…,α_n repectively, such that

 
where no prime ideal P contains ϵ. So we can replace the infinite sum with a finite sum:

 
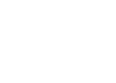and unwrapping and complementing gives us our finite open subcover.

Also, an example of a nonNoetherian spectrum is... let's see...... the infinite variable polynomial ring looks like it works.

C

So we want to show that if A is Noetherian, then so is SpecA. This is easy. Let

V (α1) ⊃ V (α2) ⊃ V (α3) ⊃

 
be a descending chain, which means that

⊂ ⊂ ⊂

 
which terminates because A is Noetherian. And since V ( ) = V (α) , we're done.

D

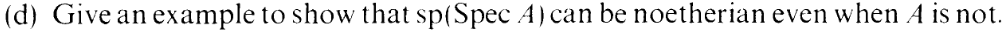
See here (+1).

2.14

 

For context: ProjS:


Which is indeed a scheme by prop 2.5

A

if

We suppose every element of S₊ is nilpotent. In that case, let P be a (homogenous) prime ideal. 0 ∈ P, of course. And given any a ∈ S₊, there is n > 1 where aⁿ = 0, so a ∈ P. But since a ∈ S₊ was arbitrary, S₊ ⊂ P, which means that P ProjS by the definition of Proj. And since P was arbitrary, ProjS = ∅.

only if

Again, we want to prove that:

 
Let s ∈ S₊. Okay. There is a wonderful little construction called the nildradical. It's the radical of (0), i.e., just all the nilpotent elements smashed together into a set:

 
(it's a proper ideal, cause otherwise we'd have 1 = 0)
Now, if this ideal were prime, we'd be done. Because thanks to ProjS = ∅, we'd know that ⊃ S₊, which is exactly what we're looking for. However, that isn't guaranteed.





I've been in a terrible mood–dizzy and tired all day, no matter how healthy I eat, or how much coffee I drink, or how much I sleep. I feel dizzy, useless, migrained. Is it depression? Nope. Its seasickness. No wonder the coffee isn't working. Seasick-on-land, itchy on the arms, always feeling out-of-place, underneath my comrades, homesick for a home warped out of its homely state–stuff my nose against fleshrot. At my desk with logistics for two days and two nights under a sack sanctioned and brushed under the rug by none other than myself, and as my spirits' stomachs and sanity and numbers and spirits wane, the further the inevitable return journey will be. And yet you press on, while self-preserving, just in case. Screams of women, God, someone shut the door. This isn't Romantic at all. What if it's time to turn back? How quickly can you get over your mistakes? WHACK. What is the relationship between means and ends? Are you able to see two days and two nights of failure as a mere blip in the grand scheme of things? In the first minute, two boys both lament the lack of prime-ness. Mal de debarquement. They start on the same square. But as the hours tick, and the sky reddens, one feels the impression of time more deeply than the other. Their paths begin to veer off. They both think, this is ridiculous, but one resolves to do the right thing, with meticulous localizations and numbers, while the other begins to realize that he can get there faster if a plays a darker game, and starts drinking more coffee, sees the seas in land–that type to not turn his head away from constructing pyramids made out of decapitated heads–pyramids made out of lies–and latches onto that terrible idea of something that can't be constructed. Not even in the mind. You think innocently first, and then, pathologically. I'm soulless at present. I need a few days to recover my soul. Ahhh, someone give me a hand, or I'll have to do it myself. Who makes themselves felt on the President's desk on the morning-of? How do you lie in your letter to snipe the rest?

B

Natural map

Let's not put the cart before the horse: Let's assume U is open now (why would we want that to be open anyway?). Denote X = ProjT and Y = ProjS. Let's define:

f : U	→ ProjS
P	ϕ-1(P)

 
Since the inverse image of prime ideals are prime. But hold on. Q = ϕ^-1(P) may not be a valid member of ProjS, if Q ⊃ S₊. Now that's why we defined U. Note:

ϕ-1(P) ⊃ S +
ϕ(ϕ-1(P)) ⊃ ϕ(S +)
P ⊃ ϕ(S+)	cheatsheet
P U

 
which is the contradiction. So ϕ^-1(P) ∈ ProjS as needed.

Now to define the associated sheaf map. Given V open in Y , we want

 
In which case, we can take a natural restriction of a map

 
NATURAL: Compose with the induced maps of stalks ϕ_P.

U is open

Reconsider:

 
This would be immediate if ϕ(S₊) were an ideal, but that isn't necessarily the case. So we'll try and force our way in: Let's consider the smallest ideal containing it. My argument is that I can replace ϕ(S₊) with the ideal I = (ϕ(S₊)) generated by it. Now, P ⊋ ϕ(S₊) P ⊋ I, trivially, so I want to show the reverse of this statement. Let's suppose P ⊋ I. Then there is some f ∈ I such that f P. We can assume wlg that f is homogenous (if f = f₀ + + f_n, then if f_i ∈ P for each i, then f ∈ P). Then by definition of I, I can write f = x ⋅ ϕ(g). If ϕ(g) ∈ P, then x ⋅ ϕ(g) ∈ P i.e. f ∈ P, a contradiction. So ϕ(g) ∈ ϕ(S₊), but ϕ(g) P. So P ⊋ ϕ(S₊).

More next weekend.