II.2.6,8,9
2/4/2022
If you make war, wage it with energy and severity; it is the
only means of making it shorter and consequently less deplorable for mankind.

Ces matins gris si doux...
The Senate recognizes a quorum.
The clerk will read file item 1.
File item 1: Senate resolution 43: In which a floor session in this House is
permitted to coalesce separate topics into one post [in the interest of
maintaining a custom of holding regular sessions once a week, on Fridays].
Gahahahahahahahahahahahahaha! Now that is a joke! Many jokes have been
made in the presence of your fellow legislators, and the gallery peering
upon us from above like gargoyles in the night. And what for? Lulz?
Blblblblblblblblblblblblblblblblblblblblblblblblblblblblblblblblblblblbl. Those damn fools
stuck at the Rhine! How long has it been! Blblblblblblblblblblblbblblblblblblblblblb.
Squander your dignity for a little fame; That's the way, baby. I'm loveless and
lidless. I'm dead. I'm dead. I'm dead. Off to the fields, now. Off the post and
off to the fields, I say! Die that way, rather than be abdicated, I say!
Blblblrrolr. We've killed millions. And the failures of our position are
unpatchable. The party is over. The kingdom is no more. We cannot keep going
up. We cannot reach the heavens. We are stuck here, humbled on the
ground. The party is daily life: the meaningless meandering of now; the
trudge of mundane. *Spits*. Or spend it all and lose it all to fulfill history.
Your destiny may be to be ruined. And that is a valid destiny. "Tragedy
excites the soul, lifts the heart, can and ought to create heroes." A fall
from grace is never graceful; but let it be painted as such, in respectful
memory of the rise. GIVE THE MAN HIS DESSERTS. HIS CAKE, HIS
APPLE PIE, HIS ITALIAN SWEETS. GIVE HIM THE VOLUPTUOUS
BREASTS OF HIS MISTRESS. Big, warm breasts. Big... warm... Ah, procure
me with those pillows. I would become unweaned again to lay on them.
We will adjourn today in memory of The Men Without Fear:
Audible Albert. Boob Bailey. Calculus Cecillia. Dashing Derek. Effeminate
Eunice. Fill-her-up Fuschia. Giga Gordon. Hell Hailey. Irksome Isabelle. Jester
Jelly. KKKMember3. Lapdancing Lanice. Mail-the-goods Melendez. Nifty Nilliam.
OoOoOoO. Pull-me-in Perendez. Questing Quanah. Riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley riley riley riley riley riley riley riley riley
riley riley riley riley riley riley. Stoops-high Sturgeon. Tortoise Timothy.
Umbraged Ursula. Vore-Fetishist Villiam. Whore-Fetishist Wiliam. Xylophone
Xander. Yellow Yonnie. ζ.
2.6: Spec0 is the first scheme

The Senator from SD44 is recognized.
Thank you, President. We shall begin with dual of finality: initiality. Whereas
SpecZ is the final ring, Spec0 is the initial ring. In fact, with 0 itself being a
final ring, it is automatically the initial affine scheme, but we are concerned with
the category of schemes more generally.
The geometry of nothing
The trick is to notice that (0), the only ideal in the ring 0, is NOT prime, as it
comprises the entire ring. Hence,
 |
It as an empty set. We are thus computing the geometry of nothing. The
topology of the empty set is necessarily trivial and the structure sheaf is
necessarily 0:
 |
Paths from the first scheme
Hence, given a scheme X, we'd like to quantify
 |
ϕ is forced to be the vacuous morphism. Given V open in X, we'd like to
quantify
ϕ#(V ) :
 X(V )
X(V ) | →
 Spec0(ϕ-1(V )) Spec0(ϕ-1(V )) |
The right hand side is 0, so this has to be the zero morphism. That finishes 2.6.
2.8: The spectrum of dual numbers

The Senator from SD24 is recognized.
Today, we compute another spectrum. The Spec of the "dual numbers": k[ϵ]∕(ϵ2)
(Sidenote: the Spec of k[ϵ], unquotiented, by the way, looks like this).
Firstly, everything inside k[ϵ]∕(ϵ2) looks like this:
 | (1) |
Call them linear functions, if you'd like.
Now to find its prime ideals. k[ϵ] is a principal ideal ring, so therefore so is
k[ϵ]∕(ϵ2). So every ideal is principal generated by an element in the form of (1).
And what we're really searching for are simply prime elements, up to a constant
factor
*Ahem* It's time, now, that you are introduced to the wonderful world of
nilpotency. When it comes to dual numbers, ϵ2 = 0. Correct: ϵ is a nonzero
number, but when you square it, you get zero. So zero is NOT a prime number in
the dual number system.
Now let's take an element given by (1) more generally. Look what happens when
we multiply by its conjugate:
| (aϵ + b)(aϵ - b) | = a2ϵ2 - b2 | ||
| = -b2 |
So if b≠0, then we are doomed to generate the entire ring (1) = Speck[ϵ]∕(ϵ2),
which doesn't count as prime. Hence, the only option we are left with is for prime
elements are in the form
 |
which all corresponds to the ideal
 |
THAT is our only prime ideal. So the spectrum of the dual numbers is
A SINGLE POINT; Speck[ϵ]∕(ϵ2) = {(ϵ)}, a singleton. However,
EVEN A SINGLE POINT CAN HAVE MANY DIFFERENT
GEOMETRIES ON IT, a la the structure sheaf. Here, we send all sections (of
neighborhoods of y = (ϵ)) to (k[ϵ]∕(ϵ2))(ϵ), and the stalk at y is also the same.
I spy shudders in the audience. Some men following along have encountered a
singleton scheme before. In fact, this ring of dual numbers isn't even the canonical
example of such a case. That would be fields. The men who did encounter it did
so in a 54-minute skirmish on the antepenultimate day of the previous month.
"EVEN A SINGLE POINT CAN HAVE MANY DIFFERENT GEOMETRIES
ON IT, a la the structure sheaf," is, in fact, a quote derived from that very
incident. It was an ugly 54 minutes. 54 minutes of constant flux, where certain
shots and men were fired and withdrawn, fired and withdrawn, as fast as
lightning. Never have I seen a battlefield change so constantly and rapidly in such
a short amount of time. More occurred in those 54 minutes of "skirmish"
than I've seen in some 10 hour battles. Truly, a general can be faulted
but forgiven for attempting to cross the 27th meridian on that day–a
reasonable miscalculation in the number assembled by the enemy–and
he must nevertheless be praised for sucking it up and making the call
to retreat so early. In hindsight, especially, it was a mark of talent to
have recognized the value of that old adage: "Sometimes you have to
lose the battle to win the war." Well, talent, of course, and experience.
And now, the moment you've all been waiting for.


And now, to address the skirmish of yesterweekend:
'Intrigue? Beugh heugh heugh heugh heugh heugh. What do you mean "intrigue"? That man? Intrigue? You're scared of
intrigue from a man of that.... stature? Beugh heugh heugh heugh heugh heugh
heugh heugh heugh. Now THAT'S a joke. Hey, hey, lay another one on me. What
next? Some sort of anti-royalist coup? From that
soldier of the 27th Regiment? Bring it on, I say. BEUGH HEUGH HEUGH
HEUGH HEUGH HEUGH HEUGH HEUGH HEUGH HEUGH HEUGH
HEUGH HEUGH HEUGH HEUGH HEUGH HEUGH'
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Now, referring Y = Speck[ϵ]∕(ϵ2), hence, when we consider a morphism
 |
ϕ selects an element x ∈ X, and given V open in X that is a neighborhood of
x, ϕ# takes the form
ϕ#(V ) :
 X(V )
X(V ) | → (k[ϵ]∕(ϵ2)) (ϵ) | (2) |
(if not a neighborhood of x, the map is trivial, ala the definition of (pre)sheaves).
Now if we localize at x (i.e. drop down to stalks), the induced map is
ϕx# :
 x,X
x,X | → (k[ϵ]∕(ϵ2)) (ϵ) | (3) |
We can hence determine (2) by simply dropping down (3). So (3) is the map that
truly determines ϕ#.
By the way, we should probably figure out what elements of (k[ϵ]∕(ϵ2))(ϵ) look
like. Well, localization means they look like rational (1)s, except we can't divide
by anything in (ϵ). So they look like this:
 | (4) |
Since these are local rings, the maximal ideals of each are unique. The latter's
maximal ideal is the ideal generated by ϵ, which I'll again just denote as (ϵ). And
since this is a local morphism, I know that ϕx#-1((ϵ)) = 𝔪x. Now let me take
quotients and induce the following morphism:
π :
 x,X∕𝔪x x,X∕𝔪x | → ((k[ϵ]∕(ϵ2)) (ϵ))∕(ϵ) | (5) |
STEADY: The enemy is weaker than he appears. The left hand side is just what
we call "k(x)" (notation taken from 2.7). And yes, yes, I understand. The right
hand-side looks intimidating. Stay cool. Do not fear the beast. All we're doing is
taking all the elements in (4) and setting ϵ = 0. So all that we're left with then is
elements of the form
 | (6) |
What did I tell you? Do not fear the beast. That awful thing on the right hand
side of (5) is, in fact, just k. So (5) is just
| π : k(x) → k |
Easy peasy. Now thanks to the stipulation that this morphism is k-linear, this
morphism is surjective. But it is also injective. So it's indeed an isomorphism,
which means that k(x) ≃ k (i.e. "x is rational over k", as Hartshorne puts it).
Finally, (3) can be likened to an element of Tx because everything in 𝔪x gets
mapped to factors of ϵ and the rest gets mapped onto k.
2.9: Generic points
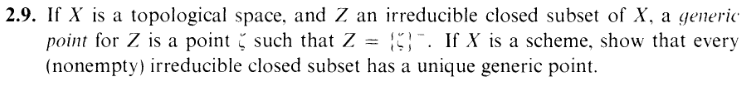
The Senator from SD28 is recognized.

Ks ks. Zip zip zip. Listen: How does one be a generic point? What if you were one
of those imperial generic points? Fashion yourself in red pajamas, laying in
your rickety cot in the corner of your tiny room. You are, truly, just a
weightless point–less than a dot without area or volume–and yet you lay on a
web-blanket–your de facto throne from which you command the entire house, your
webs spread everywhere. You lean to the right and whisper into that fossillike ear
of your aide-de-camp: Reign this one in and tell him to await my next order.
Where is she? You are red and yellow. A click clack in and pssshhhh of water in
the kitchen and some rude thumps. Up the stairs, up the stairs, leg lift and
strumming your strings and humming up. Your webs have been set all over
the house. You retreat and reapportion men, often with them–restlessly
mobile–from Berscia to Castiglione and Roverbella and east then west
then east then west then east then west of Lake Garda. Today, at the
Palazzo Serbelloni: Tug, tug. Lo! in the orient when the gracious light,
lifts up her burning head. The rising sun is prepubescent, and your silk,
catching the bare foot of that little girl, pulls her in, as she protests like an
animal, pulls her in and traps her in your web-bed. Seduced into your
cunny cocoon, her little body is yours to be taken unto with Josephine's
zigzags. ζ. Seize the sweet
morning first, then the day. Ces matins gris si doux? His red torso is
splayed with muntin-divided yellow pieces. A sunny crucifixion. Royal in
the Republic with optics and bluff. Understood? All you are is a point.
You're a snubbable point. A single man in Milan, with understaffed webs
spread but sparsely: checking the Austrian armies to the north, protecting
your rear, maintaining the siege of Mantua, disciplining the Papal States.
Transparently to anyone privy, as vulnerable as a hanged pigeon to a half-decent
revolt. You are a moth that can be squashed between fingers. And yet,
moths live. At awe and charisma, you are generic to where your web of
influence stretches. At your point d'appui, you are the master of your closure.
For example:
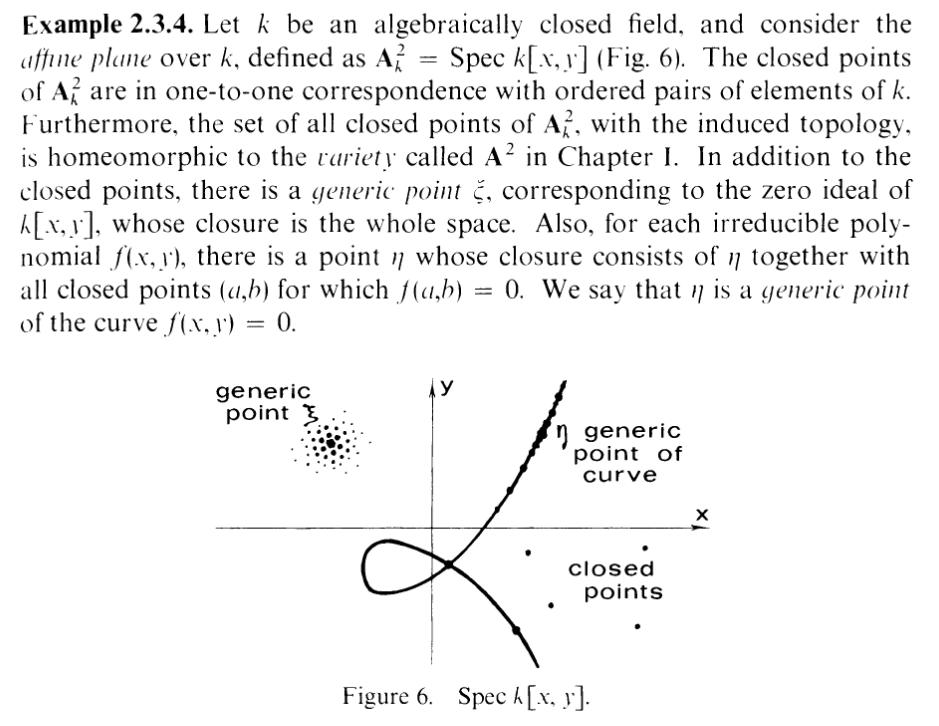
You see what I mean? You are a point that holds an umbrella over many other
points. And in fact, what 2.9 is telling us is that irreducible closed subsets are
ruled by generic points.
Lemma: It holds for affine schemes
Since a scheme is made up of affine schemes, it makes sense to establish the fact
for affine schemes first. Let's suppose X = SpecA, and Z ⊂ X is an irreducible
closed set. I know that
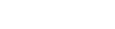 | (7) |
For an ideal of A that I've slyly named ζ. Now note that for an arbitrary prime
ideal P,
| {P}- | = ⋂ V (β)∋PV (β) | "definition" of closure | ||||
| = ⋂ β⊂PV (β) | ||||||
| = V (P) | since V (P) is the "smallest" of these |
In an affine scheme, the closure of a point is its zero set. which means
that if ζ is a prime ideal, I can rewrite (7) as
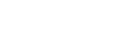 |
and we'd be done. Hence, our goal is to show that ζ is prime.
Let's suppose f ⋅ g ∈ ζ. This implies that V (f ⋅ g) ⊃ V (ζ). And from basic
properties
| V (f ⋅ g) | = V (f) ∪ V (g) | ||
so V (f) ∪ V (g) ⊃ V (ζ). Since Z = V (ζ) is meant to be closed, we have
either that V (f) ⊃ V (ζ) or V (g) ⊃ V (ζ). But this means that f ∈ ζ or
g ∈ ζ. So ζ is prime.
It's also uniquely determined, because if V (ζ) = V (β), with ζ,β prime, then
by definition of V (⋅), we'd have α ⊂ β and β ⊂ α, hence α = β.
It holds for general schemes
Let X now be a general scheme, and Z ⊂ X be irreducible closed. Let U be an
open affine of X that has a nonempty intersection with Z.
Hearkening back to the very early days of Hartshorned, I know that U ∩Z is an
irreducible closed subset of U. Hence, by our lemma , I know that it has a generic
point ζ. Now, ζ is a generic point of U ∩ Z from the perspective of the affine
U. But is it also a generic point of Z from the perspective of X? Well,
| clU(ζ) | = U ∩ Z | (8) |
 clX(ζ) ∩ U clX(ζ) ∩ U | = U ∩ Z | (9) |
Now, on the one hand we have clX(ζ) ⊂ Z, since the closure of ζ is the smallest
closed set containing ζ. And furthermore
| clX(ζ) | ⊃ clX(clX(ζ)) | |||||
| ⊃ clX(clX(ζ) ∩ U) | ||||||
| = clX(Z ∩ U) | (9) | |||||
| = Z | Since U is dense in Z, thanks to I.1.6 again |
So Z has a generic point: ζ. It's the same one that U ∩ Z has. And within
U ∩ Z, I know that ζ is uniquely determined. But what if we had another affine
with its own generic point for Z? Let's suppose we had another affine V yielding
the generic point Q:
| clX(ζ) | = clX(Q) = Z | ||
| P ∈ U, | Q ∈ V |
Well, if Q
 U, then U is a neighborhood of ζ where Q
U, then U is a neighborhood of ζ where Q
 U, so ζ
U, so ζ
 clX(Q),
which is clearly false. So Q ∈ U, but since U is affine, Q = ζ. ζ is uniquely
determined.
clX(Q),
which is clearly false. So Q ∈ U, but since U is affine, Q = ζ. ζ is uniquely
determined.
The Senate has adjourned until next Friday.