As Hifu put it in a recent post, there are times where one is compelled to stop bottling it all in and ”be authentic, oOOooO,” but they feel tempted not to so as not to overshare. How, and to what extent, does one reveal themselves to others? To you, Mr. Representative, I’ll be as authentic as ever. See here? My feminine hands are dirty with earth. And here: Stakes high an’ ugly, with unmarked barrels in and about. Cannons spaced in a crude parody of a sophisticated naval gun row, with a wooden sign marking the name of this battery, carved in as jaggedly as the brass label of a third rate is cursive. We are a pseudo deck parked on the coast. A cobblers patch work in an inconsequential little location. A few barely scraped together little constructions, made up of wood and earth, and stolen cast iron. We look absolutely ridiculous. You could hear em laughing from the other side of the Rade. oOOoOo. Humiliated.



Evariste Galois? Never hearda him. Humiliating. My theoretical knowledge is patchy. I’ve gotta get down n dirty with the machinery, ysee. That’s how i got those two fiber babes up so fast. I GET THE JOB DONE. Set the foundation now, worry about the details later. A separable polynomial has a nonzero first derivative. A separable element in an extension is algebraic over a separable minimal polynomial. Separable closure is the extension whose set is the separable elements in the algebraic closure. Those are the dirty details, and that’s all I need. No #deep Frobenius morphism OooOoOOoOooO nonsense. No certainty, no context. Is that such a handicap? What I do need is AMMO. Organization. Ammunition. Resources. Bread. Stuff. Here I am, with the most down-to-earth plea: ooOOoOOooOOoOOooOOOooOOOooOOOooOOOOooOOOoOOOOoOOoOOoOOOO. Help me out there, will ya? Nevertheless I have two batteries up and running. I’m capitalizing on the little i’ve got. Fibers on the run. I’m doing a great job. Nevertheless, I’m quite well-read. You should see some of the leaders here goin ”oOOooOOOoooOOooooOOOoooOoOOOOOOooOOOOo” at basic artillery facts. Perhaps I should be promoted. I know how to lead. Yes, I can make big decisions. I would like some more ammo, though, but that’s okay, hahahaha, but it’s not. I need ammo. If you give me some ammo, surely I can do this. What is missing here, essentially, is a lack of ammo. I do indeed have a plan. In fact, it has been sent to you many times over, and I shall sneakily take credit for inventing it, but I shall be the most vigorous advocate, you see? I know what I am doing. Now, listen, Rep, here’s what I



oooOoOOooOOOOOoooOOOOoooOOOOOoOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooooooooooooOOOOOOOOoOOoOOOOOOOOOOoOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOooooooooooooOOOOOOOOOOOOOOOOOOOOOOoooooooooooooOOOOoOoOOoOoOOOooOoOOOOOOoOOOOOOOOOOOOOOOOoooooooooooooooOOOOOOOOOOOOOOOOOOOOOoooOOOOOOOOOOOOOOOOOOOOOOOOOOOoOoOOOOOOOOOOOOOOOOoooooooOOOOOOOOOOoOOOOOOOOoOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooooooooooooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooooooooooOOOOOOOOOOOOOOoooooOOOOOOOOOOOOOOOOOooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooooooooOOOOOOOOOOOOOOOOOOOoooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOoooooooooooooOOOOOOOOOOOOOOOOoooooOOOoOooOOoOOOOOoooOOOOOOOOooooooooooooooOOoOoOOOOOooooOOOooOooOOooOOOoooOOOOoooOOooOOOOoOOOoooooOOOOOOOOOOOOOOOOOOOooooOOOOOOOOoooooOOOOOOOOOOOOoOOOOOOOOOOOOoooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooooooooooooooooooooooooooooooOOOOOOOOOOOOOOOOOOOOOOOOOOooooooooooooooooooooooOOOOOOOOOOOOOOO *The reps run away like pussies from sudden onfire, while the boys laugh in the kicked up cloud of dust* Calm down, calm down, Reppie. They make a good show outta the earth, but they’re too far from the coast. Waters too shallow here, ysee, so theydnt be able to maneuver. There’s no authenticity here. Tis merely the screaming of the artillery into the void. You’ll get used to it. Or we will. Ahhh, the loud voices of gunfire in harmony with the voices in our heads. But man, wed be able to fire back a bit if we had a bit more ammo you know. Well anyway thats why im not too concered about Gribeauval or Galois or Grothendieck or whoever. Because we can shoot. That’s the point. Here I am, bringing dignity and form to this area, transforming this cobbler’s battery into something heroic. We have something to work on. Mr. Representative, are you ready to see the culmination of our efforts over the past two weeks? That’s the thing. Eventually one does tease something out. The path to victory begins with a single step, and thus: LET’S DO THIS, MOTHERFUCKERS.





Ah, looks like my geometers are completely missing every single shot. Shit shit, the Reps can’t see that, or I’ll be executed. LOOK AWAY, REPPY. *Reaches into my pants and vigorously scratches balls-itch* LOOK AWAY, YOU SEE? *I subtly turn the scratching on my testicles turn into sexual motions on my cock–the ghostly limbo of masturbation* AHHH, THE FRIGATES. LOOK THEY’RE GONNA FIRE O NOOOOOOOOOOOOOOOOOOO. *The Rep finally looks away, or runs like a pussy again.* No more (s)extensions. Ahahaha... well, um, 2 weeks may have been wasted on that effort, but you see, we’re uhhh geometers not algebraists? The POINT is, in spite of our lack, I have something concrete, or iron, to point at, unlike my predecessors. Indeed, I have something iron to point, huhuhu.


BATTERY OF THE MOUNTAIN, BREECHLESS BRIGADIERS. Fine, fine, they cant quite aim yet, but at least we’re hitting roundshot out of the park. These indecisive ”leaders” didnt even have a park to work out of, till I arrived. And just like that: Fire. OooOOOOooOOOoO, there she blows, yknow. Errr, those far off beasts aside for the time being, what about these little shoaly pontoons? And, what we need is some retired men to work on the broken ordnances; a walk in the artillery park.


–holeinmyheart has failed the authenticity challenge–

3.17

 

Indeed, this is the easiest exercise in the section so far. It solves itself, mostly. The point is to mainly introduce convenient facts and terminology.

First off, yes, a Noetherian scheme is different than a Noetherian space:



Not too complicated, right? Zariski spaces are Noetherian, and they’ve got what I shall call ”THE ZARISKI PROPERTY”:

We already showed that schemes satisfy the Zariski prop, and according to Harty’s caution, Noetherian schemes have Noetherian spaces. So this exercise is, practically, a study of Noetherian schemes, and just how well-behaved they are.

A

 

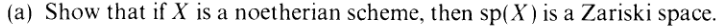
...which I already just casually proved.

B

 

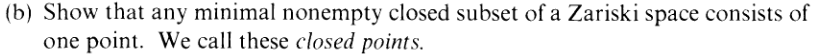
See what I mean by well-behaved? Indeed: The smallest closed sets for a Noetherian scheme are singletons. Let X be a Zariski space, and let C be a minimally closed subset. Now, here’s an old well-established property for us at this point, that I’ll redisplay just for good measure. Irreducible component decomposition of closed sets in Noetherian spaces:




I’m gonna break up our C accordingly:

 


HOWEVER: Any of these irreducible components would be ”more minimal” than C. So we must have that C itself is irreducible (i.e. the decomposition is just trivial: C = C).

Now, since C is irreducible, by the Zariski prop, it’s got a unique generic point, which I’ll call x:

 


We gotta show that it’s a singleton. Suppose we’re given a distinct point P ∈{x}− (if no distinct point exists, we’re automatically done). By the nature of closure, given P ∈{x}− and an open set U:

 


Now, what I’m going to do, oddly, is disprove the converse of it:

(1)

 




Again, I’m going to DISPROVE the above, which is equivalent to the following statement:

 


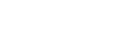But since P ∈ C, we then have {P}− ⊂ C. But by minimality of C, that ”⊂” has to be an ”=”, making P a generic point of C. But by the Zariski property, we’d then have P = x, contradicting distinctness.

Hence, having disproven (1), I can claim there is some open set U where

 


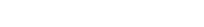Now let D = X − U, to flip that statement:

 


But {P}− is the intersection of all the closed sets that contain P. One of these closed sets is D, but D∌x, which would imply that {P}−∌x. But by minimality of C again, we’re supposed to have {P}− = C. But {P}−∌x would mean C∌x, a blatant contradiction.

So, it’s impossible for that ”distinct” point P to exist. C is a singleton, containing the closed point x.

C

 

SEE what I mean by well-behaved? You might be worried about the topological pathology of non-Noetherian schemes, but do not fret: My proof shall only use the aforementioned Zariski property. that’s right: All schemes are T₀.

Let’s suppose P,Q ∈ X, with P≠Q. Set

C1	= {P}−
C2	= {Q}−

 


C₁,C₂ are irreducible, so by the Zariski prop, their generic points are unique.

Now, note:

P	∈ C2
{P}−	⊂ C 2
i.e. C1	⊂ C2

 


Likewise Q ∈ C₁ implies that C₂ ⊂ C₁. So if we simultaneously had P ∈ C₂ and Q ∈ C₁, then we’d have C₁ = C₂, which would mean P = Q by the Zariski prop. So we’ll assume without loss of generality P C₂. Then U = X − C₂ is an open set containing P but not Q.

(If I did use noetherianness without realizing, let me know).

D

 

Denote ζ the generic point of X. If U is a nonempty open set, then it has a point P ∈ U. But P ∈ X, i.e. P ∈{ζ}−, which means every open neighborhood of P contains ζ, including U.

E

 

Hartshorne says ”generization,” but the more appropriate term for this phenomenon is indeed, generalization. A parabola is a generalization of all the points on it, even while it itself is just a point.

0.0.1 Minimality

So, with this partial ordering, the minimal points–the most specialized points–are closed: The closed points lie at the end of the chain of ⇝s. A closed point is trivially minimal, so suppose x₀ ∈ X is minimal. Let C = {x₀}−. Then

x1	∈ C
x0	⇝ x1
x0	= x1	(by minimality)

 


then we’d have x₀ ⇝ x₁, which implies x₀ = x₁, by minimality. So C is a singleton.

0.0.2 Maximality

The generic point of an irreducible component is clearly maximal, so let’s suppose x_m ∈ X is maximal. Let C = {x_m}−, which is irreducible. If D ⊃ C is an irreducible closed set, then it has a geeric point γ. But

{γ}−	= D
xm	∈{γ}−
γ	⇝ xm
γ	= xm	(by maximality)
C	= D

 


So C is a maximal irreducible closed set, i.e. an irreducible component.

Now let’s suppose C is an irreducible component, with generic point x_m, so {x_m}− = C. I’d like to show that x_m is maximal.

γ	⇝ xm
xm	∈{γ}−
{xm}−	⊂{γ}−
{xm}−	= {γ}−	(Maximality of component C = {x m}−)
xm	= γ	(Zariski property, finally)

 

0.0.3 Stability

Now, in the proofs above, it was perhaps a bit wishy-washy how much Zariskiness we required. However, Hartshorne has dropped the ball on clarity here. It seems like the stability statements apply to only Zariski spaces, but as you shall see I’ll use none of that: The stability statements apply to any topological space.

0.0.4 Under specialization

Let C be closed, x ∈ C. Then {x}− ⊂ C, so C contains all of x’s specializations.

0.0.5 Under generalization

Let U be open, x ∈ U. If y ⇝ x, then x ∈{y}−, and by the definition of closure U ∋ y. Hence U contains all of x’s generalizations.

F

 

Press F to pay respects.