I.7.1
9/16/2021
Welcome to the new section, reader! Spread your arms! Let's do math! First off,
here's a spam of definitions n stuff:
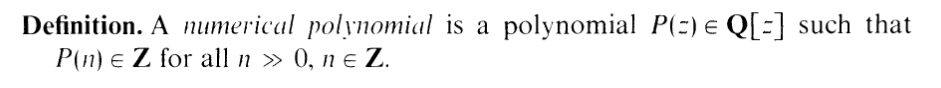

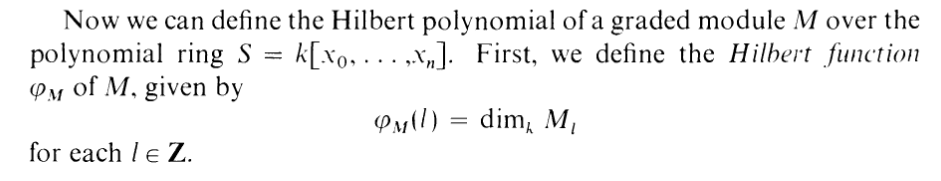



whew. Yea, I actually read most of that, including the proofs (..most of it.).
ANYWAY... part A wants us to calculate the degree of the d-uple embedding
from 2.12 (holy shit that exercise was a lot of work lol).
ALSO: Hartshorne is generous enough to give us the answer: dn. So our job is to
prove it.
Here's an interesting thing tho: degree is NOT preserved over isomorphism. If you
look at Prop 7.6(c) above, you'll see that deg Pn = 1. But Pn is isomorphic to
its d-uple embedding in PN (2.12c), YET, the degree of the embedding is
certainly not 1. Kinda weird to talk about stuff that isn't isomorphism
independent, tbh, but w.e. i guess well roll w it.
OK: so let's bring back some of the notation from 2.12. The d-uple
embedding of Pn into PN is given by Z(α), where α = ker θ, and
θ : k[y0,…,yN] → k[x0,…,xn] sends the yis to d-degree monomials over
x0,…,xn. Hence, to calculate the degree of Y = Z(α), we want to calculate the
Hilbert polynomial of S(Y ) = k[y0,…,yN]∕α, and multiply the leading
coefficient by n! (the d-uple embedding of Pn is isomorphic to Pn, hence the
dimension is n)...... except we don't. Not quite. ysee, I struggled my balls off
trying to calculate the Hilbert polynomial of S(Y ) as given above.... and so I
looked at the solution. SORRY. Here's the trick: use the isomorphism theorem,
and realize that S(Y ) ≃ imθ.... Yea... it's WAY easier to analyze the image of θ
in k[x0,…,xn], lol. Use the image, not the quotient. Got it. let's do that.
BTW: I'm inherting the grading of M = imθ via the isomorphism. So M1 is all
the d-degree elements in k[x0,…,xn], M2 are all the 2d-degree elements, etc.
Then, obviously, Ml is generated by the l-degree monomials over the
indeterminates x0,…,xn. So we need to COUNT (up to constant multiple). Get
in here combinatorics fellas. How many ld degree monomials can you make out of
n + 1 indeterminates. FOLKS: from x0,…,xn, you need to pick ld of them.
Order doesn't matter, and you can reuse elements. So it must be.... a
COMBINATION WITH REPLACEMENT. I.e. the one I have to look up the
formula for. HENCE, we can write the Hilbert function (polynomial) as
| ϕ(l) | =
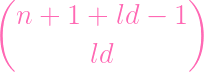 | ||
=
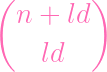 | |||
=
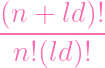 | |||
=
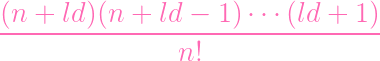 | |||
As per the definition of degree, let's multiply by n!, yielding just the
numerator
(n + ld)(n + ld - 1)
 (ld + 1) (ld + 1) |
Of course, we care about the leading coefficient of this term (seen as
a polynomial over l). And would you look at that? There's exactly n
terms here, so the leading term is dnln, and the leading coefficient is dn.
DONE. NOTE THAT n here is NOT the dimension of the ambient space of
the embedding. That is N. n is the dimension of the preimage of the
embedding. ← i know this is bad gibberish but it makes sense to me lol
B
Okay, same deal, except this time we care about the thing from 2.14:
| θ : k[{zij] | → k[x0,…,xr,y0,…,ys] | ||
| zij |
 xiyj xiyj |
OK: Same trick as last time (USE THE IMAGE, NOT THE QUOTIENT).
Let's look at M = imθ instead of the quotient. GOT IT? Alright. And this
time the grading is: M1 is generated by the 2-degree monomials equally
split between x, y. M2 is generated by the 4-degree monomials equally
split between x, y. Etc. COUNTING TIME AGAIN. To count all the
monomials (up to constant multiple) in Ml, we're combining l elements from
x0,…,xr (with replacement), then combining l elements from y0,…,xs
(with replacement). To pick the xs, we use the same formula from part A:
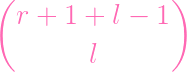 | =
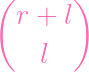 |
Similarly, to pick the ys, it's
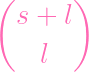 |
So, using the rule of product (BY THE WAY: IF YOU'VE EVER
STRUGGLED WITH COMBINATORICS, STUDY THE RULE OF
PRODUCT (AND THE RULE OF SUM). I SUCKED COMPLETE
BALLS AT COMBINATORICS FOR YEARS AND... WELL, I STILL
SUCK, BUT ONCE I UNDERSTOOD THAT EVERYTHING YOU
DO IN COMBINATORICS BASICALLY COMES FROM THESE
TWO RULES, I FINALLY STARTED TO GET IT) the total number of
ways to pick the l xs, then the l ys is
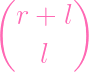
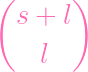 |
(since order doesn't matter, this already covers the case of picking them in the
reverse direction). Okay, phew, now Imma just go ahead and multiply by the
(r + s)! and unwrap this baby (yes i'm assuming the dimension is r + s F U)
(r + s)!

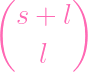 | = (r + s)!
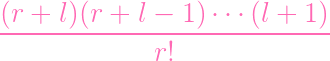 ⋅ ⋅
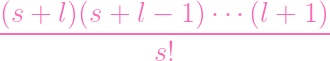 |
OK: So, remember, we only care about the leading term (polynomial over l).
The leading term in the numerator of the first fraction is lr, and the leading term
in the numerator of the second fraction is ls. Hence, in total, the leading term is
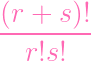 lr+s lr+s |
And that first term is indeed just
 =
=
 , which matches our Queen's
answer, and we are DUN.
, which matches our Queen's
answer, and we are DUN.