I.2.12abc
2/23/2021

Yes, we're doing 3 parts in one post. Strap in.
Half of the challenge is figuring out what the flying fuck is going on, and one thing we've learned in this blog is that
notation is one way to help with that.
Some lemmas, to help me out:
LEMMA 1:
If g is a degree r monomial in k[y0,…,yN], then θ(g) is a degree r ⋅ d monomial in k[x0,…,xn]
COROLLARY:
If g is a degree r homogenous polynomial in k[y0,…,yN], then θ(g) is either a degree r ⋅ d homogenous
polynomial in k[x0,…,xn], or 0
Alrighty. Let's begin.
PART (a):
So I want to show that α is homogenous, eh? First instinct is to find a finite set of homogenous generators for α,
but that isn't a great idea because it's hard, especially so early in the exercise where you're not sure what's going
on. Easier: Let's just show that α is generated by its homogenous elements (i.e. instead of a finite set of homogenous
generators, take all the homogenous elements as a generating set). Indeed, given some f ∈ α, let's decompose f
into homogenous components:
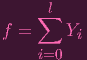 | (1) |
where deg Y i = i
And all we have to do is show that each of these homogenous components are in α in the first place.
Taking θ of both sides, we get
| θ(f) | = θ(∑ i=0lY i) | |||||
 0 0 | = θ(∑ i=0lY i) | (since f ∈ ker θ) | ||||
 0 0 | = ∑ i=0lθ(Y i) |
Now note that we've split θ(f) into homogenous components, with some components possibly being 0: Indeed, by the COROLLARY, each θ(Y i) is either 0 or has degree i ⋅ d. BUT it can't be the latter because then θ(f) would be nonzero (because it'd have nonzero homogenous components). So Y i ∈ ker θ for each i. Thus, α is homogenous.
And how about showing it's prime? Another lesson we've learned through this blog is that it's often easier to use the "QUOTIENT INTEGRAL DOMAIN" thingy instead of showing primeness directly. Now, I did not construct a finite set of generators so I can't do the usual Euclidean division trick like in 1.2 etc. But it's still very easy. What is the IMAGE of θ? Well, it's a subring of k[x0,…,xn]. And subrings of integral domains are themselves integral domains (see e.g. here). So we're DONE. (actually, I now just realized that I could have used this "subring" argument numerous times in the past and skipped a bunch of extra work. WOOPS)
PART (b):
I'll repaste the exercise here for reference!

One inclusion is, in fact, easier than the other. It's the imρ
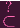 Z(α) one.
Z(α) one.Give me an element P ∈ Pn and pick an affine representative a = (a0,…,an) for it (BTW, if you're confused about the phrasing of the exercise where it says "M0(a)" etc., that's what they mean).
Now give me an element f ∈ α, and break up f into monomials:
| f | = ∑ iY i |
Write Y i = ciy0bi,0y 1bi,1
 y
Nbi,N. And note that θ(Y
i) = ciM0bi,0M
1bi,1
y
Nbi,N. And note that θ(Y
i) = ciM0bi,0M
1bi,1
 M
Nbi,N So we can then
write
M
Nbi,N So we can then
write| f | = ∑
iciy0bi,0y
1bi,1
 y
Nbi,N y
Nbi,N | |||||
 θ(f) θ(f) | = ∑ iθ(Y i) | |||||
 0 0 | = ∑ iθ(Y i) | (f ∈ ker θ) | ||||
 0 0 | = ∑
iciM0bi,0M
1bi,1
 M
Nbi,N M
Nbi,N | |||||
 0 0 | = ∑
iciM0(a)bi,0M
1(a)bi,1
 M
N(a)bi,N M
N(a)bi,N | (plugging in a) |
But the right hand side is just the point ρ(P) plugged into f, so f(ρ(P)) = 0. Since f ∈ α was arbitrary, ρ(P) ∈ Z(α). And since P was arbitrary, imρ ⊂ Z(α) indeed.
Yeah.... "easy". Now you want to see "hard" (aka "some calculation")? Get fucking ready.
To make everything easier to see, I'm actually going to work for the specific case where n = 2 and d = 3. DON'T WORRY. It does generalize, and the generalization is straightforward (except for one part, as you'll see, lol). We've been ignoring the actual format of the monomials Mi up to now. What I'm going to do is actually show you what they look like. For instance, we know that θ maps y0 to some d-degree monomial in k[x0,…,xn]. Which one? Well, that depends on how you order the monomials. I'll order them like this, without loss of generality:
| y0 |
 x03 x03 | ||
| y1 |
 x02x1 x02x1 | ||
| y2 |
 x02x2 x02x2 | ||
| y3 |
 x13 x13 | ||
| y4 |
 x23 x23 | ||
| y5 |
 x0x12 x0x12 | ||
| y6 |
 x0x22 x0x22 | ||
| y7 |
 x12x2 x12x2 | ||
| y8 |
 x22x1 x22x1 | ||
| y9 |
 x0x1x2 x0x1x2 |
"WTF is with that unnatural ordering". Trust me, reader. It'll help. Yes, in the more general case, I'm putting the x0d term in front, and then setting yi = x0d-1xi all the way up to i = n.
If you give me a point c = (Y 0,…,Y N) ∈ Z(α), what do I want? I want c to be in the image of ρ. I want (Y 0,…,Y N) = (M0(a),…,MN(a)) for some a = (X0,…,Xn) ∈ Pn. I.E. I want a solution to the following system of equations:
| Y 0 | = X03 | ||
| Y 1 | = X02X1 | ||
| Y 2 | = X02X2 | ||
| Y 3 | = X13 | ||
| Y 4 | = X23 | ||
| Y 5 | = X0X12 | ||
| Y 6 | = X0X22 | ||
| Y 7 | = X12X2 | ||
| Y 8 | = X22X1 | ||
| Y 9 | = X0X1X2 |
(the Y is are the "given" scalars, and the Xis are the "unknowns") Erm...well that's a complicated system of equations. It's not even linear (...okay, now I'm actually starting to miss linear algebra). What do?
It's pretty easy to show that at least one of Y 0,Y 3,Y 4 must be nonzero (EXERCISE LEFT TO READER LOL). Well, you've already pointed out my funny ordering of the monomials: Yes, I'm assuming without loss of generality that Y 0≠0. Now take a look at that first equation: Y 0 - X03 = 0. Since we're in an algebraically closed field , we can actually narrow down the possible solutions of X0 to a set of at most three elements. Let's call them X0′,X0′′,X0′′′. I know that X0 ∈{X0′,X0′′,X0′′′}. Okay. Cool. Which one?
This is where I got stuck for a considerable amount of time, playing with the other equations and trying to eliminate some of the options... It didn't turn out well. In fact, it turned out so badly that I got angry and decided, "FUCK IT. LET ME JUST PICK ANY ONE OF THEM AND SEE WHAT HAPPENS."
YES. LET'S JUST SET X0 = X0′ AND SEE WHAT GOES WRONG. Well, here's something interesting: once I've arbitrarily set X0 in that manner, that FULLY DETERMINES the other variables. Look at the next 2 equations (in general, the next n equations). I can divide by X02 on both sides (since it's nonzero, heh) and I get
| X1 | = Y 1∕(X02) | ||
| X2 | = Y 2∕(X02) | ||
So now we have a possible solution for X0,X1,X2. We have something that at least satisfies the first 3 equations (in general, the first n equations). Does it satisfy the rest? Well, let's try the 4th equation: Y 3
 X
13. Suppose
equality didn't hold. Then we'd have:
X
13. Suppose
equality didn't hold. Then we'd have: | Y 3 | ≠X13 | ||
 Y 3 Y 3 | ≠(Y 1∕(X02))3 | ||
 Y 3X06 Y 3X06 | ≠Y 13 | ||
 Y 3Y 02 Y 3Y 02 | ≠Y 13 | ||
 Y 3Y 02 - Y 13 Y 3Y 02 - Y 13 | ≠0 |
What I'm saying is that the point c = (Y 0,Y 1,Y 2) is not zero at the polynomial g = y3y02 -y13 ∈ k[y0,…,yN]. However, what happens when we map this under θ?
| y3y02 - y13 |
 (x1)3(x03)2 - (x02x1)3 (x1)3(x03)2 - (x02x1)3 | ||
| = x13x06 - x06x13 | |||
| = 0 |
Yep, g ∈ ker θ. And we assumed that c ∈ Z(ker θ) in the first place, so that would be a contradiction. So our (X0,X1,X2) has to satisfy that 4th equation.
.....Now we just have to verify it satisfies the other 5 equations. Fuck. That's a lot of work. And this is just the case of d = 3,n = 2. What if we had like, d = 100,n = 1000? This is one place where I guess I need to take a detour from the specific case and show it works for the more general case...
Okay, so in the more general case, what's going on?
The relationships given by θ are
| y0 |
 x0d x0d | ||
| y1 |
 x0d-1x1 x0d-1x1 | ||
| y2 |
 x0d-1x2 x0d-1x2 | ||
 | |||
| yn |
 x0d-1xn x0d-1xn | ||
 | |||
| yk |
 x0b0x1b1 x0b0x1b1
 xnbn xnbn | ||
 | |||
The last case is the most general case, where the right hand side is an arbitrary d degree polynomial (b0 + b1 +
 + bn = d).
+ bn = d).Given a point c = (Y 0,…,Y N) ∈ Z(α), we need a point a = (X0,…,Xn) ∈ Pn to satisfy
| Y 0 | = X0d | ||
| Y 1 | = X0d-1X1 | ||
| Y 2 | = X0d-1X2 | ||
 | |||
| Y n | = Xnd-1Xn | ||
 | |||
| Y k | = X0b0X1b1
 Xnbn Xnbn | ||
 | |||
Again, picking an arbitrary solution for the first equation, we use the next n equations to set
| X1 | = Y 1∕(X0d-1) | ||
| X2 | = Y 2∕(X0d-1) | ||
 | |||
| Xn | = Y n∕(Xnd-1) | ||
And now we need to show that our choice satisfies the arbitrary equation
| Y k |
 X
0b0X1b1 X
0b0X1b1
 Xnbn Xnbn | ||
So again, we assume for the sake of contradiction that it doesn't, so
| Y k | ≠X0b0X1b1
 Xnbn Xnbn | ||
 Y k Y k | ≠X0b0(
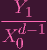 )b1 )b1
 ( (
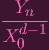 )bn )bn | ||
 Y k Y k | ≠X0b0
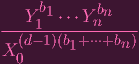 | ||
 Y k Y k | ≠X0b0
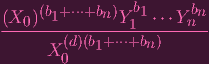 | ||
 Y k Y k | ≠
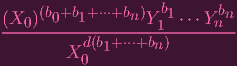 | ||
 Y k Y k | ≠
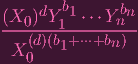 | ||
 Y k(X0d)(b1+ Y k(X0d)(b1+
 +bn) +bn) | ≠(X0)dY 1b1
 Y nbn Y nbn | ||
 Y k(Y 0)(b1+ Y k(Y 0)(b1+
 +bn) +bn) | ≠(Y 0)Y 1b1
 Y nbn Y nbn | ||
 Y k(Y 0)(b1+ Y k(Y 0)(b1+
 +bn) - (Y 0)Y 1b1 +bn) - (Y 0)Y 1b1
 Y nbn Y nbn | ≠ 0 | ||
yes, that was a fucking pain to type out. NOW, following what we were doing earlier, Let's consider the polynomial
| g | = yk(y0)(b1+
 +bn) - (y0)y1b1 +bn) - (y0)y1b1
 ynbn ynbn |
So we're saying that g(c)≠0 Putting this under θ yields
(x0b0x1b1
 xnbn)(x0d)(b1+ xnbn)(x0d)(b1+
 +bn) - (x0d)(x0d-1x1)b1 +bn) - (x0d)(x0d-1x1)b1
 (x0d-1xn)bn (x0d-1xn)bn |
Which is clearly equal to 0, which means that the g ∈ Z(α), which means that we'd need g(c) = 0, a contradiction.
SO THAT'S THE FUCKING GENERAL CASE. *Pant pant* BACK TO d = 3,n = 2.
So, let's review: From Y 0 = X03, we had three choices: X0 ∈{X0′,X0′′,X0′′′}. What did I do? I just daredeviled it and arbitrarily picked one of them. And what was the result? It just werkd. Yes, turns out, we can pick any one of them and that yields a solution.
When you think of the equations
| Y 0 | = X03 | ||
| Y 1 | = X13 | ||
| Y 2 | = X23 | ||
They each yield 3 possibilities
| X0 ∈{X0′,X0′′,X0′′′} | ||
| X1 ∈{X1′,X1′′,X1′′′} | ||
| X2 ∈{X2′,X2′′,X2′′′} | ||
If you pick X0 = X0′, then that forces the choice X1 = X1′,X2 = X2′ (assuming I've ordered them in the right way), so we can set a = (X0′,X1′,X2′). Similarly, picking X0′′ forces a = (X0′′,X1′′,X2′′), and picking X0′′′ forces a = (X0′′′,X1′′′,X2′′′). Any of these 3 choices work (in general, d choices); i.e. any of them map to c under ρ. So we're done.
PART (c):

Alright, to show that it's a homeomorphism, we need to show that ρ is bijective. And that both it and its inverse is continuous.
"Wait... bijective? Didn't you just say there 3 possible points that map to a point in Z(α)? That contradicts injectivity."
.........FUCK. So.... uhh......... did I completely fuck up part (b)?
Okay, are you ready for some high IQ shit. We actually do have some leeway, because we're working in projective space. Indeed: There is a way that (X0′,X1′,X2′), (X0′′,X1′′,X2′′), (X0′′′,X1′′′,X2′′′) can all actually be the same point: If they are scalar multiples of each other.
Well, are they?
Let me start by setting s = X0′∕X0′′, so that X0′ = sX0′′.
Okay, so given that, how does X1′′ relate to X1′? Let's see...
| X1′′ | = Y 1∕(X0′′)2 | ||
| = Y 1∕(sX0′)2 | |||
=
 (Y 1)∕(X0′)2 (Y 1)∕(X0′)2 | |||
=
 X1′ X1′ | |||
FUCK. By an entirely analogous argument, we get X2′′ =
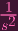 X2′. I wanted X1′′ = sX1′ and X2′′ = sX2′.
But instead of s, we have
X2′. I wanted X1′′ = sX1′ and X2′′ = sX2′.
But instead of s, we have
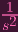 .
.How fucked am I? I am actually not so fucked. You see, s is a very special scalar. Remember: (X0′)3 = Y 0. But also, (X0′′)3 = Y 0. In other words, (X0′)3 = Y 0 and (sX0′)3 = Y 0. I.e. (X0′)3 = (sX0′)3. Isn't that strange? Slightly unintuitive? What's up with this scalar? If I didn't notice this pecularity, I might have thought I did something wrong on part (b). But check this out:
| (X0′)3 | = (sX0′)3 | |||||
 (X0′)3 - (sX0′)3 (X0′)3 - (sX0′)3 | = 0 | |||||
 (X0′)3 - s3(X0′)3 (X0′)3 - s3(X0′)3 | = 0 | |||||
 (X0′)3(1 - s3) (X0′)3(1 - s3) | = 0 | |||||
 (1 - s3) (1 - s3) | = 0 | (since Y 0≠0) | ||||
 s3 s3 | = 1 |
The mysterious scalar s is actually a root of unity! In our case, it's a 3rd root of unity (in the general case, a dth root of unity). In particular, we can divide by 1∕s2 on both sides (more generally, 1∕sd-1) and we get
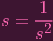 | (2) |
Holy fuck. Hence, we actually do have that X1′′ = sX1′, and X2′′ = sX2′′. and a similar argument for the
triple prime case. So we can in fact write (X1′,X2′,X3′) = (X1′′,X2′′,X3′′) = (X1′′′,X2′′′,X3′′′) since
they only differ by scalars, thus making ρ injective, and making us.... SAFE!

Motherfucker. So bijectivity is done. Now we need to show the continuity requirements
Note that a closed set C of Z(α) can be written as C = Z(β) ∩ Z(α).
Alright. Here we go. We already have a map θ : k[y0,…,yN] → k[x0,…,xn]. And it's pretty easy to see that
ϕ-1(Z(α) ∩ Z(β)) = Z(θ(β)), so ϕ-1 is a closed map (TL note: "pretty easy to see" means "I have
faith").
To show ϕ is closed, I'll do it by way of the d = 3,n = 2 example. Take Z(f1,…,fr) is a closed set in P2. Yes,
we can assume a finite set of generators by Noetherianness, and we can in fact assume they're homogenous. We want
to create another set δ ⊂ k[y0,…,yN]. such that Z(f1,…,fr) is mapped onto Z(δ) ∩ Z(α) Okay. let's look at
f1 for example (just call it f for now). If f has degree that is a multiple of d, then just rewrite f1 in
terms of the yis. E.g. if f = x02x14 - x13x23, then set g = y1y3 - y3y4. and we know a point
that satisfies f has to satisfy g when mapped under ρ, so we can add g to δ. Well... there are other
ways to write g, aren't there? Fuck it, just include every possible way to write g in δ just in case
lol (IMO, it doesn't matter, because we've already included the requirements of α, s we know that
g = y1y3 - y3y4 must "evaluate to" f = x02x14 - x13x23. But no harm in adding the extra gs I
guess).
On the other hand, f's degree may not be a multiple of d. E.g. we may have
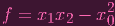 |
In this case, we can "force" it to have a degree of d, by multiplying both sides by e.g. x0:
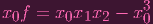 |
allowing us to set a corresponding "g0" accordingly (in our case g0 = y9 - y0). But that choice of x0 is kind of
arbitrary, isn't it? Yes, Because we're only requiring that our point satisfy x0 or f. We included all the points
where x0 = 0! i.e. We included an entire hyperplane. Woops. But no worries, because we can also
include
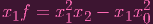 |
and find a corresponding g1 for that. And finally
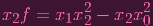 |
and grab a corresponding g2, And we include all the gis in δ. Now a point can't get away with simply being on a
hyperplane, because if it doesn't satisfy f in at least one of the equations, then it would be all 0, which doesn't
count as a point in projective space.
So part (c) is done. That was.... a little hand-wavy admittedly. Oh well. I think it works.
I also wanted to throw in part (d), but I've spent 2 hours typing this out already, so I'm spent for the night. Which
does beg the question of "is it really worth typing all this out if it takes hours to do so", to which I have
to keep reminding myself that the answer is "yes, because publishing this gives me accountability
and is practically the only thing keeping me from falling off track, and also all this work would get
lost in my scrap paper if I don't type it up leaving me with basically no reference when I need to
look back, and typing it up forces me to reinforce the ideas by thinking about how to organize it as
well as forcing me to catch a shitload of errors in my work because, compared to just putting it in a
notebook, I have higher standards when I have to justify my work to you, dear reader *blows kiss*"