Hi. This post will be quick and dry (just like sex with your wife, hahaha). Yes, an extremely scary-looking exercise. But it's actually a very similar process to what I did in 2.12b . In fact, it's even easier.

Letting θ denote the k[{z_ij}] → k[x₀,…,x_r,y₀,…,y_s] map the hint gave us, we set α = ker θ and we wanna show that imϕ = Z(α).

"One inclusion is easier than the other," said 2.12b, and the statement holds analogously here. Give me a point P = (a₀,…,a_r) × (b₀,…,b_s) ∈ P^r × P^s, so that ϕ(P) = (…,a_ib_j,…). Now give me an f(…,z_ij,…) ∈ α.

f(…,zij,…)	∈ ker θ
θ(f(…,zij,…))	= 0
f(…,θ(zij),…)	= 0
f(…,xiyj,…)	= 0
f(…,ai,bj,…)	= 0
f(ϕ(P))	= 0

Since f ∈ α was arbitrary, ϕ(P) ∈ Z(α). And since P was arbitrary, imϕ ⊂ Z(α)

Now for the reverse inclusion. Given C = (…,c_ij,…) ∈ Z(α), can we find P = (a₀,…,a_r) × (b₀,…,b_s) ∈ P^r ×P^s such that ϕ(P) = C

I.e. we need to satisfy (…,a_ib_j,…) = (…,c_ij,…).

I.e. we need to satisfy a_ib_j = c_ij (up to a constant multiple independent of i,j).

So what do we do? Same thing in 2.12b: Line up the requirements, "force" values for our a_i,b_js, verify that they actually work.

First, I'll assume that c₀₀≠0 without loss of generality. Now, let a₀ be.... anything but zero. Yes. You heard me right. Let a₀ be literally fucking anything you want it to be, reader, as long as it's nonzero and from k.

Then check out these requirements:

a0b0	= c00	a0b0	= c00
a0b1	= c01	a1b0	= c10
a0bj	= c0j	aib0	= ci0
a0bs	= c0s	arb0	= cr0

As soon as a₀ is fixed, so is everything else:

b0	= c00∕a0	a0	= c00∕b0
b1	= c01∕a0	a1	= c10∕b0
bj	= c0j∕a0	ai	= ci0∕b0
bs	= c0s∕a0	ar	= cr0∕b0

So choosing anything for a₀ forces all of P. Now we just have to check that ϕ(P) does indeed equal C. I.e. we need to check if a_ib_j = c_ij. Well, based on our settings,

aibj	=
	=

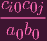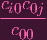Now suppose, for the sake of contradiction, 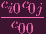did NOT equal c_ij. Then that would mean

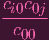	≠cij
ci0c0j	≠cijc00
ci0c0j - cijc00	≠ 0

I.e. we'd have that C does NOT satisfy the polynomial

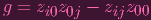But, of course,

θ(g)	= xiy0x0yj - xiyjx0y0
	= 0

So g ∈ ker θ i.e. g ∈ α. By assumption, C ∈ Z(α), yielding a contradiction.

Don't worry. The next exercise is another 3-parter.