I.2.15ab
3/8/2021
q = xy - zw (a) Show that O is equal to the Segre embedding of P1 × P1 in P3 for suitable choice of
coordinates 
Did my little reader miss getting Hartshorned? Did they miss getting licked in the ass by cold crunchy ice? Come
on, now, pull your pants down. Come on pull em down. Oh come on, don't be shy. Pull them down.
Come on babe... PULL EM DOWN, MY TONGUE IS TWITCHING. I'VE HAD NO MATH FOR A
FORTNIGHT, OR RATHER, A WEEK, WHICH IS A FORTNIGHT IN HARTSHORNED YEARS. OR
RATHER, I'VE HAD "MATH" MERELY IN THE FORM OF 12 CASES OF SYSTEMS OF LINEAR
EQUATIONS. "Stop sexually harrassing your readers because you're frustrated at math." I SAID PULL
DOWN YOUR FUCKING PANTS, YOU PRUDE. MY TONGUE IS COLD. I NEED WARMTH.
*PANT PANT PANT* GIVE. ME. YOUR. BUTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT.
This blog, I would say, has been a success. Well I just ruined it with the last paragraph, but it was riding out pretty
well until then. No, no, really. I don't mean to sound egotistical here, but the accountability has done wonders for
my hair. The bags under my eyes have turned pink, and I've moved a couple of hops down the cycloid of ambiguous
progress. Mmmm, you see, it's just that... you know, I'm hitting the cusp. The downward edge of
the cusp. That is to say, I am about to "bounce off", back up, like a phoenix, but you know, I'm a
little before that moment. You have to deal with the periodic dumps. After all, you are you. Yuck.
Listen: You know what I believe? The "procrastination
master" deserves as much credit as the hard worker. What exactly does it take, to master procrastination? To be an expert in failure? One has try and try
again. The undisciplined little one doesn't know when to give up. You have to give some respect to that. Yes, this blog has been a success. Because, as we all know, the purpose of this blog is
not to get better, but to get worse. Let us begin.
...Nevermind. That looks horrifically familiar to one of the polynomials used to generate [CENSORED]. Yeah...
NVM, I'M NOT BACK. LET ME PROCRASTINATE SOME MORE. SEE YOU AGAIN NEXT WEEK.
Well, okay, you know what? It's just one of the polynomials, so it looks like we should be safe. As long as we don't
have to deal with another 2.12d, I'm good. Let's begin.
This... is... The exact same format as 2.12d.
NVM, I'M NOT BACK. LET ME PROCRASTINATE SOME MORE. SEE YOU AGAIN NEXT WEEK.
Okay. Fine.
You want me to prove that? Oh, sure, reader, I can """prove""" it. In fact, I'll go ahead and "prove" it the exact
same way I "proved" I.2.12d. And this time it will look even more airtight and correct.
You see, I.2.14 gave us the definition of the Segre embedding as
| ϕ : P1 × P1 | → P3 | ||
| (a,b) × (c,d) |
 (ac,ad,bc,bd) (ac,ad,bc,bd) |
Hence, to satisfy q = 0, it makes the most sense to label the coordinates w,x,y,z in that order, thus making our coordinate ring k[w,x,y,z]
We want to show that imϕ = Q. Now, of course, 2.14 told us that imϕ could be written as Z(α), where α is the kernel of
| θ : k[w,x,y,z] | → k[r,s,t,u] | ||
| w |
 rt rt | ||
| x |
 ru ru | ||
| y |
 st st | ||
| z |
 su su |
So what we really want to show is that Z(q)
 Z(α). But note that
Z(α). But note that | Z(q) = Z(α) | ||||||
| ⇐⇒ | I(Z(q)) = I(Z(α)) | |||||
| ⇐⇒ | (q) = α | (since q is irreducible and α is prime (the latter of which, it turns out, I forgot to show last time, LOL. You'll just have to trust me, the reliable holeinmyheart admin, on that one)) | ||||
So our problem is equivalent to the problem of showing (q)
 α. Now q ⊂ α is the obvious inclusion, so let's turn
our attention to the reverse inclusioncan .
α. Now q ⊂ α is the obvious inclusion, so let's turn
our attention to the reverse inclusioncan . Give me an f ∈ α. Remember α = ker θ. So by the Euclidean division argument that I've done like 5 times since I've started this blog, I can write
 |
where r ∈ k[x,y,z] and θ(r) = 0.
If we show that r = 0, we're done. Now time to pull out the fuckery that got me in trouble last time.
Using multivariate notation ,
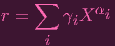 |
where αi = [ai,bi,ci] is the exponent vector for variables x,y,z respectively. And we can assume that we've
collected like terms, so that each αi is distinct
Now,
| 0 | = θ(r) | ||
| = ∑ γiθ(xaiybizci) | |||
| = ∑ γi(ru)ai(st)bi(su)ci) | |||
| = ∑ γiraisbi+citbiuai+ci) |
Hence the exponent vectors for the image can be written as βi = [ai,bi + ci,bi,ai + ci]. Now are all of these vectors distinct? Suppose β1 = β2. Then we'd need
| a0 | = a1 | ||
| b0 + c0 | = b1 + c1 | ||
| b0 | = b1 | ||
| a0 + c0 | = a1 + c1 |
Substituting the first equation into fourth, and the third equation into the second, clearly gives us
| a0 | = a1 | ||
| b0 | = b1 | ||
| c0 | = c1 | ||
| d0 | = d1 | ||
Well, folks. Looks pretty solid, eh? Do you see a #holeinmyreasoning? Because it's apparently this very solid reasoning that led me to fucking proving absurdities about [CENSORED].
Welp, I'M JUST GONNA TAKE IT AND GO. ON TO PART B.
PART (b)

Annnnnnnnd. Here's where the real fun starts, and by "fun" I mean "linear algebra" (so not so fun). No, really, part (b) is the gift that keeps on giving. The funny thing is that...I kinda figured it out like 2 days ago. It's just that, THERE. ARE. SO. MANY. FUCKING. CASES. TO. CHECK. I didn't show you the figure yet, so here it is, now that it's relevant:
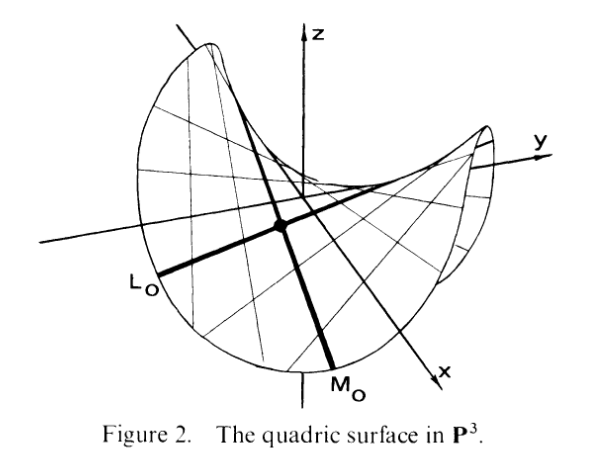
Now, I'll talk some philosophical nonsense about this shortly, but first let's do a little work. Do you remember linear varieties? Give me any line N ⊂ P3. By 2.11b, I know it's minimally generated by 2 polynomials, say, N = Z(f0,f1) where
| f0 | = a0w + b0x + c0y + d0z | ||
| f1 | = a1w + b1x + c1y + d1z |
Hence, if a point P = (A,B,C,D) is in N, it'd have to satisfy
| a0A + b0B + c0C + d0D | = 0 | ||
| a1A + b1B + c1C + d1D | = 0 | ||
![[ ]
a0 b0 c0 d0
a1 b1 c1 d1](Ip2p15ab9x.png) |
Now, what is the rank of this matrix? It's 2. If it was 0, then that'd be fucking retarded (�— brilliant
reasoning). If it was 1, then f0,f1 would be linearly dependent, so we'd just need one of these to
generate the ideal, contradicting the minimality of our generating set. The rank of the matrix is 2, folks.
Hence, we will be able to write the solution set with 2 independent variables and 2 free variables.
For now, let's just say that A,B are the independent variables, and C,D are free. The most general case of this
looks like this:
| A | = lC + mD | ||
| B | = +nC + oD |
Hence, we can parametrize N as
| δ : P1 | → P3 | ||
| (C,D) |
 (lC + mD,nC + oD,C,D) (lC + mD,nC + oD,C,D) |
just as the exerise asks us to.
Also note, given two linear varieties N = Z(f0,f1), M = Z(f2,f3), what happens when we intersect them? Well, we get K = N ∩M = Z(f0,f1,f2,f3). And the dimension of K depends on the rank of the 4x4 matrix given by f0,f1,f2,f3. The rank is at least 2 since, e.g., f0,f2 are independent. So the rank can be 2, 3, or 4. Rank 2 is the N = M case, rank 3 is that N ∩ M = {*} case, rank 4 is the N ∩ M = ∅ case.
Nice, that looks pretty nice. If N≠M are lines, then we get either a singleton or an empty set. I guess we're finished with this exercise?
NOPE.
WE AREN'T DONE FOLKS. NOT EVEN CLOSE.
Now here's the ARMCHAIR PHILOSOPHY SECTION: First note that I only assumed that N ⊂ P3 in this discussion so far. All I've shown is that "lines in P3 either coincide, intersect at exactly one point, or don't interect at all". I haven't even brought Q into the picture. What's so particular about lines in Q vs lines in a mostly standard 3D space P3. It's easy to miss if you don't read the exercise carefully. I almost missed it at least. This exercise is asking us to partition the lines. Since we are supposd to consider lines in Q, which is a 2D space, let's go ahead and picture a standard 2D plane as an analogy (say, the "x-y" plane of ℝ2. In 2D plane, any two lines either coincide, intersect at one point, or don't intersect at all. But, now, how would I partition these lines so that within each collection, intersections give me an empty set but between collections, intersections give me singletons. The best I can do is collect all parallel lines together. In which case... I have infinitely many collections of lines. Now how does this differ from our 2D space Q? In Q, I can partition the lines in a way that I only need two, just TWO collections of lines. With just those two collections, intraintersections are empty sets and interintersections are singletons (yes, I just made up those words. I warned you about the "philosophy").
So, right. We have more work to do.
More.... linear... algebra to do.....
Okay..... Fine. Clearly the point here is to bring back in the surface Q = Z(xy -zw). Basically, now let's assume that N ⊂ Q (not just N ⊂ P3. That point P = (A,B,C,D) we were considering? Now it has to also satisfy BC - AD = 0. I'll actually write AD - BC = 0 cause idk my brain likes it better.
So, with the extra assumption that N ⊂ Q, what happens to our solution set now? Remember, N is represented by a rank 2, 2x4 matrix
![[ ]
* * * *
* * * *](Ip2p15ab11x.png) |
And P = (A,B,C,D) ∈ N iff A,B,C,D satisfies the linear equations given by those coefficients (imagine the
zero vector appended to the end to make an augmented matrix, if you'd like).
Now, folks. I need to classify the solutions, right? Here's what I'm going to do: I'm going to check every single
possible format of an RREF of a 2x4 matrix.
Yes, this is going to be painful. No I do not currently know of a faster way of doing this.
For example, let's start with the easiest case:
CASE 1:
![[ ]
0 0 1 0
0 0 0 1](Ip2p15ab12x.png) |
This is the solution
| C | = 0 | ||
| D | = 0 |
Now, we assumed that N ⊂ Q, so these solutions have to satisfy AD - BC = 0. Do they? Clearly they do, so this is one type of solution that checks out. I'm going to call this solution "TYPE H"
And so on.... Now we check
CASE 2:
![[0 1 a 0]
0 0 0 1](Ip2p15ab13x.png) |
(where a ∈ k is some coefficient). Which corresponds to the solution
| B | = -aC | ||
| D | = 0 |
Now AD - BC = 0 were to hold, we'd get
| AD - BC | = 0 | ||
 A ⋅ 0 - (-aC) ⋅ C A ⋅ 0 - (-aC) ⋅ C | = 0 | ||
 aC2 aC2 | = 0 |
Now, the key point here is that P is an arbitrary point that satisfies f0,f1. C is a free variable. So we can make C be whatever we want in this context. E.g., if I set C = 1, I get
 |
So our original solution can be rewritten as
| B | = 0 | ||
| D | = 0 |
I'll call this solution "TYPE I"
Now let's look at
CASE 3:
![[ ]
1 a b 0
0 0 0 1](Ip2p15ab17x.png) |
which corresponds to
| A | = -aB - bC | ||
| D | = 0 |
Putting this into AD - BC = 0, we have
| AD - BC | = 0 | ||
 A ⋅ 0 - BC A ⋅ 0 - BC | = 0 | ||
 - BC - BC | = 0 | ||
 BC BC | = 0 | ||
Now, REMEMBER: B,C are free variables. The solution to f0,f1 = 0 allow B and C to be anything. Hence, if I set B,C = 1, I get 1 = 0, a contradiction. Basically, What I showed is that there is no solution of this form such that N ⊂ Q. We can cross this guy out.
Now let's look at
CASE 4:
![[ ]
0 1 0 a
0 0 1 b](Ip2p15ab21x.png) |
which is
| B | = -aD | ||
| C | = -bD |
So
| AD - BC | = 0 | ||
 AD - abD2 AD - abD2 | = 0 |
Let's set set A = 0,D = 1, yielding
| ab | = 0 |
So AD - abD2 = 0 translates to
| AD | = 0 |
A contradiction, since A,D are free. So we can rule out this case
Now for
CASE 5:
![[ ]
1 a 0 b
0 0 1 c](Ip2p15ab23x.png) |
Corresponding to
| A | = -aB + -bD | ||
| C | = -cD |
Plugging into AD - BC = 0,
| AD - BC | = 0 | ||
 (-aB - bD)D - B(-cD) (-aB - bD)D - B(-cD) | = 0 | ||
 - aBD - bD2 + cBD - aBD - bD2 + cBD | = 0 | ||
 (c - a)BD - bD2 (c - a)BD - bD2 | = 0 |
Setting B = 0,D = 1 yields
 |
So (c - a)BD - bD2 = 0 can be written as
| (c - a)BD | = 0 | |||||
 c - a c - a | = 0 | (Setting B,D = 1) ) | ||||
 c c | = a |
So our original solution can be rewritten as
| A | = -aB | ||
| C | = -aD |
I'll call this TYPE J
One last motherfucking case to check, motherfuckers. FUCK. MY HEAD IS FUCKING SPINNINNNNNNNNNNNNG (insert song)
CASE 6:
![[ ]
1 0 a b
0 1 c d](Ip2p15ab30x.png) |
Yielding
| A | = -aC - bD | ||
| B | = -cC - dD |
You know what? I'll just skip the work. You get
| A | = -aC | ||
| B | = -aD |
I'll call this "TYPE K"
Phew, we have a grand total of.... 4 types of lines. Wait, I only wanted 2 types. Errr.... Let's list em all out anyway, along with their matrices:
| TYPE H: | |||
| C | = 0 | ||
| D | = 0 | ||
![[ ]
0 0 1 0
0 0 0 1](Ip2p15ab31x.png) | |||
| TYPE I: | |||
| B | = 0 | ||
| D | = 0 | ||
![[ ]
0 1 0 0
0 0 0 1](Ip2p15ab32x.png) | |||
| TYPE J: | |||
| A | = -lB | ||
| C | = -lD | ||
![[1 l 0 0]
0 0 1 l](Ip2p15ab33x.png) | |||
| TYPE K: | |||
| A | = -mC | ||
| B | = -mD | ||
![[ ]
1 0 m 0
0 1 0 m](Ip2p15ab34x.png) |
Now, again, one issue is that I currently have 4 types instead of 2. I need to group these types together appropriately. But first, I have to check that intersections within each type are empty (otherwise this couldn't be a basis for the partition they're asking for). Remember, when we intersect lines here, we can represent it with a 4x4 matrix that is at leat rank 2. Rank 2 is the 2 dimensional case (the lines coincide), rank 3 is the 1D case (singleton), rank 4 is the 0D case (empty set). If I intersect one type with itself, I want to get rank 4. For example, let me intersect a rank J with itself, which can be represented by:
 |
And if we perform Gauss Jordan elimination on this (assume l0≠l1, otherwise the lines would be the same which is the rank two case)
 | |||
→
 | |||
→
 | |||
→
 | |||
→
 | |||
→
 | |||
Hence a TYPE J intersected with itself is empty, like we need. The argument for TYPE K-K is identical. And TYPE H-H and TYPE I-I are even more trivial
Okay. Now we have to figure out how to group these 4 TYPEs together into just 2 TYPEs. I.e....... we..... have.... to check...... what...... happens..... for each.... type.... intersected..... with.... every.... other.... type....
HEY CS FOLKS. TELL ME: HOW MANY EDGES ARE THERE IN AN UNDIRECTED GRAPH (not counting self edges, since we already handled those). n(n - 1)∕2, you say? YIPPEEE. THAT MEANS WE HAVE TO CHECK 6 FUCKING THINGS
ANOTHER SIX CASE PARADE. ARE YOU READY READER. Now do you see why I want you to pull your pants down. ARRRRRGGHHH! SAVE ME, READER. SAVE ME, WITH YOUR BUTTHOLE. IT'S THE ONLY WAY....I... NEED...... YOUR..... BUTT..... ARRRRRRGGGGHGHH!
CASE 1: TYPEs J-K
 | |||
→
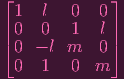 | |||
→
 | |||
→
 | |||
→
 | |||
→
 | |||
→
 | |||
which is rank 3.... assuming l,m≠0 (yeah, uh, to avoid taking this case parade to the next level, I'll let you convince yourself, if you'd like, that things work out if l and/or m equal 0)
So a J-K intersection gives me a singleton. That means they have to be in separate classes.
CASE 2: I-J
 |
Well, that's clearly rank 4. So I-J is empty. (so I and J have to be in the same class.
CASE 3: H-K
 |
Oh clearly rank 4 again. So H-K is empty, meaning H and K have to be in the same class.
That gives us enough information to conclude that our partition should be: I and J are in one class (call this TYPE L), and H and K are in another class (call this TYPE M). Now, to make sure everything works out, I have to check that I get singletons i.e. rank 3s for H-J, I-K, and H-I give me singletons.
(BTW, you may have been able to predict that this is how the types would get partitioned: Compare TYPE J and TYPE I. If you divide both side of TYPE J by -a and you'll see what I mean. Same argument for TYPE K and TYPE H).
CASE 4: H-J
 | |||
→
 | |||
→
 |
Yup.
CASE 5: I-K
 | |||
→
 | |||
→
 |
Yup.
CASE 6: H-I
 | |||
→
 | |||
→
 |
And another YUP! And we're DUN.
I'M TIRED. I'M EXHAUSTED. IT'S BEEN A WEEK. NOW, READER, GIVE ME YOUR BUTT. I'M HUNGRY. *SLURP* RUFF RUFF RUFF. GIMME GIMME GIMME GIMME.