I.5.3
6/15/2021

So we can assume without loss of generality that P = (0, 0) and thus I'll write
μ = μP.
Part a
Let's write f1 = ax + by. From 5.1, we know that P is singular iff
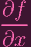 (P) (P) | = 0 | ||
&
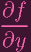 (P) (P) | = 0 | ||
| ⇐⇒ | |||
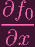 (P) + (P) +
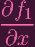 (P) + (P) +
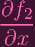 (P) + (P) +
 + +
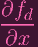 (P) (P) | = 0 | ||
&
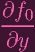 (P) + (P) +
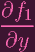 (P) + (P) +
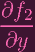 (P) + (P) +
 + +
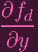 (P) (P) | = 0 | ||
| ⇐⇒ | |||
0 +
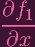 (P) + 0 + (P) + 0 +
 + 0 + 0 | = 0 | ||
&0 +
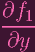 (P) + 0 + (P) + 0 +
 + 0 + 0 | = 0 | ||
| ⇐⇒ | |||
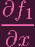 (P) (P) | = 0 | ||
&
 (P) (P) | = 0 | ||
| ⇐⇒ | |||
| a | = 0 | ||
| &b | = 0 | ||
| ⇐⇒ | |||
| f1 | = 0 |
(Those 0s come from the fact that f0 is a constant, so its partial derivative is 0, and the rest of the partial derivatives are homogenous one degree down, so plugging in (0, 0) zeros out all of them except the partials for f1)
I.e. we showed that
| P singular | ⇐⇒f1 = 0 |
In other words,
| P nonsingular | ⇐⇒f1≠0 | ||
| ⇐⇒μ(Y ) ≤ 1 |
As the exercise states, the condition P ∈ Y is equivalent to μ(Y ) > 0⇐⇒μ(Y ) ≥ 1. So
| P nonsingular and P ∈ Y | ⇐⇒μ(Y ) = 1 | ||
Done.
Part b
Here's 5.1. So, ASSUMING THAT THE ONLY SINGULAR POINTS ARE THE
ORIGIN (LOL), all we have to do is look at each equation and take the degree of
the minimum degree monomial
| x4 + y4 - x2 | μ = 2 | ||
| x6 + y6 - xy | μ = 2 | ||
| y2 + x4 + y4 - x3 | μ = 2 | ||
| x4 + y4 - x2y - xy2 | μ = 3 |
Done.