Hello, my loves. Welcome to a new section. Let's start by getting the matching out of the way (just graph them on wolframalpha or something):



The rest has to do with identifying singularities! And this exercise is based on the preliminary definition of (non)singularity:



Now, as the exercise says, each of the varieties given are curves, which means they each have dimension 1. Hence, for each of these, a point is nonsingular iff the rank of the Jacobian is 2 - 1 = 1. I.e. a point is singular iff the rank of the Jacobian is 0. In particular, the Jacobian in each of these examples is gonna look like

J

=

(so really, it's just the gradient vector of f) The rank of the matrix is the row span, which is just a single vector, and that is therefore 1 unless both 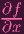and 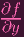are zero. Hence, for each of these problems we are solving

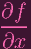	= 0
	= 0

in addition to f = 0, so our solutions actually lie on the curve. Hence this whole exercise is basically solving systems of linear equations (over an algebraically closed field)

"Errr, can't I just look at the graphs and tell from there?" NO. Those graphs are sketches on "real" axes (i.e. non algebraically closed field). Those graphs could be missing some "imaginary"/"complex" singular points, so we do have to go through the algebra (although we do know by looking at the graphs that at least (0, 0) is a singularity for each). See part (c) as an example.

Part a

Here, f = x⁴ + y⁴ - x². The Jacobian matrix is

J

=

Hence, we need

4x3 - 2x	= 0
4y3	= 0

The second equation yields y = 0. And the first equation yields x = 0 or x = ± 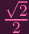. However, (0, 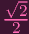) isn't a point on the curve, so the only singular point is (0, 0)

Part b

Here, f = x⁶ + y⁶ - xy. The Jacobian matrix is

J

=

Hence, we need

6x5 - y	= 0
6y5 - x	= 0

Plugging the second into the first yields

6(6y5)5 - y	= 0
66y25 - y	= 0
y(66y24 - 1)	= 0

So y = 0 or y =

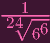
Similarly, x = 0 or x =

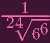
Plugging back each into the curve equation, clearly only (0, 0) satisfies it

Part c

Here, f = x⁴ + y⁴ + y² - x³. So we need

4x3 - 3x2	= 0
4y3 + 2y	= 0

Which factor into

x2(4x - 3)	= 0
2y(y2 + 1)	= 0

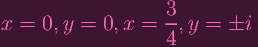By "i" I mean , which is defined because we're in an algebraically closed field.

Plugging in all the possibilities back into the curve equation, (0, 0) obviously works and ( , 0) obviously doesn't. Note that

(-i)4 + (-i)2	= i4 + i2
	= (i2)2 + i2
	= (-1)2 + (-1)
	= 1 - 1
	= 0

Hence, (0,i) and (0,-i) work and ( ,±i) doesn't. So the answers are (0, 0), (0,±i). Note that (0,±i) are points that aren't visible on the "real" graphs on Figure 4.

I cannot fucking figure out how to do part d. The system of equations is

x4 + y4 - x2y - xy2	= 0
4x3 - 2xy - y2	= 0
4y3 - 2xy - x2	= 0

Reader: If you can solve this system of equations nicely, let me know. Otherwise, I'm skipping it.

(BTW: Some 3s and 6s showed up in this post. I was assuming that the characteristic of k wasn't 3, but if you look back you can see that the case of chark = 3 actually gets us to the answers even more quickly)