I.5.1c_ERRATA
6/14/2021
I found a mistake in my work for 5.1c
but I'm not sure how to deal with it:
4x3 - 3x2 = 0
4y3 + 2y = 0
Which factor into
x2(4x - 3) = 0
2y(y2 + 1) = 0
[yielding]
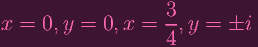
Yeah... that second equation is supposed to be
| 2y(2y2 + 1) | = 0 |
So the actual solutions are
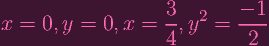 |
Let's test out this new pair of ys then. If we plug it into the curve equation
y2 + x4 + y4 - x3, we get
 + x4 + + x4 +
 - x3 - x3 | (1) | |
=
 + +
 + x4 - x3 + x4 - x3 | (2) | |
=
 + x4 - x3 + x4 - x3 | (3) | |
| (4) |
Clearly, setting x = 0 doesn't work. So the only other possibility is x =
 :
:
 + ( + (
 )4 - ( )4 - (
 )3 )3 | |||
=
 + +
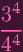 - -
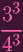 | |||
=
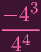 + +
 - -
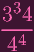 | |||
=
 | |||
=
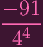 | |||
Which can't be 0 unless -91 = 0. The prime factorization of 91 is 7 ⋅ 13........... which means....... if the field has characteristic 7 or 13........ this is actually....... possible...........?
FUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUCK. Reader: I do not know how to rule these cases out. Maybe I should just accept that (
 , +∕ -
, +∕ -
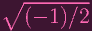 ) actually works if chark = 7 or chark = 13?
Arrrggghh, fuck that. the solution I saw online (which I'm actually not putting
too much trust in atm) said that (0, 0) is the only singular point, so I'm just
going to assume that moving forward for now (i.e. 5.3, COMING SOON)
) actually works if chark = 7 or chark = 13?
Arrrggghh, fuck that. the solution I saw online (which I'm actually not putting
too much trust in atm) said that (0, 0) is the only singular point, so I'm just
going to assume that moving forward for now (i.e. 5.3, COMING SOON)