Now, reader, shall I? that fossil sitting behind your cheekbone teases a hallway of intrigue within. Indeed, it is beckoning me to secrete my secrets into its corridors. Shall I run my tongue across that golden helix? Shall I nibble that lobule, dribble my tongue against that sensitive antitragus, or leave the whole artifact soaked in an indiscriminate slobber? Would it admit my silly trifles, my somber troubles? Would it submit to greedily brandished incisors? Would it forgive a lie; "Don't worry, I don't bite x3"? Would you be so kind as to lend it to me, today? I will give it back, I swear. Pretend my lips are the lips of a seashell, and my warm breath the sound of the ocean. For today I only have one little amulet to donate. One secret. One confession.... I fuked your mom lolololo jk but actually what I was gonna say is i looked at the solution for this exercise. *breathes sex noises into your ear*

I'm sorry, reader. Also, I'm skipping 5.4 because MY ABSTRACT ALGEBRA KNOWLEDGE IS SO FUCKING DEFICIENT LOL.

So, anyway, you may recall that we had a definition for nonsingularity for affine varieties:



In this exercise however, we're working with P², so here's a generalization of the definition for more arbitrary varieties:




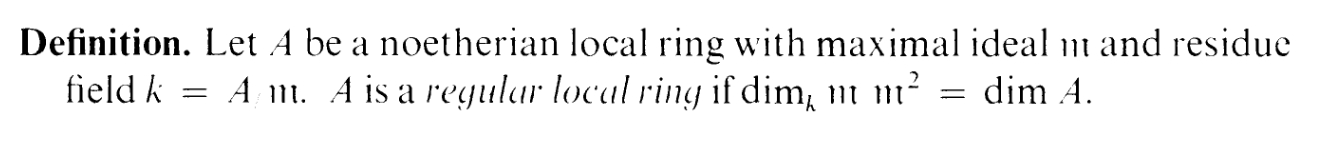
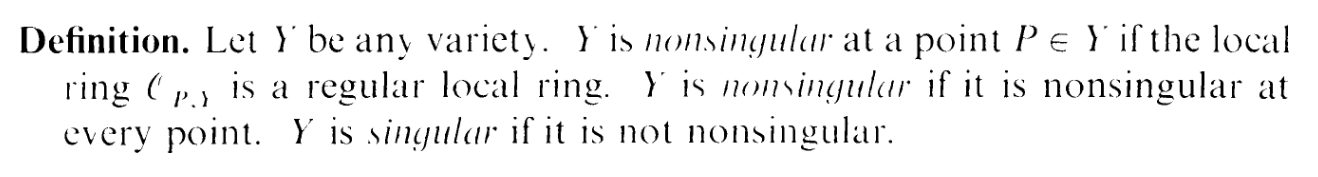
Now, this definition is, as you can see, confusing as fuck. HOWEVER: Note that nonsingularity only depends on the local ring. So we can use open sets in P² instead of P² itself. I.e. we can cover P² with A²s and just default to the more convenient definition with the Jacobian. So this problem is back to checking for nonzero Jacobians.

The solution says that

xd + yd + zd

= 0

(1)

works in almost all cases. Let's take the open set z≠0 (analogous argument for x≠0,y≠0. Then our curve equation turns into

xd + yd + 1

= 0

in A².

The Jacobian is then:

J

=

Now the issue is that if chark divides d, then both components are 0, which is bad! So those are the cases for which this doesn't work, and we'll handle those later. However, in the cases that chark does not divide d, note that we would need x = 0 and y = 0 to make the Jacobian 0. But note that this isn't a point on the original curve, so the Jacobian is always nonzero.



Now we handle the chark|d case. The solution gives

xyd-1 + yzd-1 + zxd-1

= 0

(yea, I wouldn't have thought of this on my own). So taking z≠0, we get

xyd-1 + y + xd-1

= 0

(2)

And the Jacobian is

J	=
	= (since chark|d)

So we need

yd-1	= xd-2	(3)
xyd-2	= 1	(4)

Multiplying both sides of the (4) by y and substuting (3) yields

xyd-1	= y	(5)
xd-1	= y	(6)

Now let's plug in (5) and (6) into the curve equation (2):

xyd-1 + y + xd-1	= 0
y + y + y	= 0
3y	= 0
y	= 0

and thus (6) tells us that x = 0 as well. But this doesn't satisfy (4). Done.