I.3.5
4/20/2021

Oooh, abusive language? I adore abusive language. Like last time, when I said a dense subset contains almost all of
the points. Or when I catcall my local mourning dove.
.jpg)
Or, as it turns out, when in this helpful hint here Hartshorne hoists for his homies (actual math students; not me),
he lets H have degree d. Of course, what he should of said,
for the love of all intensive purposes, is that H = Z(h), where h is a
(homogenous) degree d polynomial. Pfft, I could care less. Hm? What's
that? It has just come to my attention that there are "smart" abuses of language and there are "dumb" abuses of
language. Interesting... I will go ahead research that later (*opens a file named "misc9.txt" and types "abuse of
language" at the top, then doesn't come back around to looking it up*). But really: How algebraic geometrized is my
brain now, that I immediately associate a polynomial with its zero set? Not much, since I still don't even know what
a "scheme" is. But we'll get there, won't we, reader? "Everything that comes out of your mouth is an
abuse of language." Oh snap, haha, nice one, nice one.... WAIT. You mean the smart kind right?
Recall the d-uple embedding? (of course you have, we've seen it like over and over).
| ρ : Pn | → PN | ||
| X = (…,Xi,…) |
 (…,Mi(X),…) (…,Mi(X),…) |
where the Mi are all the d-degree monomials in lexicographic order.
And remember, by 3.4, we know that ρ actually gives an isomorphism of Pn onto the variety S = Z(α) in PN.
Now we're concerned not with all of Pn, but the hypersurface H = Z(h). Now, here's the big clever moment: h is a degree d polynomial, right? So we can actuall write h as
 |
(γi ∈ k). Okay? It gets even better. What does a point X in Z(h) look like? Well, it's a point that satisfies
| h(X) | = 0 | ||
 ∑
i=0Nγ
iMi(X) ∑
i=0Nγ
iMi(X) | = 0 |
BUT, the Mi(X) terms are exactly the coordinates of the image of ρ!!! So, really, letting the coordinate ring of PN be k[y0,…yN], we can write the image of H under ρ to be Z(f) ∩ S, where
| f | = ∑ i=0Nγ iyi |
So ρ maps H onto Z(f) ∩ S. Which means that it maps Pn - H onto S - (Z(f) ∩ S). It's trivial to see that an isomorphism of varities induces an isomorphism on the open sets, so we can in fact write
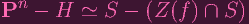 |
Okay, now what? This is where it gets kinda complicated.
First realization is noticing that we're actually looking at the intersection of a variety with the complement of a
hyperplane. That is, we can rewrite the above as
 |
Let's set S ∩ (PN - Z(f)), and Y = PN - Z(f), so that R = S ∩ Y . We want to show that R is affine. Now...
Hmmm... "the intersection of a variety with the complement of a hyperplane". This is reminiscent of another
situation, isn't it? f, of course, is a linear polynomial. So, you know what? Let's trust my instincts. .... Uh reader...
Why are you running away..? Reader, no!!! My instincts aren't always "wrong with a tinge of serial killer"!!!
READER NOOOOOOOOOOO!!! COME BACK.
...For now, let's just ASSUME that we have a isomorphism ϕ that takes the hyperplane Z(f) to the hyperplane
Z(x0). So ϕ isomorphically carries PN onto itself in a way that maps S onto some variety S′, and
Y = PN - Z(f) onto U = PN - Z(x0). And, by the way, last set, U, is definitely affine thanks to old prop 2.2:

So that's what the hint was referring to. So, now looking at R, we get that R = S ∩Y gets mapped isomorphically
to S′∩ U. And this variety is affine thanks to corollary 2.3!
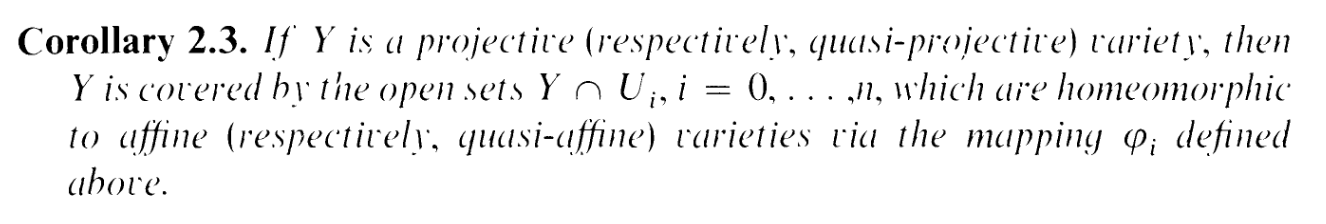
In conclusion:
| Pn - Z(h) |
 ∩ (PN ∩ Z(f)) ∩ (PN ∩ Z(f)) | |||||
 ∩ (PN ∩ Z(y
0)) ∩ (PN ∩ Z(y
0)) | ||||||
| ≃ Z ∩ AN | (Z an affine variety in AN) |
So, okay then. What about that ϕ guy ("phi guy", like "high guy" cause it's 4/20, LOLOLOLOLOLOLO LOLOLOLOLOLOLOOO lOOOOOOOOLOOOO OOOOOOOO OOOOOOOO OOOOOOOOOOOOOOOOOOOOOLOLOLOLOL OLO LO LOL OL OL OLOL OLOOOOOOOOOOO LOLOLOL LOL OLOLO LOLOL OLOL OLOLOL OLOLOLOLOLOLOLOLOLO. FIUCK. FUCK. FUCK,. FUUUUUUUU UUUUUUUU UUUCK. HELP ME. I'M GONNA FUCKINGG DIE. I'M GONNA FUCKING DIE. I'VE NEVER EVEN SMOKED WEED) We need to actually construct an isomorphism that maps ∑ i=0Nγiyi = 0 to y0 = 0.
Well, if you think about it, that is basically just rotating a plane about the origin, right? So ϕ should be an (invertible) linear transformation that maps a basis for the the first to one for the second. And invertible linear transformations are def isomorphisms (see here). So we're DONE.