I'm late, but welcome back. This exercise has a smooth start and a rough ending. Begin, reader, by comparing part (c) and part (a). Turns out: Conics in projective space act more nicely than conics in affine space. All conics are isomorphic to each other, and to P¹.

Now, to start this exercise off, it would be nice if we could start by showing that all conics are isomorphic to each other, by reducing them to some "standard form". Back in 1.1c, I essentially showed that translations (LEMMA 2) and invertible linear transformations (LEMMA 3) ("rotations") are isomorphisms.

Now, one big issue with my work there is that I kind of just "assumed" that a series of such translations and rotations would get us to standard form, without actually showing how. I did link a Wikipedia page that claims this to be true, but ain't that one hell of a cop out? In fact, if I just assumed this, then it turns out that a huge segment of my work is actually extraneous. And anyway, that page appears to be discussing the specific case of when our field is ℝ (whereas we're working over an algebraically closed field k).

...I probably need to make another post just to fix that. HOWEVER: We'll leave that for another day. Today, we're going to be thorough for the nice, sexy projective case.

Okay, so let's work in P² for now. First thing's first: It appears that, actually, translations are generally not isomorphisms in projective space. A very simple example is that if you translate all the points of Z(f) by, say, adding T to all of them, then the new set S can be written as Z(f_T) where, as in 1.1c,

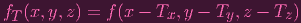Which, in general, is a nonhomogenous polynomial (e.g., think of the case f = x,T = (1, 0, 0)), and I don't see a good way of constructing a homogenous set of generators for S

HOWEVER: We do not need translations. The power of projective space allows us to get all the conics merely via means of linear transformation ("rotation").

One folly of this exercise is that it doesn't actually define what a "conic" is for projective space. So I'll give you a definition: A conic in P² is the zero set of an irreducible homogenous quadratic (definitely has to be irreducible, or else there's no way the zero set is gonna be isomorphic to P¹, lol). So, in general homogenous quadratic's zero set is going to look like this:

Ax2 + Bxy + Cy2 + Dxz + Eyz + Fz2	= 0
	= 0
xTAx	= 0

(sry for reusing the same variable name for different things. YOU CAN FIGURE IT OUT)

The key point here is that we can diagonalize A, writing it as A = P^-1DP where D is a diagonal matrix, and P can be chosen as an orthogonal matrix (since A is symmetric!), so P^-1 = P^T, and therefore, we can write

xTAx	= xTPTDPx
	= (Px)TD(Px)

if you look closely, you can think of this diagonalization as converting to a new quadratic by applying the change of basis P on x (see here). Hence, if we show that invertible linear transformations are isomorphisms, we can assume that all conics can be represented by the simpler standard form

Ax2 + Cy2 + Fz2	= 0

Furthermore, with the linear transformation



(note that since we're in an algebraically closed field, such square roots exist, and yes, A,B,C have to all be nonzero, otherwise the conic would be reducible), we can actually assume that our conic looks like

x2 + y2 + z2

= 0

SO: simple linear transformations are sufficient to make all conics isomorphic to each other... provided that (invertible) linear transformations are isomorphisms. Well, are they?

First of all, note that unlike for translations, linear transformations do map homogenous polynomials to homogenous polynomials: An arbitrary linear transformation can be represented by

x	a1x + a2y + a3z
y	b1x + b2y + b3z
z	c1x + c2y + c3z

and so given a homogenous polynomial γ_ix^a_iy^b_iz^c_i, the corresponding polynomial can be written as

γi(a1x + a2y + a3z)ai(b1x + b2y + b3z)ai(c1x + c2y + c3z)ai

which is homogenous by the binomial theorem

Now, following my 1.1c notation, given a linear transformation L, I denote the polynomial given by applying L^-1 on the coordinates as f_L (So f_L(P) = f(L^-1P).

Now, it's clear that for a point P ∈ P², f(P) = 0⇐⇒f_L(LP) = 0.



So letting

ϕL : P2	→ P2
P	LP

be the linear transformation by L, and correspondingly letting

ψL : k[x,y,z]	→ k[x,y,z]
f	→ fL

be the k-algebra isomorphism of coordinate rings, it's clear that, given a variety X, ψ_L gives a homeomorphism between X and Y = ϕ_L(X)

Now, back in 3.1a, I could use the isomorphism of coordinate rings induced by ψ to conclude isomorphism between X and Y , but of course, Corollary 3.7 only applies to affine varities. So I have to show the isomorphism manually. No worries: the homeomorphism part is already done, so I just have to show that pesky regularity property.

Suppose V ⊂ Y is open, and f : V → k is regular. Then I need to show that f ∘ϕ_L : ϕ_L^-1(V ) → k is regular. But given an open U ⊂ V where f = g∕h on U, then for any P ∈ ϕ_L^-1(U),

f ∘ ϕL(P)	=
	=
	=

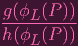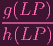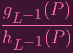hence it's locally rational, therefore regular. So ϕ_L is a morphism. DONE.

And what about showing that the inverse map ϕ_L^-1 is a morphism? Muahaha. Guess what. ϕ_L^-1 is just ϕ_L^-1. That's right: the exact same logic proves that it's a morphism. hence ϕ_L is an isomorphism. I.e. linear transformations of varieties in P³ are isomorphisms (actually, the same argument applies to Pⁿ).

And, recall, since all conics in projective space can be linearly transformed into one another (in particular, into x² + y² + z² = 0), all projective conics are isomorphic to each other. Great. Now I just have to show that one of these conics is isomorphic to P¹.

This is where I got stuck for 7 days.

You, see, I tried all sorts of nifty tricks trying to show that Z(x² + y² + z²) ≃ P¹. I tried covering it with affines and gluing the maps together, I tried to visualize a cone being mapped into the projective line, I tried to parametrize the nonreal unit sphere, then the nonreal unit hemisphere.

Then I finally looked up a solution.

Guess what? Trying to construct the isomorphism from Z(x² + y² + z²) is a bad idea. Remember? You can make the isomorphism from any irreducible conic. Why was I so stubbornly sticking to this one? I mean, you have to forgive me somewhat for trying. After all, it's the super special (that's why you are here with me (miracle baby pornography superstar)) diagonalized form–the very form that all conics can "reduce to" via a simple procedure. But insofar as producing an isomorphism with P¹, it's a huge pain: The squares in particular get in the way like a motherfucker. Of course, there's some way to get an isomorphism directly from Z(x² + y² + z²), but it's a pain.

The better choice of a conic is actually Z(xz - y²). This is what the solution I read used, in any case. Now, this might seem like an arbitrary choice at first glance. Why would it be any better than the special diagonalized form? Well, honestly, it's kind of appalling that I didn't try this out. First of all, if you remember 3.1a, I actually used the affine version of this curve to produce an isomorphism. Why didn't I think of doing the same here in projective space? And here's another thing: While aimlessly making up crazy martial arts to try and produce a map, for some reason I never looked back at the exercises in section 2 to see if they would be of any help. This part of the exercise is about projective space, AND I NEVER THOUGHT TO LOOK BACK AT THE SECTION THAT WAS ALL ABOUT PROJECTIVE SPACE. Instead, I wasted more and more time trying to do super hyper cartwheel backflips through this only to repeatedly land on my butt and dance around the room clenching my buttocks in pain then ending up in a fail compilation which leads to this post getting licensed by Jukin media and getting bombarded by comments saying, "The stupidity of Americans today never fails to astound me", written by someone whose profile picture is the old default Youtube silhouette with a spider on it. My foot is finally in the door to becoming a lolcow.

I am, indeed, butthurt. But, hindsight now tells me that 2.12 exists. And, in fact, now that I've done 3.4, noticing that Z(xz - y²) is simply the 2-uple embedding of P¹ in P² (as it says in the very exposition of 2.12) finishes this exercise.