What a terrifying series of gaps. 3/11/21 → 3/23/21 → 3/31/21. Look at that: I'm making a platformer, and this is one of those auto-scrolling levels. And believe me, you don't want to fall into the depths between those flat-top mushroom towers. I can't tell you what lies between there, all I'll say is if on the way down you see a bottle saying "PINK MARMALADE", ignore it.

So we're approaching the turn of the month, with little to show for it. I've "ripped myself off in spring" ← This is my spin off of the title of a post I read today, by Neocitizen Dann. Dann writes:

Now, one justification to the reduction of festivity frequency is that, time feels much slower for children. Like, half of what adults say nowadays is just, "What!? How is it already almost April!!!" I get it. I'm getting used to being surprised at time flying. It ain't good. But you see, for kids, there is a downside to time passing slower: since every month feels like a year, getting through a month is 12x more tough. Hence, Dann's beloved monthly grade school celebrations. Without some kind of thing to look forward to to cap off each month, children wouldn't have any motivation to stay on track.

...Well, I think that's right. That's probably right. But a liiiiiiitle part of me, the kiddish part of me, suggests, whispers in my ear, that maybe that's not quite it? Well, shota me isn't very trustworthy, so maybe we should ignore him. On the other hand, current me is even less trustworthy... Okay, fine, let's hear what my 6 year old self has to say:



Well, Xx_DarkSlicer_xX, I regret bringing you onto this site. You aren't very trustworthy, after all. Also, I know you're still young and it's the early 2000s for you, but in our time, it's not okay to use "gay" as an insult.



Idiot. That's not a "riddle". You don't know what that word means. But I see what you're going for. As an adult, everything feels too short in general. Yet, in relative terms, October, November, December feel like the longer months. Especially December. Especially the last two weeks of December.



Right. For a large part of my adult life, I've felt Scroogey about Xmas. It wasn't until 2016 where, due to circumstances, I warmed up to the holiday, and that I felt that the weeks leading up to it were so long. Right: I can extrapolate. Like, say, when you're excited for a concert, the weeks leading up to that concert feel like ages.



............

Okay, loser. Another example: When you're excited for a package to arrive, even if the delivery time is like less than a week, it feels like a long wait (hence the compulsion for many people to repeatedly check the delivery status). Or, say, when I was your age (i.e. when I was you, lol), I remember how waiting for the release date of certain games felt like running a marathon. Oh, and the march to the deadline for a big project is as slow as the project is big ← this particular example has been captured very well by anime such as Sakurasou (season 1) and New Game, as well as the VN Kira Kira (common route).

NO FUTURE

It's not really even the fact that something exciting or great has to be waiting at the end of the selected period. Just something, say, relieving. Something to build up to. On a per-day basis, the weekdays feel longer than the weekends. Perhaps because on the weekdays, you're waiting for the weekend? Even within a day you can record this phenomenon: A workday feels long because the drudgery of the work is contraposed with the longing for it's end. A boring meeting takes forever because you can't fucking wait for it end: those last 5 minutes can be exhilirating, and finally getting out of icebreaker hell and breathing fresh air feels heavenly.

Here's David Foster Wallace, whose books I will never read, in a footnote from his speech/essay Laughing With Kafka:



Oof (the Roblox type). Ain't that a shame, eh, Xx_DarkSlicer_xX?



But that's adulthood. What can you do? "It was becoming obvious that not everything was equal, and that childhood reverence had a firm shelf life," Dann writes, on the fading excitement over non-"big three" holidays. Adulthood is coming to terms with the fact that life isn't all fun and games. Or, at least, as DFW points out, that's modern American adulthood. Is that adulthood in general?

Hey, this is gonna sound outdated, like, 500-323 B.C. level stuff, but... didn't Classical Athens have, like, monthly festivals? Oh, actually, it was even worse (better?): Almost half the days in a year were made up of feasts and festivals. Classical Athens was the party school of ancient Greek city-states, baby (clearly, putting those Delian League payments to good use). You think monthly grade school festivities are childish? You think frat boys and woo girls and incessant college house parties are immature? Western civilization was founded on a culture of partying. WOOOOOOOOO. A good nu-adult might scoff at the pink on Valentine's day, the green on Saint Patrick's. Sounds silly. But rollback to the fountain of your culture and you have a Demeterian festival for just the gurls, the late spring festival of Dionysus for the screening of 4 big plays, etc. Athenians sure didn't get "ripped off in spring", eh? Were they onto something?

So, 6-year old me, what is an adult who feels their youth slipping away to do? How is one to apply the apparent phenomenon of time flying being inversely related to degree of anticipation?



Me neither, mate. Me neither. Anyway, since you're here, wanna try some selfcest?




Anyway, that was basically my roundabout excuse for the delay of this exercise... LET'S GET ON WITH IT.
Here's the exercise again:



Last time, I was hyping up the fact that every conic (in A²) can be thought of as just a parabola or a hyperbola (by the way, I will mention that I realized recently that I did a lot of unnecessary work, or rather that I showed the wrong work to get there... I might have to make an errata page for that... Fuck). What we showed last time is that the coordinate ring of any conic is either A = k[x,y]∕(y - x²) or B = k[x,y]∕(xy - 1). Now let me give you the goods you've been waiting for:



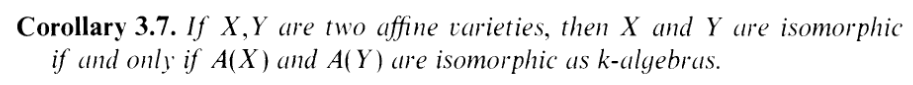
That corollary tells us that isomorphic coordinate rings is equivalent to isomorphic (affine) varieties. And thus, we can conclude, in fact, that every (irreducible) conic is isomorphic to either Z(y - x²) or Z(xy - 1). I.E. Every conic is a parabola or hyperbola.

"But what do you mean by isomorphic?" This:



And what does "regular" mean??? This:



"I don't get it." Heh. Fool. Me neither. But we didn't come here to understand, did we? Think of it as "homeomorphic" with a little extra sugar. This "regular" business–I would say that it means that "a function can be expressed locally as a rational function." OR: since open sets are dense, maybe "a function that can be expressed densely as a rational function" may be more appropriate. Regular = "Locally/densely rational". And a morphism? It takes regular functions to regular functions. What's the motivation for all this? Pffffft. Who needs motivation when you have cunny? (I have neither).

So anyway, by whatever that standard means, every conic is either a hyperbola or parabola. Now, this exercise wants me to do one better: Show that every conic is either A¹ or A¹ -{0}.

A¹ or A¹ -{0}, huh? The affine line and the affine line with the origin removed. So.... Which one is the parabola and which one is the hyperbola? Answer: Look back at 1.1a (just look at the exercise, not my shitty writing): Letting Z(y - x²), I know A(Y ) ≃ k[w]. And since k[w] is the coordinate ring of A¹, Corollar 3.7 tells me that Z(y - x²) ≃ A¹. Cool, the parabola is isomorphic to the affine line.

Now I just have to show that the hyperbola Y = Z(xy - 1) is isomorphic to X = A¹ -{0}. Now, this time I can't just equate coordinate rings. Why? Well, Y is an affine variety. But X is not an affine variety (closed set). It's a quasi-affine variety (open set). So what do?

Well, it's a "Corollary", which means that it must be attached to some proposition. Here it is:



So I would now like to find a k-algebra isomorphism between A(Y ) and (X)

"What's (X)?" It's defined as the ring of all regular functions on X.

If we let k[w] be the coordinate ring for A¹. Since w and its powers are the only functions that are nonzero on X = A¹ -{0}, then clearly (X) = k[w]_w, the localization of k[w] by w (k[w]_w = { 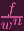|f ∈ k[w],n ≥ 0}).

Hence, I'd like to show that A(Y ) 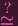k[w]_w i.e. k[x,y]∕(xy - 1) 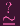k[w]_w. Which means that I'd like to make a k-algebra morphism

whose kernel is (xy - 1). Doing some meme algebra, xy - 1 = 0 y = 1∕x, so that implies that we should define

ϕ(x)	= w
ϕ(y)	= 1∕w

So clearly (xy - 1) ⊂ ker ϕ, and for the reverse inclusion I'm going to do the typical Euclidean division argument: Given f ∈ ker ϕ, think of f as an element of k[x][y], so dividing by xy - 1 yields

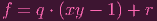where r ∈ k[x]. Taking ϕ of both sides yields ϕ(r) = 0. And clearly ϕ(r) = 0⇐⇒r = 0, so f = q ⋅ (xy - 1) which means that f ∈ (xy - 1)

Dun. So ϕ : A(Y ) → (X) is an isomorphism.

Now, proposition 3.5 tells me that this induces a morphism ψ : X → Y . Since ϕ was an isomorphism, ψ should be an isomorphism.... Right? R-right?

*Sigh*... Well, it doesn't really tell me that directly. All it says is that there's a "bijective mapping". Or a "natural" bijective mapping, whatever the fuck that means.

Yep, I guess I have to verify it manually. The definition of ψ is straightforward (given by the proof of the proposition):

ψ : A1 -{0}	→ Z(xy - 1)
W	(W, 1∕W)

And I know it's a morphism, and it's clearly bijective. So now I have to verify that the inverse mapping is a morphism. The inverse map is clearly:

δ : Z(xy - 1)	→ A1 -{0}
(X,Y )	X

(Yes, I accidentally reused X and Y for the coordinates even though I was using them to refer to the spaces. Woops. I'll let you distinguish, reader). Now the question is: Is it a morphism?

Well, first, I need to verify that it's continuous, which is equivalent to verifying that ψ : X → Y is a closed map. So give me a closed set Z(f) in A¹, (so Z(f) ∩ X is a closed set in X). Then, is S = ψ(Z(f) ∩ X) closed in Y = Z(xy - 1)?

Note that f(w) ∈ k[w], so if I define g(x) ∈ k[x] to be f but with the ws replaced by xs, and h(x,y) ∈ k[x,y] to be identical to g, (just living in a different coordinate ring). then clearly f(W) = 0⇐⇒g(W) = 0⇐⇒h(W, 1∕W) = 0⇐⇒h(ψ(W)) = 0. So ψ(W) ∈ S⇐⇒f(W) = 0⇐⇒h(ψ(W)) = 0⇐⇒ψ(W) ∈ Z(h)⇐⇒ψ(W) ∈ Z(h) ∩ Y . Hence S = Z(h) ∩ Y , where the latter is a closed set in Y .

So δ : Y → X is continuous, which means that ϕ is a homeomorphism. But now we need the "extra sugar": We need to show that whole "rational to rational" thingy for δ.

Suppose V ⊂ X open and f ∈ (V ). Then I need to show that

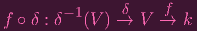is regular.

Since f is regular, let U be an open subset of V where f = g∕h, where g,h ∈ k[w] (h nonzero on U). Let g′,h′∈ k[x,y] be g and h except with the ws replaced with xs (so they don't have any ys), so g(W) = g′(W, 1∕W) and h(W) = h′(W, 1∕W). Then clearly h′ is nonzero on δ^-1(U) and f ∘δ = g′∕h′ on δ^-1(U) and is hence regular.

DUN. See you in part (b)... though since I'm """busy""" expect updates to be slo, for the next week or two. Ahh, gaps. Ahh, platformers. Also looks like the "sheaf" symbol came out as black each time. Whatever. It represents the dark state of my understanding regarding that concept.