Let's follow the hint. For now let's just assume that (X) ≃ k[x,y]. Then if X were isomorphic to an affine variety Y , then we'd have that (Y ) ≃ (X) (see Lemma 1, here. Hence (Y ) ≃ k[x,y], which means that we must have that Y ≃ A² (corollary 3.7). Hence, X ≃ A². Let's call this isomorphism ϕ:

ϕ : A2	→ A2 - 0

Now, the question being begged is if ϕ maps A² to A² - 0, where is the origin being mapped to? It has to be mapped somewhere, so let's suppose that ϕ(0, 0) = (R,S)

Now, nothing immediately wrong with that persay. There are isomorphisms of affines that map the origin to nonzero points. Like translations for example, like I've shown before. But WAIT: This map couldn't be a translation. Because then what would (-R,-S) map to? HMMMMMMM.

Something is geometrically wrong with this map. And since this subject is called "algebraic geometry", let's look at what's happening with the induced map of coordinate rings:

ϕ* : k[x,y]	→ k[x,y]
f	f ∘ ϕ

This map is an isomorphism (again, thanks to Lemma 1 from here). And how is it defined? Well, figuring out how a k-algebra morphism means figuring out where x and y go. Let's start with x.

x	ϕ * (x)
	= x ∘ ϕ
	∈ k[x,y]

Errr... okay.... Let's try plugging in the special point (0, 0), in which case we get that

(x ∘ ϕ)(0, 0)	= x(ϕ(0, 0))
	= x(R,S)
	= R

Ah, so ϕ * (x) has to be a polynomial that evaluates to R on (0, 0). Which means that it must be a polynomial with a constant term of R:

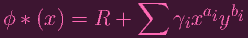(1)

Okay, that thing on the right is kind of complicated. But I believe! I believe that it's simpler than that. Remember: I had a strong suspicion that this map would end up representing a translation. could the right hand side, possibly, be simply x + R?

Well: ϕ* is an isomorphism. Okay. And the fact that ϕ maps (0, 0) to (R,S) is equivalent to saying that ϕ* maps (x,y) to (x - R,y - S). In particular, it has to map the generators of the former ideal, x,y to generators of the latter ideal.

NOW: are the generators of the latter ideal necessarily x - R and y - S? Not necessarily. But it's pretty clear to see that they have to be at least linear. So I can write (1) as

ϕ * (x)

= R + ax + by

Similarly, I can write

ϕ * (y)

= S + cx + dy

OKAY: sooooooo this isn't quite a translation..... BUT, this does tell us that ϕ must look like this:

(x,y)

(R + ax + by,S + cx + dy)

And remember: The contradiction I'm looking for is to produce a 0 in the image. Is that possible? Well, I would like.

ax + by	= -R
cx + dy	= -S

BUAHAHAHAHAHA. A system of linear equations. And it's clear to see that it must have full rank (remember we need to generate the maximal ideal (x - R,y - S), and thus has a solution.

SO WE'RE DONE....

Dick: Welcome to Dick & Cock United, where we bring you the highest quality Dick & Cock goods. I'm Dick

Cock: And I'm Cock.

Dick: And together, of course, we're Dick & Cock.

Cock: Hey Dick.

Dick: What's up, Cock?

Cock: Let's play a game. When I say Dick, you say Cock. Got it? I'll start: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Dick: Cock.

Cock: Dick.

Cock: Good stuff, Dick. Gimme a high five.

*Clap*

Dick: Down low!

*Slap*

Dick: Too slow.

Cock: Too small.

Hi. So I decided to check for myself just how "pretty clear" it was that the images must be linear. Of course, this resulted in me spending 2 days trying to "check" this. I spent fucking hours. Hours spent messing around with summations, exponents, indices.......... and then discovered that it's not even true. Which means that, as you can tell from the mega strikethrough, we have to go all the way back to (1):

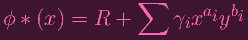Let's call this f. And let's write an analogous polynomial for ϕ * (y)

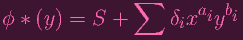Let's call this g. So I can't necessarily claim that f and g are linear (thus screwing up the "translation" dream). In fact, this is sort of the best I can do unless I want to use the advanced "automorphism theorem of k[x,y]" linked above. Fine then I'll have to do with using that as my base map. If that's what ϕ* is, then ϕ is given by

(x,y)	(R + ∑ γixaiybi,S + ∑ δixaiybi)
	= (f(x,y),g(x,y))

Now, why did I want translation or linearity in the first place? I wanted to produce (0, 0) in the image, to yield a contradiction. Indeed, I would like to find a point (x,y) that is zero on both polynomials. I.e. I want Z(f) ∩ Z(g) to be nonempty. Here's the thing. we know that ϕ* maps x f and y g. So ϕ must map (Z(x) ∩ Z(y)) to Z(f) ∩ Z(g). But the former set is nonempty (it contains (0, 0)), so since ϕ is an isomorphism, the latter set must be nonempty too.

So there you fucking go. FUCKING DONE.

actually, we still need to show that (X) ≃ k[x,y].... Fuck.



Alright. Fine. So (X) = S^-1k[x,y] where S = {f|f≠0 on X}. Now let's suppose that f ∈ S. If f is reducible, then it can be factored into f = g ⋅ h where both g and h must be in S. So let's assume without loss of generality that f is irreducible. Then f must be nonzero on all of A², possibly excluding the origin. Well, if it has no zeros at all, then it would have to be a constant function (f ∈ k). What if it was 0 at the origin, and only the origin? Then f(x, 1) would have to be a constant polynomial (otherwise f(x, 1) would have zeros. Say it had a zero at a. Then (a, 1) would be a zero of f, contradicting nonzeroness outside the origin). Actually, this would apply for any f(x,b) where b ∈ k. And I'm PRETTY SURE that this means that f has no x terms. I know we JUST saw the consequences of trusting my "pretty sure"ness, but.... I've already spent way too much time on this. Exercise left to you, dear reader, lol (I'll hoist a hint for you: plug in 1 and then a large value a >> 1 for y and see what happens to the like degree x terms in either case.). If you apply this same "reasoning" to show that f has no y terms either, that means that f ∈ k yet again. Hence, S = k. Which means that S^-1k[x,y] = k[x,y]. DONE.