I.3.17a
5/19/2021
Spelled out, this means that if x is an element of the field of
fractions of A which is a root of a monic polynomial with coefficients in A, then x
is itself an element of A. 
"What happened to 3.16?" I did it. I even made a huge post for it and uploaded
it. Except, it was one of the cringiest things I had ever written. The post went live
for approximately 1 hour on 5/17 before I took it down in embarassment.
I spent hours typing it up and editing and polishing it, only to realize
that it was a disgusting, unsalvageable insult to humanity, and removed
the whole thing. I am truly sorry for anyone who had the unfortunate
experience of happening on my page during that hour and reading that horrific
piece of work. I suggest those that are still sufferring side effects from
the cringe visit a trauma center or at least try out a session of therapy.
Yes, it was bad. I almost deleted my entire page because it was so bad.
If you're curious as to what it was about, I'll just say two words: Bill
Murray. Yes, I'm not kidding. I am still shudderring, thinking about how I
actually typed "Hurrah for Bill Murrah, Hurrah for Bill Murrah," as if it
were funny. Not to mention my LARPing as an internet sleuthster and...
*gag*.. that "inspirational quote" I put in there. My fucking god, that was
horrific. My fucking god. I know this site is always cringe, but 3.16 was too
much, even for me. I apologize from the bottom of my heart again to
anyone that had to see that. That horrific 1 hour cannot be recompensed;
we can only beat on into the future, against the tides of unfunniness.
Anyway, for this exercise we obviously have to use this theorem:

And we have to show that
 P is integrally closed. What does that mean? Well,
Wikipedia says that there are two possible definitions for this.
P is integrally closed. What does that mean? Well,
Wikipedia says that there are two possible definitions for this.
Which one is it? 1 or 2? Everyone write down your guesses on a piece of
paper! I will reveal to you the answer in approximately 10 dots from here.
.
.
.
.
.
.
.
.
.
.
.
.
Alright, alright, times up, haha. Fill in your guesses everyone. Okay, everyone
ready? Here we are. If you guessed neither, then you're correct! Yaaaay! Huh,
no one guessed that? Strange.
Yes, the thing we're actually looking for is this. Granted, it is "related" to the first
definition from above, but not transparently enough for me to give it credit. Why
isn't it listed on the disambiguation page?? At least the description here is good:
Okay, we need to show that ALL projective conics have integrally closed local
rings? Sounds daunting, but remember from 3.1b that all projective conics are
isomorphic, so we just need to show this for ONE (1) projective conic. Hold on.
*Cringes to the side as I briefly recall how bad 3.16 was
Oops, sorry about that. It's still kind of bothering me. Anyway, now comes
the first difficult step: Which conic should we choose?. You may recall
that back in 3.1c, I'd chosen the "wrong" conic to try and solve that
exercise. So, which conic do you think we should use? The "standard"
x2 + y2 + z2 = 0? Or perhaps the xz - y2 that saved me in 3.1c? Or maybe
another homogenous quadratic would be more appropriate here? Everyone write
down your guesses and I'll be back in about 10 dots with the answer.
.
.
.
.
.
.
.
.
.
.
.
.
Alright! Time's up! Dot your i's, cross your t's!. Ok, ok. Everyone finished? If you
guessed none of them, then you'd be correct! Huh? Everyone guessed this one
right? Well, you folks learn quickly, eh?
That's right: 3.1b says that all conics are isomorphic to each other... via being
isomorphic to P1. So the space we actually want to take the local ring of is
obviously the much easier P1. "Obviously" I say, but I actually had to look at the
solution for this. I cannot fucking believe I didn't think about this myself. "If
multiple things are isomorphic, use the most convenient local ring" Okay, SO
WHY DIDN'T I USE P1?????? WHY WAS I DECIDING BETWEEN "THIS
CONIC" AND "THAT CONIC" LIKE SOME FUCKING IDIOT? WHY AM I
THIS FUCKING STUPID? ALSO,
*Vomits into a bucket as I recall how in 3.16 I tried to
"start" a meme about Bill Murray that had already been
well-established elsewhere
Just a dogpile of stupidity today, aren't we? It doesn't end here. Let me show that
 P is an integrally closed domain for Y = P1. Prepare for more stupidity.
P is an integrally closed domain for Y = P1. Prepare for more stupidity.
So let P ∈ Y . Then thanks to theorem 3.4b,
 P = S(Y )mp, where
P = S(Y )mp, where
| mp | = ({g ∈ S(Y )| g is homogenous, g(P) = 0 }) |
Now let K be the field of fractions of
 P. Following the "spelled out" definition
above, let's suppose that h ∈ K satisfies
P. Following the "spelled out" definition
above, let's suppose that h ∈ K satisfies | H | = xn + c
n-1xn-1 +
 + c
1x + c0 + c
1x + c0 |
where ci ∈
 P. So H(h) = 0, i.e.
P. So H(h) = 0, i.e. | 0 | = hn + c
n-1hn-1 +
 + c
1h + c0 + c
1h + c0 | (1) |
Since h ∈ K, we can write h =
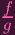 ∕
∕
 , where f,a ∈ S(Y ) and g,b ∈ S(Y ) -mp
(S(Y ) here is simply k[x,y], since Y = P1).
, where f,a ∈ S(Y ) and g,b ∈ S(Y ) -mp
(S(Y ) here is simply k[x,y], since Y = P1). *Shivers as I recall how for 3.16, I made up a Bill Murray story that wasn't funny, so I tried to replace it with a "better" story that turned out to be even worse, and I ended up using the worser story in the "final product" as an "おまけ".
Now, here's my thinking: If I prove that a ∈ S(Y ) -mp, then
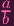 is invertible, so
I can write h as h =
is invertible, so
I can write h as h =
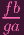 , which is an element of
, which is an element of
 P, and I'd be done. Now P is
a projective point, but let's take any representation of it. Then clearly g(P) = 0
for any g ∈ mP. So if I just show that a(P)≠0, I'm actually done.
So what should I do? I'll suppose a(P) = 0 and get a contradiction.
P, and I'd be done. Now P is
a projective point, but let's take any representation of it. Then clearly g(P) = 0
for any g ∈ mP. So if I just show that a(P)≠0, I'm actually done.
So what should I do? I'll suppose a(P) = 0 and get a contradiction.
You see (1)? Let me multiply both sides of that equation by a∕b.
If you cancel out the denominators of the h terms, you obtain
| 0 | = (f∕g)n + c
n-1(a∕b)(f∕g)n-1 +
 + c
1(a∕b)n-1(f∕g) + c
0(a∕b)n + c
1(a∕b)n-1(f∕g) + c
0(a∕b)n | (2) |
*Shudders as I think of all the lives that were lost during "The Dark Hour", also known as the "Murray-holeinmyheart Incident"–those fated 60 or so minutes in which 3.16 went live and took God knows how many innocent readers in its crushing path. Statisticians are still trying to calculate the full extent of the damage. Some figures say up to 6 million readers may have been lost. 5/17, never forget.
Now plug in P, and note that since a(P) = 0 by assumption, all the terms vanish except the first, so we have,
| 0 | = (f(P)∕g(P))n | (3) |
Which implies that
| f(P) | = 0 |
Now lets plug in P into (1). This time, since all the h's have f in the numerator, every term vanishes except for the last one. So (1) actually turns into
| 0 | = hn + c
n-1hn-1 +
 + c
1h + c
1h | (4) |
*Wipes tear from eye as I remember uploading 3.16 and realizing what a horrible mistake I had made. I recall, during that fated hour, frantically editing it and trying to salvage it from its godawful unfunniness, but it was too late. The post was just fundamentally such a disgrace to humanity that I had to remove the whole damn thing. 5/17, never forget.
But we can factor out an h from this equation, yielding
| 0 | = h(hn-1 + c
n-1hn-2 +
 + c
2h + c1) + c
2h + c1) | ||
Now, if h = 0, we have h ∈
 P, which is the trivial solution. But in the case
that
P, which is the trivial solution. But in the case
that | 0 | = hn-1 + c
n-1hn-2 +
 + c
2h + c1 + c
2h + c1 |
This is just the same case that we started with, except one degree down. So we can keep whittling down degrees until we're left with
| 0 | = h |
Which again, is the trivial case.
Annnnd that's this exercise! Except... that makes no fucking sense whatsoever. You see, because of my stupidity, I had started this exercise by attempting to show it for an actual conic. And guess what, this is actually the very same proof I came up with. Great, so what's the problem? Don't you notice that the above proof could basically work for just... ANY Y ???? I didn't use the assumption that Y = P1 at all. Which means that I just "proved" that all projective varieties are normal, which is obviously fucking false. Actually, if you look at theorem 3.2c, the same proof would even work for affines. I just proved that every variety on the planet is normal. So here we are, in a situation similar to the "TCC incident" where I proved something I shouldn't have.
Folks, we might be in the middle of the worst run this blog has had. Let's recap: For 3.13, I had to look up a solution. 3.14: skipped. For 3.15, I could only do half of it and even made amistake while doing so. I've... already said enough about 3.16. And 3.17, as you can tell, is off to a bad start. All with drastic delays in between.
Well, all according to plan, eh? As we all know, "The purpose of this blog is not to get better, but..."