I found my error. It took a long time but I found my error. Everything is fine, I think, up till here:

This is where the ☆*:.｡. magic .｡.:*☆ BS begins. Let's look at equation (1):

0

= hn + c n-1hn-1 + + c 1h + c0

(1)

The error is definitely subtle for an amateur like me. When I "plug in P" into this equation, what exactly am I doing? I'm treating both sides of this equation as functions.

Now, for elements of S = S(Y )_mp, where Y is a variety, this is fine, I think. But what we're looking at here is K(S), the fraction field of S. And we cannot necessarilly treat those elements as functions. the c_i's in that equation are, by assumption, elements of S. But h? We're assuming that h ∈ K(S). In fact, I wrote that h = 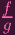∕ 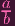. Tell me: Does plugging in P into this equation make sense? Remember how I assumed that a(P) = 0? Well, if you plug in P now (remember I showed, correctly I think, that f(P) = 0), you get 0∕0. Yeah.

So what does the equality in (1) mean? It means that if you cross multiply the elements, they're equal in S, at which point we can treat them like functions. But this cross-multiplication is precisely what I did in an earlier step, to get to equation (2):

0

= (f∕g)n + c n-1(a∕b)(f∕g)n-1 + + c 1(a∕b)n-1(f∕g) + c 0(a∕b)n

(2)

And I already went over what happens when you plug in P in here. In particular: c₀ isn't left isolated, so I can NOT claim that c₀ = 0. THAT'S where my proof breaks down.

The actual proof is "easy". Remember that S(Y ) = k[x,y]. That is integrally closed And the localization S(Y )_mp is also integrally closed . I mean... that is taking those facts for granted, but it's fine....

I knew I had to fix this error before moving on, or else the entire rest of the exercise (and, in fact, the next one as well) would have been screwed.

By the way,

A new week is upon us, let's see how we do.

We're midway through. Let's check the performance meter to see how we're doing:



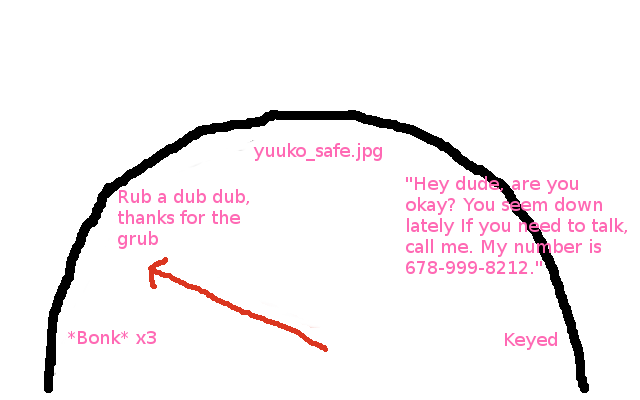
Phew. *Wipes forhead*. Just barely made it out of *Bonk* x3 thanks to this errata. I am still in the sub-rub a dub dub hub, however (give me your strength, commie subs). I'd like my next post to be the rest of the exercise in one swoop, rather than having to split it up into letter-by-letter parts, but we'll see.