I.7.3
9/24/2021

 How now? Will the men make one?
How now? Will the men make one?
 Here, hard by.
Here, hard by.
 Well, how then? Pressed thee what manner of man?
Well, how then? Pressed thee what manner of man?
 Thine eyes shall jure it, my gracious lord. By my troth, all men are marked
commendable in concert with war.
Thine eyes shall jure it, my gracious lord. By my troth, all men are marked
commendable in concert with war.
 A Kendal green for one, buckram for two, yet all's one to cross a beast.
Hither, they come:
A Kendal green for one, buckram for two, yet all's one to cross a beast.
Hither, they come:
 Though my past hath me girded at, the League of Legends then imported
me, then imparted: Nothing's worth, whence thoughts bloody be. Pick no quarrel.
Too willful-blame is the soldier want of government. To undo the knot of the
beast, and put them beside their patience; takes not sword, but word.
Though my past hath me girded at, the League of Legends then imported
me, then imparted: Nothing's worth, whence thoughts bloody be. Pick no quarrel.
Too willful-blame is the soldier want of government. To undo the knot of the
beast, and put them beside their patience; takes not sword, but word.
 I' faith, since my nativity, beasts have quipped at my femininity. But no
more. Thy beast is thy lover. Make a stewed prune and kiss his lips; Play the
Maid Marian against thy spirits. Marry, make them call thee for a reckoning; And
find their woman banish'd from their bed, their own spirits bestirr'd.
I' faith, since my nativity, beasts have quipped at my femininity. But no
more. Thy beast is thy lover. Make a stewed prune and kiss his lips; Play the
Maid Marian against thy spirits. Marry, make them call thee for a reckoning; And
find their woman banish'd from their bed, their own spirits bestirr'd.
 Hark, sounds the Hulk. 'Zounds, make it! Tiger-footed rage, the brawn of
Hercules, mail befitting of Mars; 'Sblood, spirit, keep thee in a fit of bloody rage!
A' would hulk upon hulk, fortune favors bulk.
Hark, sounds the Hulk. 'Zounds, make it! Tiger-footed rage, the brawn of
Hercules, mail befitting of Mars; 'Sblood, spirit, keep thee in a fit of bloody rage!
A' would hulk upon hulk, fortune favors bulk.
 What now? Prithee, I am earless. Perforce, no devil could cozen an audile
eunuch. Nor could Rumor, with painted tongues uncounted, stick one in a closed
vent. What do motions of the mouth speak, but excellent Welsh? For
a tongue with no ear is a case want its pistol; A sheath: sword stolen.
What now? Prithee, I am earless. Perforce, no devil could cozen an audile
eunuch. Nor could Rumor, with painted tongues uncounted, stick one in a closed
vent. What do motions of the mouth speak, but excellent Welsh? For
a tongue with no ear is a case want its pistol; A sheath: sword stolen.

The King.

The Hotspur.

The Harlot.

The Bastard.

The Eunuch.

The Logi.

The Cuckold.

Okay, now that that's over, we can start on the math. Glad to have that out of
my system.

SOOOOO, wuts happenin in this exercise? given P ∈ Y nonsingular, I need to
construct its unique "tangent line" L = TP(Y ) so here's the definition of
intersection multiplicity:

AND, the definition of multiplicity:

Take that all in, reader. Got it? Understood? Alright then. What we're going to
do now is just fucking ignore it all lol. Hark: Listen: I'm not good at abstract algebra, so when
you ask me to deal with the "length of the Sp module", I'm going to struggle.
HOWEVER, it's pretty obvious what the line should be intuitively, because, you
know, it's called a tangent line:
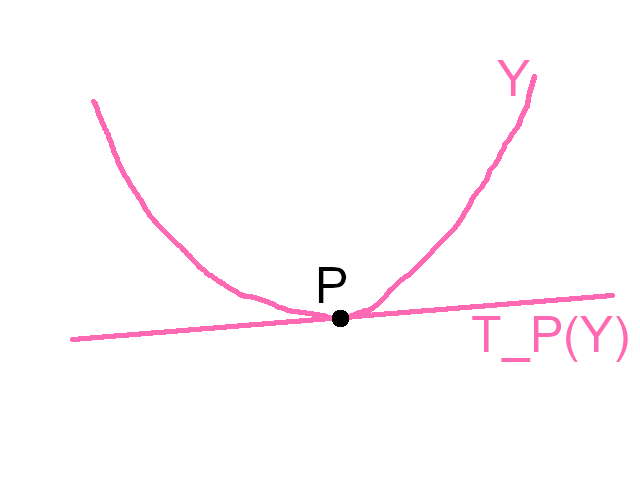
Soooo... we're looking for matching gradient vectors. YEP. JUST GOOD OLD
CALC INTUITION FUCK THE "LENGTH OF MODULES" BS. (if you
needed any more intuition: Note how the "intersection multiplicity" is
"greater than 1" because the line is coinciding with the curve instead of
crossing it. The multiplicity in my pic would prolly be 2, cause it looks
locally quadratic) Ok. Let Y = Z(f). Then we want the gradient of f at
P
| ∇f(P) | =
![[∂f ∂f ∂f ]
∂x-(P ) ∂y-(P ) ∂z(P )](Ip7p30x.png) |
to match the gradient of L = Z(g) = Z(ax + by + cz) at P:
| ∇g(P) | =
![[a b c]](Ip7p31x.png) |
which straight up just forces a =
 (P) etc. SO THERE'S YOUR
TANGENT LINE. Oh, and we did use the nonsingularity assumption (the
gradient of f is nonzero, so (a,b,c) is a proper projective point. Hence, our map
is simply
(P) etc. SO THERE'S YOUR
TANGENT LINE. Oh, and we did use the nonsingularity assumption (the
gradient of f is nonzero, so (a,b,c) is a proper projective point. Hence, our map
is simply
| ϕ : RegY | → (P2)* | ||
| P |
 ∇f(P) ∇f(P) | ||
= (
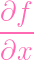 (P), (P),
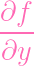 (P), (P),
 (P)) (P)) |
Lol, nice. Now I have to show that it's a morphism. And, well.. each
component here is a homogenous polynomial and I think that's BASICALLY
good enough... I THINK. YEAH.
Also Tails Gets Trolled is unironically good.