I.7.2d
9/21/2021

I have learned that Murid and I apparently share a fear/hatred of forms and
applications, and that has convinced me to republish a VERY OLD post on this
site. Application haters, this one's 4 you:
(I made very minor edits–mostly cutting).
TOPICAL, as I am currently still unemployed (accidentally), and it's about time
that I start lookin for jobs. But, fuck (Buttfuck) I don't even know what kind of
job I should be looking for. You know what? It's time to get my shit together.
I'm tired of sitting around like some kind of fucking pussy, like some
kind of slob, instead of making concrete progress. Fuck negativity. Fuck
pessimism. Let's do things. Let's get things done. Let's try to fucking
win for once. I don't want to hear any more complaining, and whining,
or any of that weak ass shit. I don't want no more negativity. I don't
want any depressive fucks around me (*instantly loses every neocities
follower). It's time for positive energy. Positive vibes only. It's time to
start putting my effort into something that will matter, something that
will last, something that will make a difference. If you want things to
change, you actually have to take action towards it. So you know what? I've
had it. I've fucking had it. I'm getting discplined I'm going to make a
schedule. I'm going to block out time. I'm going to stop improvising. I'm
going to have a plan. No more fucking around, motherfuckers.. That's
right. It's time. It's time to procrastinate by doing useless math lololololo
D

Err, yea, sry for the delay. I got very confused while trying to wrap up this ex and the next. BUT HERE I AM.
OK, just like last time, we'll need prop 7.6 and it's proof:
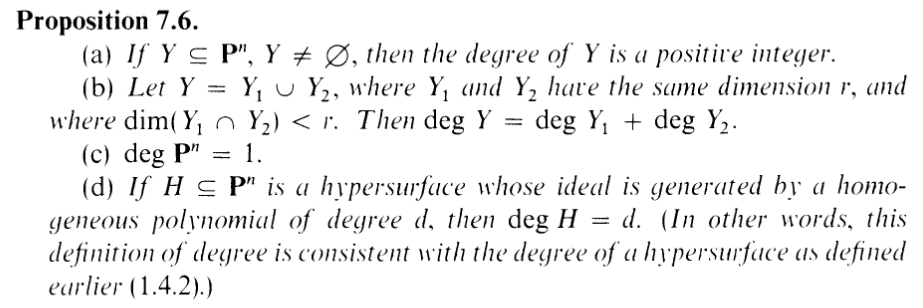

Here's 2.17. Main point, letting I1 = (f), I2 = (g), we can think of Y as Z(I1) ∩ Z(I2) = Z(I1 + I2) = Z(f,g)
This time we, again, default to the prop 7.6 proof, and we use this fancy SHORT EXACT SEQUENCE
 |
TBH, I don't actually understand what is going on in the proof in this part, but THAT DON'T MATTER FOR ME. What I care about is this
additive propertyof Hilbert polynomials:| PS∕I1⊕S∕I2 | = PS∕(I1∩I2) + PS∕(I1+I2) |
i.e.
| PS∕(I1+I2) | = PS∕I1⊕S∕I2 - PS∕(I1∩I2) |
I.E.
| PS∕(f,g) | = PS∕(f)⊕S∕(g) - PS∕(fg) |
Annnnnd this is where I had to look at LE SOL. You'll have to forgive me, because I honestly can't figure out what the grading is supposed to be on the direct sum. Listen: The Hilbert polynomial counts the length of the basis for each grade. I do know that a basis for S∕I1 ⊕ S∕I2 is a basis for S∕I1 combined with a basis for S∕I2. Hence dim k(S∕I1 ⊕ S∕I2) = dim k(S∕I1) + dim k(S∕I2). However, this statement is for the whole space. Does it apply for each grade of the module? i.e.
| ∀l : dim k((S∕I1 ⊕ S∕I2)l) | = dim k((S∕I1)l) + dim k((S∕I2)l) | ||
 PS∕I1⊕S∕I2 PS∕I1⊕S∕I2 | = PS∕I1 + PS∕I2 |
I was tempted to conclude this but was unsure about this for a few reasons
(partly cause I didn't know how to grade the direct sum, and partly cause the
proof of 7.6b was kinda confusing me). WELL, the solution confirms that it's true,
soooooo yeah:
| PS∕(f,g) | = PS∕(f) + PS∕(g) - PS∕(fg) | ||
=
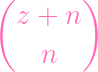 - -
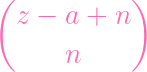 + +
 - -
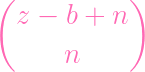 - PS∕(fg) - PS∕(fg) | |||
= 2
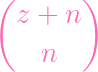 - -
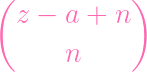 - -
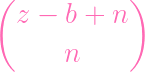 - PS∕(fg) - PS∕(fg) |
soooo, what is PS∕(fg)? You'll have to forgive me again. The solution does
have a little trick here. Look at prop 7.6(d) and its proof again. Now, 7.6d states
its result for hypersurfaces. And hypersurfaces are defined as the zero set of
irreducible polynomials. fg is not irreducible.
However, thhe result appears to hold nonetheless. Can you find anything on
that proof that hinges on irreducibility? I DON'T THINK SO. Hence, noting that
the degree of fg is a + b, I can write
| PS∕(fg) | =
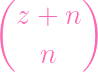 - -
 |
HENCE
| PS∕(f,g) | = 2
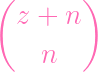 - -
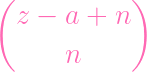 - -
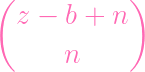 - PS∕(fg) - PS∕(fg) | ||
= 2
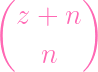 - -
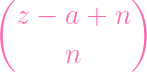 - -
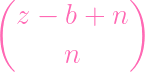 - ( - (
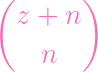 - -
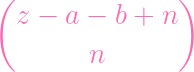 ) ) | |||
= 2
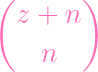 - -
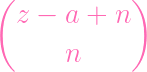 - -
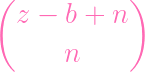 - ( - (
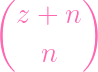 - -
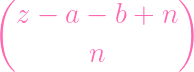 ) ) | |||
=
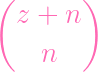 - -
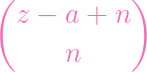 - -
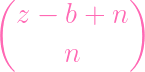 + +
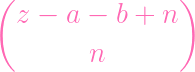 | |||
=
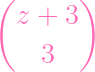 - -
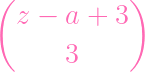 - -
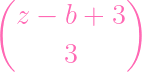 + +
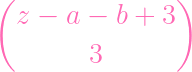 | |||
=
 (z + 3)(z + 2)(z + 1) - (z + 3)(z + 2)(z + 1) -
 (z - a + 3)(z - a + 2)(z - a + 1) - (z - a + 3)(z - a + 2)(z - a + 1) -
 (z - b + 3)(z - b + 2)(z - b + 1) + (z - b + 3)(z - b + 2)(z - b + 1) +
 (z - (a + b) + 3)(z - (a + b) + 2)(z - (a + b) + 1) (z - (a + b) + 3)(z - (a + b) + 2)(z - (a + b) + 1) |
Now plugging in 0,
| PS∕(f,g)(0) | =
 (3)(2)(1) - (3)(2)(1) -
 (-a + 3)(-a + 2)(-a + 1) - (-a + 3)(-a + 2)(-a + 1) -
 (-b + 3)(-b + 2)(-b + 1) + (-b + 3)(-b + 2)(-b + 1) +
 (-(a + b) + 3)(-(a + b) + 2)(-(a + b) + 1) (-(a + b) + 3)(-(a + b) + 2)(-(a + b) + 1) | ||
= 1 -
 ((3 - a)(2 - a)(1 - a) - (3 - b)(2 - b)(1 - b) + (3 - (a + b))(2 - (a + b))(1 - (a + b))) ((3 - a)(2 - a)(1 - a) - (3 - b)(2 - b)(1 - b) + (3 - (a + b))(2 - (a + b))(1 - (a + b))) |
And the rest is just VERY ANNOYING ALGEBRA. IT'S IN MY NOTES.
EXERCISE. LEFT. TO. READER.
Also, part e? According to the solution, that involves the tensor product. And I've
already shown what my reaction to that is.