I.7.4
9/25/2021

Well, Hole, that's quite a feat you've had so far, hm? Not bad, Hole, you're not
bad, but are you good? That is the question I'm asking. Not, "Are you
okay?" or "How are you feeling?" I am not interested in that sort of talk.
You know what I am saying, Hole? That's not the sort of question I am
asking. That's not the sort of thing I want to talk about. What I am
asking is, are you good, skillwise? Skillwise, Hole. I have strings. You
should be one of the heads in the room, you know, Hole? The ones with
sweatpants? You are quite the mind, Hole. I spy potential. I forsee great heights.
I have that sort of eye. I have that sort of power. Do you understand
my question, Hole? Are you good? That is my question. Think it over,
Hole. Please, think it over. Please, please. Please, please, please, please,
please, please, please, ruminate on it. I know you can slice through taut
rope. I know you know your city's streets like a cab driver. I know the
dark matter in your brain is plentiful. I have fucked your brain tissue
before. I have stuck my dick in your ooey gooey dusty goodness. My
penis penetrated the folds–those tight, smooth, taut folds on the so-called
"logical" side, and it reached inside to the dark matter. Men have more dark
matter than women, you know? That is why I prefer to fuck men. That is
why, in case you wanted to know. Goodness, those folds stimulated my
frenulum. They pinched my foreskin such that it almost slipped away.
I wonder if I should have sacrificed my foreskin to the innards of your
mindmatter. I've dreamt for long of how it would be to dog-ear your
brain with many people's foreskin; thousands of foreskin patches, peeking
through the cracks, bulging out, hanging like water balloons. Anyway, that
isn't my point, Hole. My point is this: Can you–Hold, Hole, I'm getting
a call. Yes, madam... Yes, madam... Yes, madam... No, madam.... Yes,
madam.... No, madam.... Yes, madam..... Yes, madam.... Yes, madam...... No,
madam.... No, madam...... Yes, madam.... Yes, madam..... No, madam.... Yes,
madam..... No, madam..... No, madam..... Yes, madam..... Yes, madam....
Yes, madam..... No, madam...... Yes, madam....... No, madam..... Yes,
madam....... No, madam...... Yes, madam........... Sorry about that, that was
my wife. She's taken quite a liking to you, Hole. She really has. Says
she wants to invite you over for dinner some time. She cooks a mean
curry, Hole. A very mean curry, Hole. What do you think, Hole? Are
you up for it? Or are you down? Either way, you are coming. Ha.. Ha...
Ha... Anyway, Hole, back to my main point. Now, what was it that I
was talking about? Ah, yes, thank you for jogging my memory, Hole. I
do need a quick jog here and there, a jab hither and tither, you know
what I am saying, Hole? We all need an up-me-pick to start the day,
Hole. We all need a bit of the back-on-pat-the to hit the ground running,
Hole. A rub-shoulder, you know what I am saying, Hole? The question,
Hole, is not whether or not you are feeling good, but whether you are
capable, Hole. Hole, are you in the zone? Are you present, Hole? I need you
to answer my question, Hole. Where is the arrow pointing Hole? Is it
pointing up? Down? Either way, you are coming. Ha.... Ha..... Ha.......
Ha..... Ha..... Ha...... Ha...... Ha..... Ha....... Ha........ Ha.... Ha..... Ha......
Ha..... Ha........ Ha..... Ha...... Ha...... Ha...... Ha..... Come on, now, Hole.
Maintain the network, Hole. Come on, now, Hole. Come on now, Hole. I'm
fading, Hole. Hole, don't let me fade. What are you doing, Hole. Cut it
out, Hole. Not me, though. Do not cut me out, Hole. Ha... Ha.... Ha....
Ha... Ha... Ha...... Ha..... Ha..... Ha..... Ha...... Ha..... Ha.... Stay with me,
Hole. Stick with me, Hole. Sweet curry, spicy curry. Oh, Hole, we used to
be so good together. Oh, Hole. You were always one of the good ones.
I tell you Hole, you were one of the greats. You have potential, Hole.
You have this under control, Hole. Come on now. Stop it, Hole. Don't
let me fade, Hole. Stay with me, Hole. Hold, Hole. Ha...... Ha..... Ha.....
Ha.... Ha.... Ha...... Ha........ Ha......... Ha......... Ha....... Ha....... Ha.......
Anyway, this exercise is slightly confusing the way it's phrased, but it's pretty
simple once you decode it. Let's start by following the hint. btw: I should have
mentioned this last time, but the best way to think of (P2)* is as a
subset of P2 (with the Zariski topology, which Hartshorne should have
mentioned last time, the fucker). But sometimes we take points in (P2)* and
identify them with lines in P2. So points in (P2)* "stand for" lines in P2.
So what the hint is telling us to do is find all the points that stand for
tangent lines (or pass through singular points). Letting Y = Z(f), let's set
| gx | =
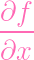 - x - x | ||
| gy | =
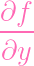 - y - y | ||
| gz | =
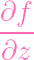 - z - z |
Then the tangent lines (the points that stand for tangent lines) are given by
the closed set Z1 = Z(gx,gy,gz)
Okay so having established that, we'd like to show that the points in (P2)*
whose representative lines intersect S = SingY makes a closed set. Well, I know
that S is closed (it's just the zero set of the partials of f), but those are the
points in Y that are singular, not the lines intersecting Y .................... Fuck this.
I can't figure it out. I'm sorry, I just fucking can't. I'm calling the god damn
motherfucking set Z2 and going with it. Fuck this fucking god damn shit. uck this
I spent so much time and I can't figure it out fucking worthless fuck.
So, I'm just going to set K = Z1 ∪ Z2 which is "obviously" a proper
closed subset. Now, the implication of the hint is that the set U must
be the complement of K in P2. And this makes sense. Taking a point
L ∈ U, think of the line L (ABUSE OF NOTATION) it represents in
P2, then look at the MAIN RESULT of this section, Bezout's theorem:
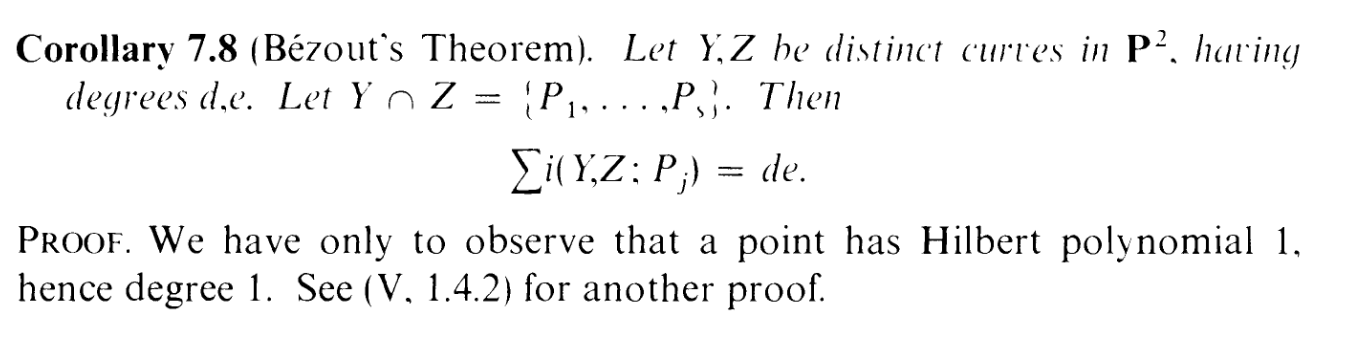
Letting Z = L for this theorem, which has degree 1, we have
| ∑ i(Y,L; Pj) | = d |
Now, without going into too much abstract algebra, it's intuitively clear that
every point of intersection of Y with L has multiplicity exactly 1, because these
are "ordinary" intersections (intersections that aren't tangent, which would have
multiplicity greater than 1 according to last time, and intersections that
don't cross singular points, which thinking about it visually would also
possibly have multiplicity greater than 1). So there must be exactly d terms
in the summation, i.e. there are exactly d points of intersection. Done.
That was a lackluster explanation, lol. Fucking pathetic. SEEYA NEXT TIME.