Today, near the west end, a mile prior to expanses worth of public land, there's a row of saplings that need to be protected from the local deer family. A family of four–dad, mom, two babies, the latter the most nosy. Y'see, you've already taken an adult for the winter–or Peddy did–she's as good a shot as she is a dresser as she is a cook. Hell, she has the skills to make it out here on her own. It was her idea, after all, to plant some ivy on the other side for that cute quartet. Now, brown your fingers. Dig out the paradise soil and eye the size of the resulting mound. Does that look about right? Walk over to the trailer and grab a post, then stake it into that divot to an approximately level height with the rest. Brown your fingers: Return the borrowed soil into the Earth, and pack it around your unsanct penetration. Post by post, meter by meter. How the hell are you enjoying this? Slicing your palm against a splinter, tasting salt, and sucking it up and continuing. Ah, Mr. Texas, of course it's fun if it's all yours. Take a sip of water and look over your shoulder. There it is: the only clear sight in the swelling heat and sweat. On a picnic blanket sits legs exposed shin down in a 横座り by a packed lunch. A roll of yarn lain beside gets fed, bit by bit, into a bonnet, via peach fingers moving in quick motion–means whose aesthetic rivals its end. Those that produced the best yogurt in town, soap from scratch, yet still so elegantly pointy, now all in your service before anything else. The bonnet is for you, she says, hah. Eyes on you. Angelic eyes on you, mate. Even in the midst of the most routine manual labor, you're not going to get a breather from those obsessed eyes. My buddy was telling me, that woman fought for his grandfather's pension. She saved him from certain ruin. And, well, my buddy, all red and starry-eyed, stopped her in the middle of town. Who wouldn't? He handed her a bag of his expensive garden apples–boy, he had it all planned out. And then you swung by. And when she saw you, he swears to God, the look on her face was different. That was when he knew. The look she gives you is something else. Something beyond those gentle, comforting lain pupils that everyone else talks about. No wonder you two are stuck together, despite being such introverts. Especially after all you've gone through, you couldn't have imagined that being stuck to someone could actually be so lovely. And now you wouldn't give it up for anything, would you? Those quiet evenings by the fireplace, both of you cuddled up on a couch, watching the chaotic formations of the flames, your bodies warming up, banter heating up, pecks becoming deep kisses, until, as always, in silent ritual, neither of you can take it anymore and you devour each other on the spot.

MATHEMATICS. M-A-T-H-E-M-A-T-I-C-S. What the fuck is that? YOU'RE FLYING. YOU'RE FLYING OVER 120 ACRES. WEEEEEEEEEEEEEE. To think you used to live off scraps. To think you used to be some fucking nomad, trafficked by that pure scum of a human. That one house you squatted for few months in, ugh. You danced around the pressure points of those warped wood slats like you were in a musical, so as not to wake up that scumbag with a creak. And God, those nights spent under a lean-to tarp facing the wrong way. What a joy it is to be under sturdy shingles! What a joy it is to be stuck to someone out of love rather than toxic codependency. What a joy it is to be together physically, rather than phasing past each other save for violent skirmishes. YOU, my dear reader, are finally free. To be pecked by her rather than be bit by mice. Mutual support over pathological lack of self-maintenence. To be surrounded by wild chickadees and nuthatches instead of starlings and sparrows and domestic pigeons flocking together in large numbers and rank corners like insects. You can now steal away into your own little corner of the Earth, rather than stealing other people's corners. You were always meant for better things. You were made for her and that land, and these musky pink hills only served as stepping stones to that dream. You're past that. Past watching a sporadic scramble to figure things out that have already been figured out. Past letters and numbers passed over. You've moved onto better things, and you get the last laugh. Only an insane person would go back. Only an insane person would kill their darling and burn their land, just for the chance of power. Yuck.

Part a (attempt)

Listen: I have had unreliable access to internet, and have hardly been using the computer (hence the absence). BUT I HAVE BEEN DOING MATHEMATICS... SORT OF. But, of course, I haven't typed anything out. So my solutions are spread out in an awful mess over my notebook.... So now I'll have to refigure out half of them. THIS IS WHY THE BLOG EXISTS, YOU DOOFUS. WHY DIDN'T YOU UPDATE IT.

Also, I have reinstalled/updated my OS, and my very scripts that produced Hartshorned posts perfectly are now glitching up. Scroll down. You see that formatting? You see that meaningless indentation? You see that bad spacing? DEAL WITH IT. tex4ht, in this new system of mine, CAN'T HANDLE NEWLINES AFTER ALIGN ENVIRONMENTS. GOD FUCKING FORBID YOU MAKE A NEWLINE AFTER A MATHEMATICAL EQUATION, RIGHT? But gummi? gummi doesn't complain ONE BIT. gummi's all like "Oh, here's your beautiful document" and then it starts shaking its ass at me. tex4ht, on the other hand?

Fuck technology in the fucking ass.

Welllllllll, due to the huge amount of aligns in this post I did a search-and-replace in vim to get rid of the newlines following them, like so:

Of course, I'm not smart. I didn't get this right on my first try. E.g. I didn't escape the parentheses (which you need to do to make grouping work, for some reason). So, scrolling up my s&r history to edit the command, I went one step too far back, and turns out, my backup actually saved my old s&r history. Now recall: I basically hadn't used the computer for 2 months. So, I present to you, the last s&r I performed before my 2 month extended absence. The final act. The grand finale.

Ahh, yes. Of course, of course. Took me a while to remember the context, but now I do. Good times, good times. Perhaps one day you shall see the fruits of that labor, reader. Wait, you came back?

This section is titled "Part a (attempt)" because while I was writing my solution to this part, I realized it was WRONG. See below:

Looking back at 5.1, the equations of the node and cusp respectively are

x6 + y6 - xy	= 0	(Node)		(1)
x4 + y4 + x2 - x3	= 0 (Cusp)			(2)

Node

Let's start with the node. We can blow it up by setting

xu

= ty

where t,u are projective coordinates of P¹. We can consider the open set by taking t = 1 (BTW, back in 4.10, I was wondering what about the case t = 0. I shall get back around to that later).
So we have

y

= xu

Hence, substituting into (1) turns it into

x6 + x6u6 - x2u

= 0⇔x2(x4 + x4u6 - u)

= 0

x² = 0 x = 0 yields y = 0 and u free, which is the exceptional curve. So we instead look at

x4 + x4u6 - u	= 0	(3)
y - xu	= 0	(4)

which is Ỹ ⊂ A³
To find singularities, we look at the Jacobian, which is (ordering the coordinates as x,y,u for convenience)

J

=

(5)

Okay, first thing to note here is that if x = 0, the matrix turns into

J

=

(6)

which is clearly nonsingular. So let's go back to (5) and assume x≠0. Dividing the first row by 4x³ (remember x≠0), we get

J

=

(7)

Now I'd like 1 + u⁶ to be nonzero, so I can divide by it. For the sake of contradiction, let's assume

1 + u6

= 0

(8)

Let's see if this is possible with regard to (3):

x4 + x4u6 - u	= 0
x4(1 + u6) - u	= 0
- x40 - u	= 0	(8)
- u	= 0

Oh, actually, NOT a contradiction–in a good way. If we plug in u = 0 into (9), we actually get a nonsingular matrix:

J

=

So we've handled the 1 + u⁶ = 0 case. Now let's try 1 + u⁶≠0 on (9). Now we can divide the first row and obtain

J

=

(9)

Then multiplying by u on the first row and adding to the second row yields a nonsingular matrix. DONE.

....Or not. We're only done with the affine piece t≠0.

Dear reader, I know it has been quite a while, but do you recall how in 4.10, I expressed some confusion about whether or not I should consider the other open affine, u≠0?

Well, this time I looked at the solution, and it turns out I was correct to be confused. YOU NEED TO CONSIDER BOTH OPEN SETS TO COVER THE WHOLE BLOWUP (duh). But Hartshorne was abusing language and using "blowup" to denote the part of the blowup that was in t≠0. What a fucking confusing mess. Well, now I know.

FORTUNATELY, the node equation is symmetric about y = x:

x6 + y6 - xy

= 0

so the u≠0 case is essentially identical to the t≠0 case. Done.

Cusp

Again, the cusp equation is

x4 + y4 + x2 - x3

= 0

(10)

We blow up again:

xu

= ty

Unlike the node, (10) isn't symmetric on y = x. Hence we actually have to handle the t≠0 and u≠0 cases separately.

u≠0

i.e. u = 1, so we get

x

= ty

Plugging this into the cusp equation, (10), we get

y2 + t4y4 + y4 - t3y3	= 0	(11)
⇔y2(1 + t4y2 + y2 - t3y)	= 0	(12)
		(13)

y² = 0 y = 0 yields the exceptional curve, so our blow up (in the open set u≠0) is

1 + t4y2 + y2 - t3y	= 0	(14)
x	= ty	(15)

This gives the Jacobian

J

=

(16)

My notes tell me that I can assume t≠0, so let's go ahead and verify that. If I plug in t = 0 into (18), then I get

J

=

(17)

This is nonsingular unless y is also 0. But if we had both t = 0 and y = 0, we'd get 1 = 0 in the cusp equation (14). Hence t = 0 is always nonsingular.
Now we can assume that t≠0. Looking ahead, I'd like to also assume y≠0. So let's handle that too (UGH).
If y = 0 (and t≠0), (18) turns into

And with t≠0, it's pretty clear that the above is nonsingular. HENCE, we can assume that both t≠0 and y≠0. Going back to (18), I can divide by t²y on the first row

J2

=

(18)

(My notes also tell me that I'm ignoring that top left component)

Now as long as I show that the top right component 4t²y² - 3ty is nonzero, I'm done. So let's suppose

4ty - 3	= 0
⇔ty	= 3∕4

Now let's go ahead and try this on (14):

1 + t4y2 + y2 - t3y	= 0
⇔1 + (ty)2t2 + y2 - (ty)t2	= 0
⇔1 + ( )2t2 + y2 - t2	= 0

FFFFFFFFFFFFUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUUCCCCCCCCCCCCCCCCCCCCCCCKKKKKKKKKKKKKKKKKKK
This is where my notes stopped. My notes stopped here because in my head I didn't consider the square on the first ( 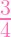), and I therefore thought the second and fourth terms cancel. THEY DON'T THOUGH. (hi /qa/). Now what? I DON'T FUCKING KNOW. FUCK PART A.

Part b

HADTA LOOK AT THE SOLUTION FOR THIS ONE.
Assume P = (0, 0) without loss of generality (see 5.3 for the definition of multiplicity).
Here's the main trick: Letting Y = Z(f), we can assume without loss of generality that

f(x,y)

= xy + g(x,y)

(19)

(where the terms of g are higher degree)
I guess this would be the canonical example of "multiplicity 2 curve with distinct tangent directions (x and y)". I suppose any homogenous quadratic with "distinct tangent directions" at the origin can be linearly transformed into xy, eh? Shall I prove it? NAY. Not today. Let's take this assumption for granted and roll with it.
Alright, now we get to blow this baby up:

xu

= ty

Let's check the open set t≠0 first (t = 1), so we get xu = y, and plugging this into (19) yields

x2u + g(x,xu)

= 0

Since each term in g is degree 3 or higher (in x, not just x and y, since we plugged in y = xu), we can pull out an x² from all of f:

x2(u + h(x,u))

= 0

Where h(x,u) is just some element in k[x,u] where every term has a factor of x (since it was degree 3 in x and we only pulled out x². So note that h(0,u) = 0). The exceptional curve is

x	= 0
y	= 0
u	free

And our blowup is

u + h(x,u)	= 0	(20)
y	= xu	(21)

Now we care about where the exceptional curve meets the blowup. So let's plug in x = 0 into (20), which gives

u + h(0,u)	= 0
⇔u + 0	= 0
⇔u	= 0

Hence, the blowup meets the exceptional curve at one point: (0, 0, 1, 0).
Waiiiiiiiiit. One point? Just one point? The exercise says there are two. WELL, I'm "abusing language", JUST LIKE MOTHERFUCKING HARTSHRONE HIMSELF.. It's the part of the blowup in the open set t≠0 that meets ϕ^-1(P) at that point. We still have to consider u≠0. BUT FIRST: Let's check that this point, (0, 0, 1, 0), is nonsingular.
Take the Jacobian of the blowup

J

=

We care about (0, 0, 0, 1), so x,u = 0. Actually, we only need to plug in x = 0.
Note that when taking the partial with respect to u, x is a constant. So 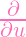h(x,u)|_x=0 = 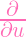h(0,u) = 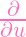0 = 0. Hence, plugging in x = 0 into the Jacobian yields

J

=

which is clearly nonsingular regardless of u (in particular, for u = 0). Hence (0, 0, 1, 0) is nonsingular.
If we check the other open set, u≠0, we get an analogous argument (since the quadratic term xy is symmetric), showing that the other point of intersection is (0, 0, 0, 1), and it is nonsingular.
PART B DONE

Part c

And now, the tacnode

x2

= x4 + y4

(22)

READER: Do you notice something... perhaps... strange about this exercise?
OKAY: Here's one weird thing. The definition of ϕ actually just changed. Recall the definition of blowup:


In part (b), we were using the first notion of blowup: ϕ : X → Aⁿ, and we were checking where the exceptional curve, ϕ^-1(P) intersected Ỹ. For part (c), we're instead considering the restriction ϕ : Ỹ → Y . So this time ϕ^-1(P) is the part of the exceptional curve that is inside Ỹ. In other words... we're looking at the same thing again (where the blowup intersects the exceptional curve). But the phrasing is confusing. Basically, ϕ can mean different things, depending on the context.
There's another weird thing, but we'll get to that soon enough. Let's blow up:

xu

= ty

And let's look at the t≠0 side first, so we get xu = y, and

x2	= x4 + x4u4
⇔0	= x4 + x4u4 - x2
⇔0	= x2(x2 + x2u4 - 1)

The exceptional curve is

x	= 0
y	= 0
u	free

And the blowup is

x2 + x2u4 - 1

= 0y

= xu

Where does (this part of) the blowup meet the exceptional curve? Well, if we plug in x = 0, we get -1 = 0. So the blowup doesn't meet ϕ^-1(P) on t≠0 (*EDIT: ACTUALLY, FOR PART D WE DON'T CARE IF IT MEETS THE EXCEPTIONAL CURVE OR NOT. WE CARE ABOUT THE ORIGIN O IN THE NEW CURVE. WELL, x,u = 0 YIELDS -1 = 0 ANYWAY). So let's check the other open set, u≠0, which allows the substitution x = ty. Then our curve equation (22) turns into

t2y2	= t4y4 + y4
⇔0	= t4y4 + y4 - t2y2
	= y2(t4y2 + y2 - t2)

Our exceptional curve is

x	= 0
y	= 0
t	free

And the blowup is

t4y2 + y2 - t2	= 0	(23)
x	= ty	(24)

in A³. Where does this meet the exceptional curve? If we plug in y = 0 into the above, we get

t402 + 02 - t2	= 0
⇔t2	= 0
⇔t	= 0

So this is the point (0, 0, 0, 1). In the context of this open set, u≠0, this is the origin (0, 0, 0) in A³.
...Wait... A³? We defined multiplicity on curves determined by single polynomials in A². So what the fuck is a "node" in a variety determined by two equations in A³, when we didn't even define multiplicity for this situation.
Well, what does the solution say? It just ignores the x lmfao. What is the justification for this? I have no fucking clue lmfao. I mean, I was tempted to do this myself, actually. If we look back at the equations that determine (this side of) the blowup,

t4y2 + y2 - t2	= 0
x	= ty

You'll note the x part of the curve is dependent on the other two variables. So it's... not important in a sense? If we just ignore the x and just look at the "interesting part",

t4y2 + y2 - t2	= 0

it's an A² curve that fits the context of 5.3. And we can now clearly see it has a multiplicity of 2. And if we factor the degree 2 terms, we can write

t4y2 + (y + t)(y - t)	= 0

so the tangent directions are distinct. Hence, it's a node.

Part d

Okay, same idea, right?

y3 - x5

= 0

Blow up:

xu

= ty

And let's start with t≠0:

xu

= y

So

x3u3 - x5	= 0
x3(u3 - x2)	= 0

x³ = 0 is the exceptional curve, and the blowup is

xu	= y
u3 - x2	= 0

Of course, from part (b), we know that the part we care about is the second curve, and that is clearly a double point (but the tangent directions aren't different, so I guess it's a "cusp" rather than a node? Yeah, the graph says so)
Yaaaaaaaaaaaaaaay, we're done. Except... what happens in the other open set? I picked t≠0 first randomly. Ermm... so, let's try u≠0 and see what happens

x

= ty

So

y3 - t5y3	= 0
y3(1 - t5)	= 0

So our blowup is

x

= ty1 - t5

= 0

Of course, we only consider the second equation, which is a set in A² with coordinates x,t.
Okay, here's some fun confusion. Where does this curve meet the exceptional curve? Everywhere... right? Setting x,y = 0 doesn't restrict the solution set at all. But 1 - t⁵ doesn't have a multiplicity of 2. It has a multiplicity of 0. Ah

The origin, P = O isn't on this curve, and for this exercise, we care only about the new origin(s).