I.5.2
6/12/2021

[rant redacted. my goodness]
This time
we're looking at hypersurfaces in A3, which have dimension 2. Hence, the
Jacobian matrices of nonsingular points will have rank 3 - 2 = 1. So, again, the
singular points will have rank 0. And since our Jacobians are just gradient
vectors, we just need the components to be 0. I.e. we set all the partial derivatives
(along with the surface equation) equal to 0 and solve, just like last time.
Part a
Our system of equations here is:
| xy2 - x2 | = 0 | ||
| y2 | = 0 | ||
| 2xy | = 0 | ||
| - 2z | = 0 |
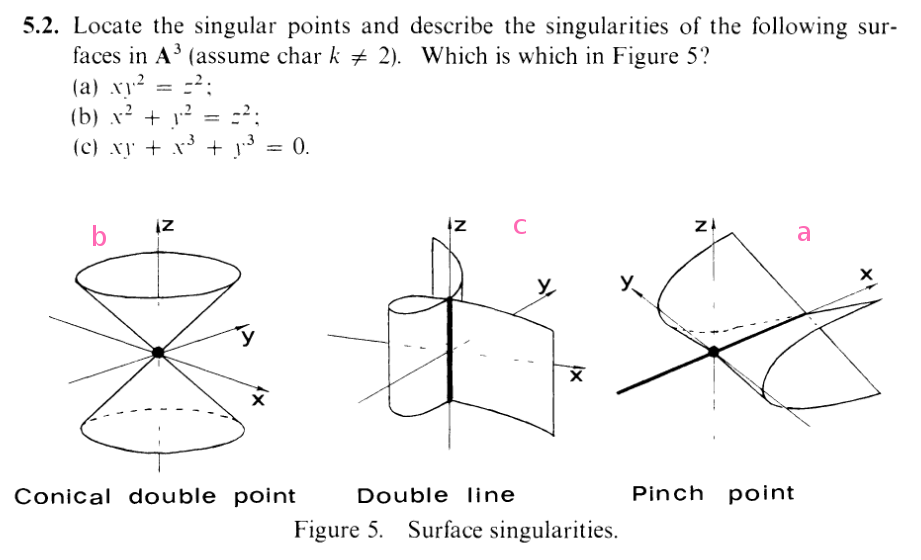
The second and fourth equations imply that y = 0 and z = 0. Plugging these into equations 1 and 3, we see that x can be free. So the singular points are the x-axis. Out of our Queen's figures, it's clearly the "Pinch point".
Part b
Our system of equations here is:
| x2 + y2 - z2 | = 0 | ||
| 2x | = 0 | ||
| 2y | = 0 | ||
| - 2z | = 0 |
I.e. we need x,y,z = 0. So the singular point is (0, 0, 0). So this is clearly the "conical double point"
Part c
Our system of equations here is:
| xy + x3 + y3 | = 0 | ||
| y + 3x2 | = 0 | ||
| x + 3y2 | = 0 | ||
Clearly, z is free. Also, if the characteristic of k is 3, then clearly x,y = 0, leaving the z-axis. And if the characteristic isn't 3? Then plugging in the 3rd equation into the 1st, we get
| y + 3(-3y2)2 | = 0 | ||
 y + 27y4 y + 27y4 | = 0 | ||
 y(1 + 27y3) y(1 + 27y3) | = 0 | ||
We get y = 0 or
| 1 + 27y3 | = 0 | ||
 y3 y3 | =
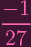 |
Now, watch out: I don't necessarily just want to "cube root" both sides, as there are actually 3 distinct solutions to this equation in an algebraically closed field! I'll leave it written as is (WATCH, reader. Watch how I'm gonna cleverly avoid having to handle all of em). Also, we can get analogous equations for x. So in total our possibilities are x = 0,y = 0,y3 =
 ,x3 =
,x3 =
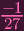 . Now we test these
against the original curve equation
. Now we test these
against the original curve equation | xy + x3 + y3 | = 0 | ||
x = 0,y = 0 obviously works, leaving the z-axis. If only one of them is 0, then the other clearly can't be nonzero, so the only possibility left is y3 =
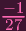 ,x3 =
,x3 =
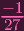 . Plugging these in, we get
. Plugging these in, we get xy +
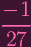 + +
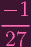 | = 0 | ||
 xy + xy +
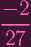 | = 0 | ||
 xy xy | =
 | ||
 x3y3 x3y3 | = (
 )3 )3 | ||
 ( (
 )( )(
 ) ) | =
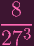 | ||
 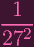 | =
 | ||
 273 273 | = 8 ⋅ 272 | ||
 27 27 | = 8 | ||
 19 19 | = 0 | ||
..............
Okay.... So you know how I said
WATCH, reader. Watch how I'm gonna cleverly avoid having to handle all of em
Errr...... Soo.... as I was typing this out, I realized that 19 = 0 is actually possible if the chark = 19...... cause 19 is a prime number Guys..... It was supposed to be a contradiction...... It was.... supposed to be a contradiction......... Fuck my life..........
Okay, so I got it, phew. Check it out.
| y + 3x2 | = 0 | ||
 xy + 3x3 xy + 3x3 | = 0 | ||
 xy + 3( xy + 3(
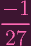 ) ) | = 0 | ||
 xy + xy +
 | = 0 | ||
 xy xy | =
 |
Oooohhh. Now, note how earlier we had
| xy | =
 |
So now we can write
 | =
 | ||
 27 27 | = 18 | ||
 27 27 | = 18 | ||
 9 9 | = 0 |
Which is impossible since we assumed that chark≠3. And thus, we're.... SAFE!

WHEW. It's been a long time since I've used yuuko_safe.jpg, :D
Also, I already "matched" them in the text, but here's the summary: