I.5.10bc
8/22/2021
 BLECCCHHHHHHHHHHHH. You like that? Here, bring your face closer.
BUUAAAAACCCCCCHH. Don't be shy. BLEEEEEEEEEEECCCCCCHHHHHHH.
See? It's not so bad. BLEEEECCCCCCCHHHHHH. BLUEAAAAAAAAAAAACHH.
Once you get used to it, BLUOOOOOOOOOOOOOOOOOOCH, the
smell is actually pretty nice. BWOAAAAAAOOOOCOOOOOOCH.
BWUAAAAAAAAAAAAAAACCCCCHHHHHHHHHH.
BLEEEEOOOOOOOOOOOOOCHHHHHH. It's an acquired taste.
BUOOOOOOOOOOOOOOOOOCH. BLEOOOOOOOOOOOOOOOOOOCH. Sure, I
can do it directly in your mouth. Here, open up. BLEEEEEEEEEEEEECCCCCHHH.
BLUUUUUUUAAAAACCCHH. BLLLLUUUUUUUAACCCCCHHHHH.
How does that taste? Oh, your mouth is full, so I guess you can't answer.
Well, this ain't awkward at all, hahaha. You look like you're having fun.
"BLLLLLLEEEEEEEECCHHH" Oh, look, now you're puking as well. Hell yeah,
join the party. Here, do it in my mouth. "BLEEEEEEEEEEEEEEEEECHHHH"
*Gulp, gulp, gulp.* Hmmmmm, not bad, not bad at all. *Slurp*. Yours has a thicker
texture and a more... salty taste? I can't put my finger on it, it's just different. It's
just so... you. I'm sorry, I'm just so bad at descriptions, haha, that's the best I
could come up with. But I love it. You're awesome. You're fucking awesome, man.
BLUUUUUUUAAAAACH. I know we just met, but I think we have a connection
already. BLEEEEEACCCHHHH. No, you're fucking boss. Want more? Only if
you're comfortable with it. Here BLEEEEEEEEACCCCHHHHH. Now do it on
me again. "BLUAAAAAAAAAAAAACH" *Gulp, gulp, gulp* Pah! Yummy
yum yum in my tummy tum tum. Man, this is getting addicting. My
turn. BLEEEEEEEEEEEEECHHH. BLOOOOOOUUUUCH. Now your
turn. "BLEEEEEEEEEEEEECH" *Slurp* Rub a dub dub, thanks for
the grub. See? There's a rhythm to it. Once you get it, you just do it
automatically. It's like salsa dancing. You ever try salsa dancing? I took salsa
dancing classes up in Frisco and it was super fun. I met some awesome
people there. I even met my bandmembers there. Yeah, I have a band.
Actually, you'd really like it. A lot of our repertoire is centered around
antiauthoritarian themes. We haven't played in a while cause of COVID, though.
*Slurp*. Gaahhhhh. Man, even the aftertaste of your puke is just fucking
awesome. BLEEEECCCCCCCCCCHHHHHH. Awwww, you like mine too?
*Chuckles, then pukes again* Well, yeah, I just maintain a very strict
keto diet and, well, BLEEECCCCHHHHHHHHHH, that's all there is to
it. Wbu? Oh, you're doing intermittent fasting? And it still tastes so
good!? No kidding. Seriously? *Punches you in the arm, then pukes on
it* Haha. BLEEEEEEEEEEECCCCCHHHHH. So, what do you do?
BLECCCHHHHHHHHHHHH. You like that? Here, bring your face closer.
BUUAAAAACCCCCCHH. Don't be shy. BLEEEEEEEEEEECCCCCCHHHHHHH.
See? It's not so bad. BLEEEECCCCCCCHHHHHH. BLUEAAAAAAAAAAAACHH.
Once you get used to it, BLUOOOOOOOOOOOOOOOOOOCH, the
smell is actually pretty nice. BWOAAAAAAOOOOCOOOOOOCH.
BWUAAAAAAAAAAAAAAACCCCCHHHHHHHHHH.
BLEEEEOOOOOOOOOOOOOCHHHHHH. It's an acquired taste.
BUOOOOOOOOOOOOOOOOOCH. BLEOOOOOOOOOOOOOOOOOOCH. Sure, I
can do it directly in your mouth. Here, open up. BLEEEEEEEEEEEEECCCCCHHH.
BLUUUUUUUAAAAACCCHH. BLLLLUUUUUUUAACCCCCHHHHH.
How does that taste? Oh, your mouth is full, so I guess you can't answer.
Well, this ain't awkward at all, hahaha. You look like you're having fun.
"BLLLLLLEEEEEEEECCHHH" Oh, look, now you're puking as well. Hell yeah,
join the party. Here, do it in my mouth. "BLEEEEEEEEEEEEEEEEECHHHH"
*Gulp, gulp, gulp.* Hmmmmm, not bad, not bad at all. *Slurp*. Yours has a thicker
texture and a more... salty taste? I can't put my finger on it, it's just different. It's
just so... you. I'm sorry, I'm just so bad at descriptions, haha, that's the best I
could come up with. But I love it. You're awesome. You're fucking awesome, man.
BLUUUUUUUAAAAACH. I know we just met, but I think we have a connection
already. BLEEEEEACCCHHHH. No, you're fucking boss. Want more? Only if
you're comfortable with it. Here BLEEEEEEEEACCCCHHHHH. Now do it on
me again. "BLUAAAAAAAAAAAAACH" *Gulp, gulp, gulp* Pah! Yummy
yum yum in my tummy tum tum. Man, this is getting addicting. My
turn. BLEEEEEEEEEEEEECHHH. BLOOOOOOUUUUCH. Now your
turn. "BLEEEEEEEEEEEEECH" *Slurp* Rub a dub dub, thanks for
the grub. See? There's a rhythm to it. Once you get it, you just do it
automatically. It's like salsa dancing. You ever try salsa dancing? I took salsa
dancing classes up in Frisco and it was super fun. I met some awesome
people there. I even met my bandmembers there. Yeah, I have a band.
Actually, you'd really like it. A lot of our repertoire is centered around
antiauthoritarian themes. We haven't played in a while cause of COVID, though.
*Slurp*. Gaahhhhh. Man, even the aftertaste of your puke is just fucking
awesome. BLEEEECCCCCCCCCCHHHHHH. Awwww, you like mine too?
*Chuckles, then pukes again* Well, yeah, I just maintain a very strict
keto diet and, well, BLEEECCCCHHHHHHHHHH, that's all there is to
it. Wbu? Oh, you're doing intermittent fasting? And it still tastes so
good!? No kidding. Seriously? *Punches you in the arm, then pukes on
it* Haha. BLEEEEEEEEEEECCCCCHHHHH. So, what do you do?
Ah, hi reader. Sorry about that. I was just doing weed with a Silicon Valley
resident. "Yuck! I'd rather watch ゲロ-themed JAV." Hah! You go do that! We'll
stick to Pornhub, sicko.
After studying the cryptic engravings in my notebook, I've concluded
that the month-ago-me could not finish part (a), so I shall skip that.
Funny point: I do remember that when I was working on this exercise, I
wasted a lot of time because I misread the exercise and assumed that
| TP(X) | = 𝔪∕𝔪2 |
WROOOOOOOOOOOOOOOOOOOOOOOONG. It's actually
| TP(X) | = (𝔪∕𝔪2)* |
It's the dual vector space of 𝔪∕𝔪2.
B
Letting Q = ϕ(P), and 𝔪′ be the maximal ideal of Y , We already know
that there is a corresponding k-algebra map (the natural "pullback")
ϕ# :
 Q,Y
Q,Y | →
 P,X P,X |
(Ahhh, the great staple of this blog: Black sheaf symbols). And since these are
local rings, it has to map 𝔪′ to 𝔪. Hence we can actually consider the restriction
| ϕ# : 𝔪′ | → 𝔪 |
Now suppose h ∈ 𝔪′2, so that h = g2 for some g ∈ 𝔪′. Then
| ϕ#(h) | = ϕ#(g2) | ||
| = ϕ#(g)ϕ#(g) | |||
| ∈ 𝔪2 |
hence we can induce a well-defined map
| ϕ#* : 𝔪′∕𝔪′2 | → 𝔪∕𝔪2 |
with k-linearity inherited from ϕ#. Now, you can see why I was very confused
by not considering the dual (because it's a map from a vector space formed from
something associated with Y to something associated with X, rather than vice
versa). Well, this map induces the map of the dual spaces (X to Y ). Dun.
C
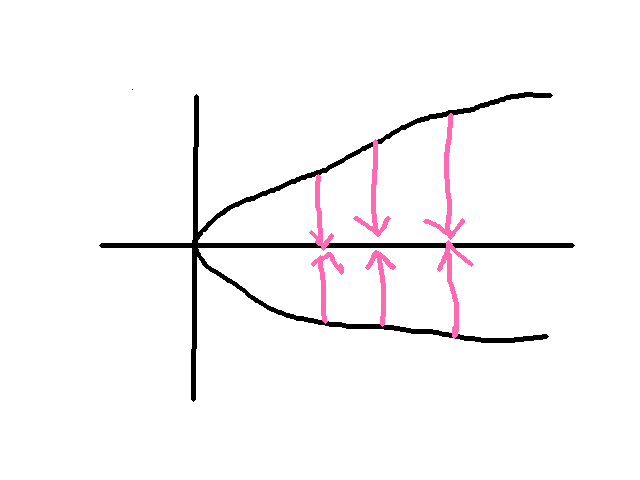
Let
| X | = Z(x - y2) | (the parabola) | ||||
| Y | = Z(x) | (the x-axis) |
so that the projection is
| ϕ : X | → Y | ||
| (y2,y) | → (y2, 0) |
or, you can just think of it as
| (y2,y) | → y2 | ||
| = x |
So you can just think of Y = A1, the affine line. Look, I made a cute picture
of it
Now we consider
| TO(ϕ) : TO(X) | → TO(Y ) |
Reminder: The pullback that induces this is
| δ : 𝔪′∕𝔪′2 | → 𝔪∕𝔪2f |
 f ∘ ϕ f ∘ ϕ |
Here's the key point: Y is actually just the affine line, and its maximal ideal is therefore just (x), so the "f" here is necessarily in the form x ⋅ g(x) for some g ∈ k[x].
| x ⋅ g |
 (x ⋅ g) ∘ ϕ (x ⋅ g) ∘ ϕ |
Let's try plugging in a point into the RHS:
| ((x ⋅ g) ∘ ϕ)(y2,y) | (holy shit this notation is getting cluttered) | ||
| = (x ⋅ g)(y2) | |||
| = y2 ⋅ g(y2) | |||
| = 0 |
The last equality follows from the fact that the maximal ideal 𝔪 is (x,y), so y ∈ 𝔪, which means y2 ∈ 𝔪2, which is hence 0 in 𝔪∕𝔪2. So δ is the 0-map, and hence so is its dual (i.e. TO(ϕ)). Done.