I.5.9
8/20/2021

Break up f into its irreducible components:
| f | = f1
 ft ft |
which likewise breaks Y into its irreducible components:
| Y | = Z(f1) ∪
 ∪ Z(ft) ∪ Z(ft) |
Let P ∈ Z(f1) ∩ Z(f2), and assume without loss of generality that
 (P)≠0 (as given by the condition). Note that, using the product rule,
(P)≠0 (as given by the condition). Note that, using the product rule,
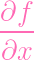 | =
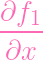 ⋅ f2 ⋅ f2
 ft + ft +
 ⋅ f1 ⋅ f1 | ||
 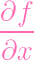 (P) (P) | =
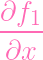 (P) ⋅ f2(P) (P) ⋅ f2(P)
 ft(P) + ft(P) +
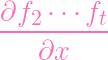 (P) ⋅ f1(P) (P) ⋅ f1(P) | ||
| = 0 | |||
(since f1(P) = 0,f2(P) = 0 |
But this contradicts the nonzeroness of the partial at P. Hence Z(f1) ∩ Z(f2) = ∅. But this contradicts 3.7. Hence Y must only have one irreducible component i.e. Y is irreducible (i.e. f is irreducible). Now that we know Y is a projective variety, we can apply what we learned yesterday ("Paddle Person"... seriously? Fuck my life. I deserve to die). Since the gradient vector (Jacobian) has a nonzero partial derivative at every point, we're dun.