I brought up rational maps last time. A birational map is just an isomorphism in the category of rational maps. I.e.:



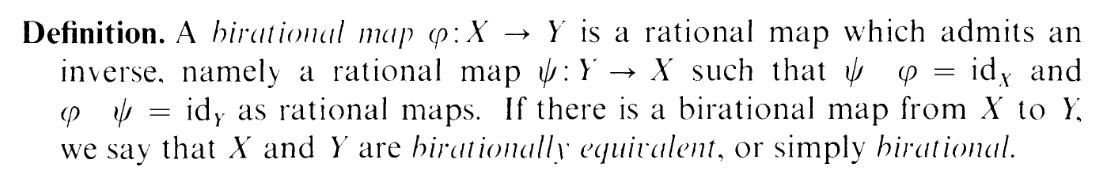
In particular, this exercise mentions 4.5:



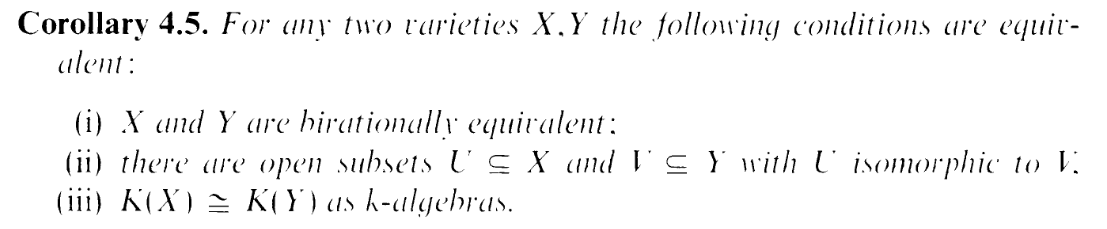
Now: the exercise does make an interesting observation based on condition (iii), but if you're scared of field theory like me, do not fret, for I shall only use fact (ii) in this exercise. I.e. isomorphisms on open sets make birational equivalences

Part a

Trivial thanks to 3.1c, lol.

Part b

Now here's where things get interesting. We have, sitting before us, a cuspoidal cubic. And of course, the highlight of this curve is the cusp in the middle. And what doth our queen say about cusps?



BLOW EM UP, MOTHERFUCKERS.





Errrrr..... What the fucking fuck is going on. Well, at least we know that blow-ups maintain birational equivalence. Let's look at an example. Maybe that will clear things up.





...................................................

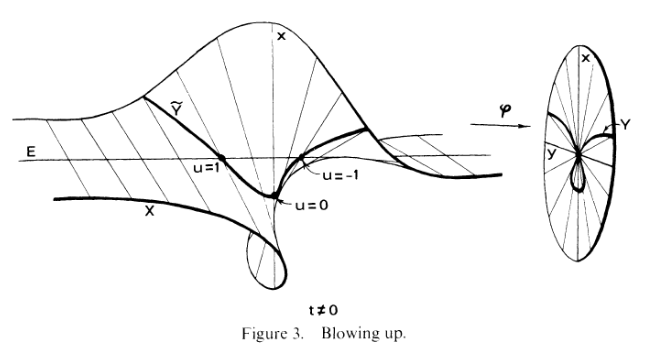
.... Uhhh.... Listen: You know how last time, I said we should loosen up? Let me tell you: That's how we're going to get through this. Pay more attention to the example than the definition. The stuff in the example might seem.... arbitrary. It certainly felt that way to me. So I started Googling it. Yes: Google, unfortunately, because DDG gives atrocious results for math. Now, midway through, I remembered a story I learned, thanks to Koshka, about how a family got raided for looking up info on pressure cookers and backpacks. And then i realized that for the past 10 minutes, I had been furiously typing, straight into the Google botnet, [RANT REDACTED LOL]

So what ended happening is that I switched to DuckDuckGo, and I found this video (y² = x³ even appears as an example!). And from this video I started to see the pattern behind blowing up. Remember what I said about loosening up? The key point here is to not focus on the definition, but the process.

Letting u,t be coordinates for P¹, we consider the variety in A² × P¹ given by

xu	= ty
y2	= x3

Let's set t≠0. Wait, why can we just set t≠0? This was something that confused me about the above examples. But I get it now: t≠0 gives us an open set in the variety, and thanks to corollary 4.5 we can restrict our attention here. In particular, we can turn the projective coordinates u,t just a single affine coordinate u (by setting t = 1), so we can just study

xu	= y
y2	= x3

(So now I guess we're just working in A³) Substituting the first guy into the second, we end up with

x2u2	= x3
x2u2 - x3	= 0
x2(u2 - x)	= 0

So we get x = 0 and u² - x. In the first case, in total, we get x = 0,y = 0, and u arbitrary. However, let's eliminate this case by setting x≠0, which we can do because it gives us an open set. Then we must have x = u² and y = xu. This latter equation can be rewritten as y = u³...

......*Sigh* Do you see it, reader? Do you fucking see what I see? Yes. It's the motherfucking twisted cubic curve. Yaaaay, it came back again -_-. Since the TCC is isomorphic to A¹ (see here), and A¹ is an open set of P¹, we're done.

I did not expect that one of the pieces you get from blowing up the cuspoidal cubic would be a twisted cubic curve. What a fucking weird world we live in, lol

Part c

Oh, it's that exercise that I skipped, haha. Here's 3.14:



Okay, okay, before dealing with Y itself, let's work out this "projection" map:

ϕ : P2 -{P = (0, 0, 1)}	→ P1

Given Q in the domain, I need ϕ(Q) to be "the intersection of the line containing P and Q with z = 0 (which is P¹)". Err okay, let's say that Q = (Q₀,Q₁,Q₂), and let's restrict the domain to be z≠0 (which we can do, cause we only care about birational equivalence). Then we can assume without loss of generality that Q₂ = 1. Now let's parametrically write down the line containing P and Q:

L(t)	= (Q - P)t
t	∈ k

broken up into components, this is

L0	= (Q0 - 0)t
L1	= (Q1 - 0)t
L2	= (1 - 1)t

i.e.

L0	= Q0t
L1	= Q1t
L2	= 0

Hence, seeing z≠0 as A², we can define ϕ on it as

(Q0,Q1)

(Q0,Q1)

Now, this is clearly a morphism but note that this is not the identity map, as the image is in P¹. The map is definitly surjective, but it's not injective, because (kQ₀,kQ₁) maps to the same point as (Q₀,Q₁). However, this is the only case that two points map to the same one. Now we can bring in Y . You see, in z≠0 i.e. A², the equation defining Y just turns into

y2

= x2(x + 1)

And although at first I did some messy algebra, I realize now that the key point is simply that this polynomial aint homogenous, therefore it's infeasible that (kQ₀,kQ₁) and (Q₀,Q₁) are both going to satisfy it. Hence, we've constructed an isomorphism from an open set of Y to P¹, making them birationally equivalent. Done!