From part (c):

I'm an idiot. Yes, the map was injective, but I forgot to take into account that once I restrict the domain, I'm also restricting the image. FUCKING DUH. Once I set z≠0, the map fails to be surjective. So it's not an isomorphism.

(BTW: I caught this error by glancing back at 3.1e. If it were that open set of Y were isomorphic to P¹, then it would be a singleton, lol)

What you're actually supposed to do becomes clear upon graphing it:



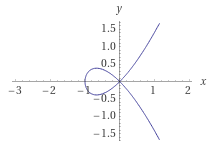
There's a singularity in the middle, so of course we should blow it up, like in part (b). Using coordinates u,t for P¹ and setting t = 1, we get

xu	= y
y2	= x2(x + 1)

Subbing the first equation into the second yields...

x2u2	= x2(x + 1)
⇐⇒x2u2 - x2(x + 1)	= 0
⇐⇒x2(u2 - (x + 1))	= 0
⇐⇒x2(u2 - (x + 1))	= 0

Using the open set x≠0, we can ignore x² = 0, so we end up with

xu	= y
x	= u2 - 1

i.e. it's the curve given by (u,u² - 1,u³ -u) (in the open set where the second coordinate is nonzero). This is clearly isomorphic to the twisted cubic curve. The map

(u,u2 - 1,u3 - u)

(u,u2,u3)

is bijective onto the TCC, and it and its inverse maps are morphisms thanks to this:



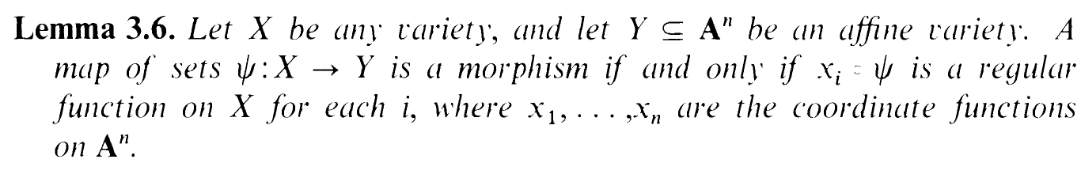
So Y is birational to the TCC, and the TCC itself is birational to P¹, so we're done.

Also, welcome to June! I think June is a pretty cute name, tbh.