I.3.4
4-8-2021
"WTF ARE YOU DOING, YOU MONSTER. WHY WOULD YOU DO THIS? WHY WOULD YOU SKIP
EXERCISES?" Calm down, reader. All I did was look ahead and notice that doing this exercise first would be
helpful for 3.1(c). We'll hop right back there after this. No panic, no panic. I have this under control. Your trusty,
reliable admin knows what he is doing. Of course! I'm always striving to be a dependable person. Someone whose loved
ones can count on in a time of need. You see, putting others above oneself is how great communities are made. Going through life, you'll find that if you're kind, people will be kind back to you. But it's not about getting what you want, it's about helping. The feeling of helping someone is the greatest feeling in the world. People are
happiest when they help other people. So, my suggestion? Don't get too wrapped up in your own problems. Take some time to think about other people. How are they suffering? How can you help? Remember, the world is not all about you. There are other people out there. They're hurting. Think about what you can do for them. If we all help each other, act more kind to each other, we can surely make it. Huh? What's that? Wtf? "Narcissist" is written on my lips with some pinkish substance? Errr,
that's not good. Maybe you should kiss me to make it go away. Make sure to use lots of saliva.
Okay, let's get to the exercise. Remember 2.12? ...Looking back, I'm seeing some fun typos, including
the symbol ρ magically switching to ϕ midway through (... srsly, I really like writing and typing ϕ
so I gravitate towards it). On the other hand, thank fucking goodness I maintain this fucking blog.
Coincidentally, I actually talked about this at the end of that exercise (*blows kiss*), but honestly
doing this exercise would have been horrific had I had to rely on leafing through my messy notes.
I'm going to be assuming familiarity with 2.12 moving forward. Back in that exercise, we had defined the d-uple
embedding
| ρ : Pn | → PN | ||
| (…,xi,…) |
 (…,Mi(x),…) (…,Mi(x),…) |
We showed that ρ induced a homeomorphism Pn ≃ Z(α), which in fact corresponded to the map of coordinate rings
| θ : k[y0,…,yN] | → k[x0,…,xn] | ||
| yi |
 Mi Mi |
(correspondingly inducing k[y0,…,yN]∕α ≃ k[x0,…,xn])
Remember: Unless our varieties are affine, we can't assume that isomorphic coordinate rings give us isomorphic varieties. Otherwise this exercise would be trivial. We have to show manually that ρ and its inverse satisfies the regularity properties.
Let's start with ρ. Give me some V open in Z(α), and f : V → k regular. I need to show that f ∘ ρ : ρ-1(V ) → k is regular.
Given Y ∈ V , we know that there is some U open in V containing Y such that f = g∕h on U (g,h ∈ k[y0,…,yN], h nowhere zero on U). ← btw, everytime I have to do this regular thing, I have to write out this crazy long setup. So annoying. You might see me shorten or omit some of it in the future..... perhaps in this very exercise!
Given X ∈ ρ-1(U), note that
| f ∘ ρ(X) | = f(ρ(X)) | ||
=
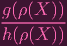 | |||
=
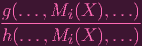 | |||
=
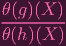 | |||
And note that for θ(h)(X) = 0
 h(ρ(X)) = 0, which is a contradiction since
X ∈ ρ-1(U)
h(ρ(X)) = 0, which is a contradiction since
X ∈ ρ-1(U)
 ρ(X) ∈ U
ρ(X) ∈ U
 h(ρ(X))≠0, so θ(h) is nowhere zero on ρ-1(U), and f ∘ρ = θ(g)∕θ(h) on
ρ-1(U).
h(ρ(X))≠0, so θ(h) is nowhere zero on ρ-1(U), and f ∘ρ = θ(g)∕θ(h) on
ρ-1(U). Since Y was arbitrary, the corresponding ρ-1(U)s clearly cover ρ-1(V ), so f is therefore regular.
Hence, ρ is confirmed a morphism. Now we have to show it for ρ-1
How is ρ-1 defined? Well, with the appropriate permutation of the Mis, my 2.12 work tells me that it's given by (X0,…,Xn) where
| X0 | = (Y 0)1g∕d | (where, remember I can choose ANY of the roots) | ||||
| X1 | = Y 1g∕(X0d-1) | |||||
| X2 | = Y 2g∕(X0d-1) | |||||
 | ||||||
| Xi | = Y ig∕(X0d-1) | |||||
 | ||||||
| Xn | = Y ng∕(X0d-1) | |||||
(again, thank fucking goodness I maintain this blog. With my organization skills, this would have been hidden in one of my three notebooks in opaque context)
By the way, isn't it weird that all those coordinates have analogous definitions except X0. Don't you think, X0 could be put in the same format?
You see, if I write everything in terms of Y 0 (which I'll need to do soon, anyway), I can write:
| X0 | = (Y 0)1∕d | ||
| X1 | = Y 1∕(Y 0(d-1)∕d) | ||
| X2 | = Y 2∕(Y 0(d-1)∕d) | ||
 | |||
| Xi | = Y i∕(Y 0(d-1)∕d) | ||
 | |||
| Xn | = Y n∕(Y 0(d-1)∕d) | ||
Of course, this suggests another definition for X0. Let's confirm (...sorry, those fractions are supposed to be in the exponent. It came out weird):
Y 0∕(Y 0
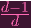 ) ) | = Y
0 ⋅ (Y 0-
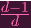 ) ) | ||
= Y 01-
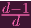 | |||
= Y 0
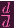 - -
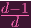 | |||
= Y 0
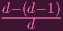 | |||
= Y 0
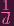 | |||
Hence we can write X0 = Y 0∕(Y 0(d-1)∕d). So, in general, the map ρ-1 is given by
| Xi | = Y i∕(Y 0(d-1)∕d) |
(i = 0,…,n)
Oh.... Since they're all multiplied by the same constant, and we're in projective space, I can actually just write
| Xi | = Y i |
So... ρ-1 is actually just "keep the coordinates 0 through n and drop the rest" I.e., it's given by
| Yi |
 Y i
Y i | (i = 0,…,n) |
... That's a huge improvement over my initial definition...
Okay, with this nice definition of ρ-1, let's confirm the regularity property. Given V open in Pn, and f : V → k regular, we want to verify that f ∘ ρ-1 : ρ(V ) → k is regular.
Suppose f = g∕h on an open U of V , h nowhere zero on U. Consider some Y ∈ ρ(U). Then...
| f ∘ ρ-1(Y ) | =
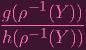 | ||
=
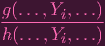 | |||
(now you perhaps see why I did all that work to rewrite ρ-1). Again, h(…,Y i,…) = 0
 h(ρ-1(X)) = 0
yielding a contradiction, so h is nowhere zero on ρ(U). And although g,h came from k[x0,…,xn], we can
interpret them as elements of k[y0,…,yN], so g∕h gives f ∘ ρ-1 as a rational function on ρ-1(U). Since U was
arbitrary, f ∘ ρ-1 is regular on ρ-1(V ) DUN.
h(ρ-1(X)) = 0
yielding a contradiction, so h is nowhere zero on ρ(U). And although g,h came from k[x0,…,xn], we can
interpret them as elements of k[y0,…,yN], so g∕h gives f ∘ ρ-1 as a rational function on ρ-1(U). Since U was
arbitrary, f ∘ ρ-1 is regular on ρ-1(V ) DUN. It's been a while since I've uploaded in consecutive days.... Perhaps I can keep it up? What's that? Those strange letters are still written on my lips? Well, reader, you know what to do ... muahahahahaha, with a strong "muah".