I.2.9b
2/13/2021

Hey, who remembers the twisted cubic curve?
Guess what? I(Y ) = (y - x2,z - x3) = (y - x2,z - xy)! I've already done that part back in
1.2. YAAAAAYYYY. Now I have to figure out I(Y ), and here is where I got stuck for 3 fucking
days.
Read at your own risk. What follows is amateur math hell.
Okay: midway, in the midst of trying way too overcomplicated stuff and going insane (I was originally trying to compute it
using the I(Y ) = Sβ(I(Y )), which you'll have to forgive me for since part fucking a was all about that equation),
I had to look up the Wikipedia page on it to unstuck myself. And according to the wikipedia page, generators
are:
| F0 | = XZ - Y 2 | ||
| F1 | = Y W - Z2 | ||
| F2 | = XW - Y Z |
And there we are. That's the answer. YAAAAAAAAAAAAAY ONTO THE NEXT POST just kidding obviously I have to show why these are the generators blah blah fuck.
Following the exposition of this exercise, I can start by finding a set isomorphic to Y in projective space. I.e. Let me construct some T ⊂ Sh such that
 | (1) |
is a homeomorphism.
(BTW: to match the Wikipedia article, I'm going to let the coordinate ring of P3 be S = k[X,Y,Z,W], and, to
match my old work, I'll let the coordinate ring of A3 be k[x,y,z]).
So given (a,b,c,d) ∈ Z(T) ∩ U0, I need
| ϕ0(a,b,c,d) | ∈ Y | |||||
 ϕ0(a,b,c,d) ϕ0(a,b,c,d) | = (t,t2,t3) | (Definition of affine twisted cubic) | ||||
 (b∕a,c∕a,d∕a) (b∕a,c∕a,d∕a) | = (t,t2,t3) | (Definition of ϕ0) | ||||
Hence we must have
| (b∕a)2 | = c∕a | ||
| (b∕a)(c∕a) | = d∕a |
(like back in 1.2, the second equation could be replaced by (b∕a)3 = (d∕a))
Some basic algebra yields:
| b2 | = ac | ||
| bc | = ad |
i.e. (a,b,c,d) must satisfy the homogenous polynomials:
| F0 | = XZ - Y 2 | ||||
| F2 | = XW - Y Z |
And thus, if you set T = F0,F2, then ϕ0 does become a homeomorphism (boringly verified in my mystical notes), as needed.
"Hmmm, aren't we missing something? Where's F1 from the Wikipedia page?" Good question, reader! Now we do have,
| Y | = Z(T) ∩ U0 | ||
 Y Y | = Z(T) ∩ U0 |
But careful not to repeat my own errors, I know that it's NOT necessarily the case that Y = Z(T) ∩ U0. All I know is that Y ⊂ Z(T) (since Y is supposed to be the smallest closed subset containing Z(T) ∩ U), and supposedly I get to Y from Z(T) by adding F1 to it.
In fact, I know for sure that Y ≠Z(T) ∩ U0. Why? The exercise tells me so. F0 and F2 are precisely the elements β(y - x2),β(z - xy), and the exercise tells me that those don't generate the ideal (EXTREMELY UNINTUITIVE: β(generators of I(Y ))≠ the ideal generated by β(I(Y ))).
So where does the third generator, F1 = Y W -Z2 come from? Answer: I. HAVE. NO. FUCKING. IDEA. Look: once you add F1, the matter of showing that you do get I(Y ) is certainly doable, as I'll show. But I have no idea how you're supposed to come up with F1 = Y W -Z2 from scratch. I mean, look, in the (a,b,c,d) example (in U0), you can think of this as
| bd - c2 | = 0 | (2) |
| ⇐⇒bd | = c2 | (3) |
| ⇐⇒(b∕a)(d∕a) | = (c∕a)2 | (4) |
Which represents the relationship xz = y2 in affine space. This relationship applies for the affine twisted cubic since clearly tt3 = (t2)2, but this relationship is extraneous for the affine twisted cubic. Why isn't it extraneous for the projective twisted cubic. Well, I'm actually about to show that (since the exercise wants me to), but how was I supposed to find this nonextraneous relationship without knowing it beforehand. Everything I could find online just assumes you've already incorporated this extra generator.
Now, I tried to get it "from scratch". Let me take you part of the way there. Let Y = Z(T′). Recall, I know that Z(T′) ⊂ Z(T). So if there's any element P in Z(T′) = Y = Z(T′) ∩ U0 that are not in Z(T′) ∩ U0, then it would have to be outside of U0. I.e. denoting P = (a,b,c,d), this P would have a = 0. But again, since P ∈ Z(T), we'd at least need the previous equalities to hold:
| b2 | = ac | ||
| bc | = ad |
Now combining this with a = 0, it's clear that we must also have b = 0. Which means P = (0, 0,c,d).
That is as far as I can get. I tried using the definition of closure (that every neighborhood containing P has a nonempty intersection with Z(T′) ∩ U0), but this is too much abstraction for me to do anything.
Fine, let's add this fucking F1 in. Let's let R = T ∪ {F1}. In which case, for this point P we've been discussing, factoring the additional restriction (2), we'd need to have c = 0. So then we'd actually have P = (0, 0, 0,d) = (0, 0, 0, 1) (this is presumably the "point at infinity" that the Wikipedia page refers to). I.e. there is only one point that Z(R) contains that Y = Z(T) ∩ U0 does not. Now that I added F1 to make R, I can actually show that Z(R) = Y . Well, again, since Y is the smallest closed set containing Y , Y ⊂ Z(R) (Z(R) contains Y because as analyzed earlier, adding it is harmless in affine space, i.e. adding it is harmless on U0: Z(R) ∩ U0 = Y ). Now, if that inclusion were proper, then we'd have to have Y = Z(R) ∩ U0. So we'd have Y = Z(R′) for some R′. And looking online told me that the key point is to note that there would have to be some f ∈ R′ where f vanishes on all of Y but not on (0, 0, 0, 1). Here's a proof of why that can't happen. I'm not transcribing it here. WHAT? I'VE ALREADY SPENT SO MUCH TIME ON THIS EXERCISE GIVE ME A BREAK FFFFFFFFFFFUUUUUUUUUUUUUUUUUU.
So Y = Z(R) = Z(F0,F1,F2) indeed. Taking I of sides...
| I(Y ) | = I(Z(F0,F1,F2)) | ||
=
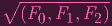 | |||
| = (F0,F1,F2) |
The last equality follows from LOL I'M TOO LAZY TO VERIFY IT. I expect that the work to show that (F0,F1,F2) is prime is similar to what I did back in 1.2: take the quotient and show that it's an integral domain. I'm not doing that, folks. Not today. My brain is so fucked right now.
*Gasp* *Gasp*. Okay. Last thing the exercise asks us to show is essentially that (F0,F2) ⊊ (F0,F1,F2) (We showed that Y = Z(R) ⊂ Z(T), and now we're going to show that this inclusion is in fact proper). And this comes from my earlier analysis of "P" With just the first two restrictions, we can have any point of the form P = (0, 0,c,d). But adding F2 means that we have to exclude everything but P = (0, 0, 0, 1).
AND WE ARE FUCKING DONE.
THREE DAYS OF GETTING PWNED.
AND I STILL DIDN'T REALLY COME OUT ON TOP
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA.
Dude. I'm fucking melting. I'm fucking so exhausted. I still don't know how you're supposed to just fucking get the F1 thingy out of nowhere. Agh this post probably has so many typos. Fuck. I'll proofread it later. Right now I just need to post this madness. The reason I made this blog was so that I don't have to bottle all this up. My eyes hurt. Ow.