*AHEM*

Hole in my heart? More like hole in my proof. Yes, reader, just remember.. You remember, right? C is irreducible.... C is irreducible.... You're being hypnotized.... Yess..... Now....... lick my dick..........

Talk about an asspull. Yes, I pulled that one out of the hole in my ass, persay. For whatever reason, since Z(β(T′)) ∩ U was irreducible, I assumed that Z(β(T′)) was irreducible. NOT necessarily true. Z(β(T′)) is merely a closed set. There's not much reason to assume it's irreducible right off the bat.

Well, what do then? It's thanks to that asspull that I was able to say

(1)

and perform a series of steps that got me to

(2)

HOLD ON. The first equation is an equality, but second equation is an inclusion. There might be some wiggle room here. Check it out:

Y	= clPn(Z(β(T′)) ∩ U)
	⊂ clPn(Z(β(T′)))
	= Z(β(T′))	(closure of closed set)

Okay, okay, steady... steady... Now, let me follow yesterday's work except paying attention to the inclusion.:

I(Y )	⊃ I(Z(β(T′)))	(I reverses inclusion)
	=	(Nullstellensatz)
	⊃ Sβ(T′)

And there's (2) again.

Phew, my proof just barely hangs together. We are SAFE!
One more thing:
I asked you to take for granted that

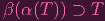(3)

claiming that "it's in my notes" (lol), then proceeded to conclude.

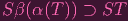(4)

Let me justify that:
Grab some element f from T ⊂ S^h, like let's say (working in P³)...

f(w,x,y,z)	= wxy + w2x + w3 + xyz
α(f)	= xy + x + 1 + xyz	definition of α
β(α(f))	= w3( + + 1 + )	definition of β
	= wxy + w2x + w3 + xyz
	= f

Hmph, interesting... β(α(f)) = f. Let's try an example where all terms have a w:

f	= wxy + w2x + w3 + wyz
α(f)	= xy + x + 1 + yz
β(α(f))	= xy + wx + w2 + xz
	= f∕w

The pattern you'll see is that β(α(f)) = f∕(w^r) for some int r ≥ 0. "Wait, doesn't this lay doubt on equation (3)??" Indeed it does, because it's PROBABLY WRONG. *Applause*. Ahh, thank you, thank you *Bow*. I'd like to thank my family, my friends, and all my loyal fans...

Okay, so we don't exactly recover f the way we want, but if β(α(T)) were an ideal, then we could say that

wrβ(α(f))	= wr
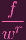	= f

thereby recovering f. Which is why, DUN DUN DUN, (4) is actually CORRECT. So we are, you know...