WTF is this? Why am I taking an affine set, moving it to Pⁿ, and taking its closure? IDK. To quote a wise soul:

And with that, let's get started.

We have worked with the homeomorphism ϕ₀ before, and in particular here are the details of the β they refer to:


(Btw: You know how where it says "straightforward checking" and "one checks easily...". I never actually checked these. Muahahahahaha).
I'll be using this proof quite a bit. Like the proof, I may sometimes use U and ϕ sinstead of U₀ and ϕ (though note the Y in this exercise is sorta different from the Y in theirs. CAREFUL).

NOTE: In this exercise, we care not about the set β(I(Y )) ⊂ S^h itself but the ideal generated by β(I(Y )) in S, which is denoted Sβ(I(Y )) ⊂ S. So our goal is to show that I(Y ) = Sβ(I(Y ))
Also, like earlier, the "bar" notation for closure is kinda confusing. Here's the definition of this exercise's Y in the trusty cl notation:

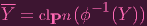(1)

Alright, ready for some messy business? Okay. Since Y is an affine variety, I can write Y = Z(T′) for some T′⊂ A. And the 2.2 proof tells us that ϕ^-1(Y ) = Z(β(T′)) ∩ U₀. Taking the closure cl_Pⁿ of both sides, we get

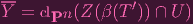(2)

Well, that's an ugly right hand side. Let's actually try to figure out that that closure is. I would LIKE to get rid of the U. Can I? I got stuck here for a while, and then I decided to invoke this good old property just to see what happens:

"If A is a subspace of X containing S, then the closure of S computed in A is equal to the intersection of A and the closure of S computed in X: cl_AS = A ∩ cl_XS"

Let me write C = Z(β(T′)) for simplicity.
Remember that C is irreducible, so by 1.6,

(3)

Now, using that property,

clC(C ∩ U)	= clPn(C ∩ U) ∩ C
clC(C ∩ U) ∩ C	= C	using (3)
clPn(C ∩ U)	⊃ C

But clPⁿ(C ∩ U) would have to be the smallest closed set containing C ∩ U, meaning that clPⁿ(C ∩ U) ⊂ C.
Hence clPⁿ(C ∩ Y ) = C. I.e. (2) turns into

(4)

(Man that closure property has saved my butt more than once).

Now, we care not about this mysterious β(T′), but β(I(Y )). That's okay, because remember that T′ and Y are related by Y = Z(T′). And we can assume without loss of generality that our T′ is not just a subset of A, but a prime ideal in A, hence, I(Y ) = T′. We're trying to figure out what I(Y ) is, so let's take I of both sides:

(5)

As you can see, we're getting closer to what we need (NOTE: I'll write T′ = I(Y ) for simplicity, so my goal is to show I(Y ) = Sβ(T′)). Remember, we care about the ideal Sβ(T′), not the set β(T′). Fortunately, By definition of Z in Pⁿ, we have Z(Sβ(T′)) = Z(β(T′)) (I'm PRETTY sure. *Note to self: may wanna double check this lol) so we can rewrite (4) as:

(6)

Great! Now just apply the Nullstellensatz and we get

I(Y )

=

NNNNNNNNNNOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO. THE SQUARE ROOT. ARRRRRRRRGGGGGGHHH. ALL THIS TELLS US IS THAT I(Y ) ⊃ Sβ(T′). I need to show either that Sβ(T′) is radical, or the reverse inclusion. UGGGGHHHH.

(also I like how I'm calling it a "square root" even though it's not meant to be that lol... "radical" is the right word).

So I tried showing Sβ(T′) to be radical (or to be prime) and... it didn't quite work out for me. I don't know if there's a good way to do that directly, but I settled on showing the reverse inclusion instead. I.e. I want to show that Sβ(T′) ⊃ I(Y ):

Look above at the proof of 2.2 again. To show the inclusion we have so far I used the part about W ("Conversely, let W be..."). SO, perhaps for the reverse inclusion, I can use the part about α and Y , where their "Y " is analogous to our ϕ^-1(Y ). What does it tell us? Well, firstly, clPⁿϕ^-1(Y ) = Z(T) for some T ⊂ S^h (i.e. Y = Z(T)). And if you let T′′ = α(T). Then it turns out that ϕ(ϕ^-1(Y )) = Z(T′′). I.e. Y = Z(T′′). Also, remember that Y = Z(T′), so Z(T′) = Z(T′′)... but T′ and T′′ are not necessarily equal (one is prime ideal and the other is just a set). Actually, T′′⊂ T′ ( T ′′ ⊂ I(Z(T′′)) = I(Y ) = T′ ).

Motherfuck.

MOTHERFUCK.

I told you this was going to be messy.

Now, reader, I'm going to have you take for granted that

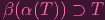(7)

I'll justify it later (EDIT: didn't get around to typing this up lol. It's in my notes). Since T′′ = α(T), we're actually saying that β(T′′) ⊃ T. Now taking the ideal generated by both sides, we get

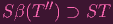(8)

Why does this help us? Well, remember Y = Z(T). So taking I of both sides here. yields I(Y ) = . NNNNOOOOOOOOOOOOOOOOOO, IT'S ANOTHER SQUARE ROOT (I mean "radical") IN OUR WAY. WAIT. We can get around this. is a homogenous ideal, i.e. generated by homogenous elements. So we can assume without loss of generality that T ⊂ S^h is precisely such a set of generators (since there were no requirements on T) AND HENCE = ST. I.e. I(Y ) = ST. Now using equation (8), we have Sβ(T′′) ⊃ I(Y ). OOPS. We have an extra apostrophe. I was trying to show S(β(T′)) ⊃ I(Y ). How do I get rid of that apostrophe! NNNNNNNOOOOOOOOOOOOOO IT'S AN APOSTROPHE IN OUR WAY. Actually, no worries, I already showed that T′′⊂ T′. So β(T′′) ⊂ β(T′) and Sβ(T′′) ⊂ Sβ(T′). Hence

Sβ(T′)	⊃ Sβ(T′′)
	⊃ I(Y )

AND. WE. ARE. FUCKING. DONE.
Holy FUCK. Was that supposed to be THAT FUCKING COMPLICATED? I'm guessing I did this in an extremely inefficient way.
That was bad, but I'm even more worried about part (b).