Welll... Might as well quickly crank out another one before I go to bed. It's yet another projectivization of affine question. Here's the affine version:

And unlike some of the trickier exercises like the last two, we can just follow the affine proof for this one. Here's Theorem 1.11A, which we'll use:

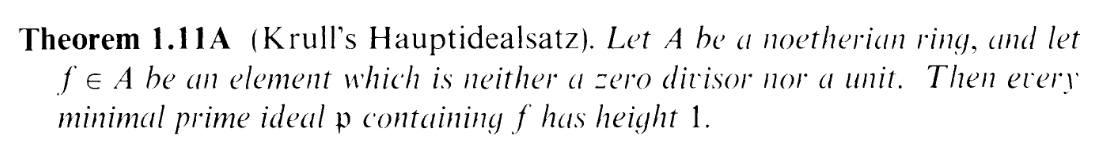
And also Theorem 1.8A:

Since Y is a variety, note that I(Y ) is prime. And here's my slick proof:

dim Y	= n - 1
⇐⇒ dim Y + 1	= n	(Adding 1 to both sides)
⇐⇒ dim S(Y )	= n	(by 2.6)
⇐⇒ dim k[x0,…,xn] - htI(Y )	= n	(by 1.8A)
⇐⇒n + 1 - htI(Y )	= n
⇐⇒htI(Y )	= 1
⇐⇒I(Y )	= (f)	where f satisfies the requirements

That last equality is thanks to 1.11A and observing that in UFDs, f is prime iff it is irreducible. (Yes I put this sentence outside of the align environment to prevent it from going outside my post because I still haven't figure out how to fix that FffFFFFFFFFFFFFFFFffFUUUUUGG)