I.2.14
3/2/2021

Hi. This post will be quick and dry (just like sex with your wife, hahaha). Yes, an extremely scary-looking exercise. But it's actually a very similar process to what I did in 2.12b . In fact, it's even
easier.
Letting θ denote the k[{zij}] → k[x0,…,xr,y0,…,ys] map the hint gave us, we set α = ker θ and we wanna
show that imϕ = Z(α).
"One inclusion is easier than the other," said 2.12b, and the statement holds analogously here. Give me a point
P = (a0,…,ar) × (b0,…,bs) ∈ Pr × Ps, so that ϕ(P) = (…,aibj,…). Now give me an f(…,zij,…) ∈ α.
| f(…,zij,…) | ∈ ker θ | ||
 θ(f(…,zij,…)) θ(f(…,zij,…)) | = 0 | ||
 f(…,θ(zij),…) f(…,θ(zij),…) | = 0 | ||
 f(…,xiyj,…) f(…,xiyj,…) | = 0 | ||
 f(…,ai,bj,…) f(…,ai,bj,…) | = 0 | ||
 f(ϕ(P)) f(ϕ(P)) | = 0 | ||
Since f ∈ α was arbitrary, ϕ(P) ∈ Z(α). And since P was arbitrary, imϕ ⊂ Z(α)
Now for the reverse inclusion. Given C = (…,cij,…) ∈ Z(α), can we find P = (a0,…,ar) × (b0,…,bs) ∈ Pr ×Ps such that ϕ(P) = C
I.e. we need to satisfy (…,aibj,…) = (…,cij,…).
I.e. we need to satisfy aibj = cij (up to a constant multiple independent of i,j).
So what do we do? Same thing in 2.12b: Line up the requirements, "force" values for our ai,bjs, verify that they actually work.
First, I'll assume that c00≠0 without loss of generality. Now, let a0 be.... anything but zero. Yes. You heard me right. Let a0 be literally fucking anything you want it to be, reader, as long as it's nonzero and from k.
Then check out these requirements:
| a0b0 | = c00 | a0b0 | = c00 | ||||
| a0b1 | = c01 | a1b0 | = c10 | ||||
 |
 | ||||||
| a0bj | = c0j | aib0 | = ci0 | ||||
 |
 | ||||||
| a0bs | = c0s | arb0 | = cr0 | ||||
As soon as a0 is fixed, so is everything else:
| b0 | = c00∕a0 | a0 | = c00∕b0 | ||||
| b1 | = c01∕a0 | a1 | = c10∕b0 | ||||
 |
 | ||||||
| bj | = c0j∕a0 | ai | = ci0∕b0 | ||||
 |
 | ||||||
| bs | = c0s∕a0 | ar | = cr0∕b0 | ||||
So choosing anything for a0 forces all of P. Now we just have to check that ϕ(P) does indeed equal C. I.e. we need to check if aibj = cij. Well, based on our settings,
| aibj | =
 | ||
=
 | |||
Now suppose, for the sake of contradiction,
 did NOT equal cij. Then that would mean
did NOT equal cij. Then that would mean
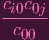 | ≠cij | ||
 ci0c0j ci0c0j | ≠cijc00 | ||
 ci0c0j - cijc00 ci0c0j - cijc00 | ≠ 0 | ||
I.e. we'd have that C does NOT satisfy the polynomial
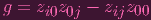 |
But, of course,
| θ(g) | = xiy0x0yj - xiyjx0y0 | ||
| = 0 |
So g ∈ ker θ i.e. g ∈ α. By assumption, C ∈ Z(α), yielding a contradiction.
Don't worry. The next exercise is another 3-parter.