II.1.20b
1/9/2022
B
(Γ notation, for anyone confused) So to be clear, the reason I'm skipping part A is
because it's boring. Again, yours truly has to practice divvying up their time
wisely, so I'm gonna spend it on stuff where we actually get stuff done, like this:
 | (1) |
We wanna show that it's exact, and uhhh... the thing about "flasqueness".. whose
definition is given in 1.16... which I didn't do:

I didn't do it yet because it's 5 parts and that scares me. HOWEVER for now the
point that the restriction maps would be surjective is all we need, so we can
continue.
Alrighty, so what we've learned in Hartshorned II so far is that it's easier to show
exactness on the stalk level. Let's go ahead and define ϕ and ψ and get their
stalky equivalents
0.1 Defining ϕ
To create
ϕ :
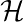 Z0( Z0(
 ) ) | →
 |
We need to define, given V ⊂ X,
ϕ(V ) :
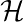 Z0( Z0(
 )(V ) )(V ) | →
 (V ) (V ) |
And evidently the LHS is the complicated one, so let's unwrap that baby:
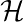 Z0( Z0(
 )(V ) )(V ) | = Γ
Z∩V (V,
 |V ) |V ) | |||||
= {s ∈ Γ(V,
 |V )|Supps ⊂ Z ∩ V } |V )|Supps ⊂ Z ∩ V } | ||||||
= {s ∈ Γ(V,
 |V )|Supps ⊂ Z} |V )|Supps ⊂ Z} | (since Supps ⊂ V trivially) | |||||
= {s ∈ i-1
 (V )|Supps ⊂ Z} (V )|Supps ⊂ Z} | (where i : V
 X the inclusion) X the inclusion) | |||||
= {s ∈ lim i(W)⊃V
 (W)|Supps ⊂ Z} (W)|Supps ⊂ Z} | ||||||
= {s ∈ lim W⊃V
 (W)|Supps ⊂ Z} (W)|Supps ⊂ Z} | ||||||
= {s ∈
 (V )|Supps ⊂ Z} (V )|Supps ⊂ Z} | ||||||
Okay, that's a bretty good description of the sections over V , and furthermore,
it's now clear that
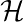 Z0( Z0(
 )(V ) ⊂ )(V ) ⊂
 (V ) (V ) |
so ϕ(V ) can just be the inclusion! And ϕP is also the inclusion! EZ.
0.2 Defining ψ
Okay, now we need
ψ :
 | → j*(
 |U) |U) |
So we define for V ⊂ X open,
ψ(V ) :
 (V ) (V ) | → j*(
 |U)(V ) |U)(V ) |
Unwrapping the RHS...
j*(
 |U)(V ) |U)(V ) | =
 |U(j-1(V )) |U(j-1(V )) | |||||
=
 |U(U ∩ V ) |U(U ∩ V ) | ||||||
= j-1
 (U ∩ V ) (U ∩ V ) | (Kinda did a double take here cuz we used both the direct image and restriction on the same sheaf using the same map lol. trippy af) | |||||
= lim W⊃j(U∩V )
 (W) (W) | ||||||
= lim W⊃U∩V
 (W) (W) | ||||||
=
 (U ∩ V ) (U ∩ V ) | ||||||
Which makes the most natural definition for ψ(V ) to be the restriction map
WHICH, btw, if
 is flasque, we know is surjective. BUT obviously remember
that don't matter cuz we gotta check surjectivity at the stalk level, which i'm
about to do, lol
is flasque, we know is surjective. BUT obviously remember
that don't matter cuz we gotta check surjectivity at the stalk level, which i'm
about to do, lol
So uh, I'd just like to say that the stalks of j*(
 |U) are pretty weird. Basically
the equivalence relation giving rise to (j*(
|U) are pretty weird. Basically
the equivalence relation giving rise to (j*(
 |U))P works like this: To determine
if [V,s] = [W,t] (V,W neighborhoods of P), we consider if there's any open set
contained in V ∩U and W ∩U where s and t restrict to the same section. The
weird part is that V ∩ U and/or W ∩ U might NOT contain P itself, but
that's just how the equivalence relation works. "Dude, this is confusing." I
KNOW, IT TRIPPED ME UP FOR A WHILE LOL. Just... think about it.
|U))P works like this: To determine
if [V,s] = [W,t] (V,W neighborhoods of P), we consider if there's any open set
contained in V ∩U and W ∩U where s and t restrict to the same section. The
weird part is that V ∩ U and/or W ∩ U might NOT contain P itself, but
that's just how the equivalence relation works. "Dude, this is confusing." I
KNOW, IT TRIPPED ME UP FOR A WHILE LOL. Just... think about it.
Okay, actually, you know what? I'm a adult. I know I don't act like one on this
page, nor do I irl (And honestly, it's extremely embarassing and I'm ashamed of
who I am. It's legitimately shocking that I'm continuing to live with myself like
this. I'm embarassed to even talk to people and show myself in public because the
way I carry myself visibly reveals how mentally underdeveloped I am.
People can tell that something is wrong with me just by looking at me. I
can feel the weight of all the eyes on me: I feel it on my unkempt hair,
submissive smile. I look unnatural. Dissocietal. My mind comes through in
my fingers and the way I flinch and tremble at the sight and touch of
other people outs me as inhuman. Why am I like this? I love people,
I really do, but I don't know how to connect with them. I don't know
how to behave around them. I want to be closer to them, and yet all my
life I've been so estranged from them. I just want to be able to have a
normal conversation with someone. I see people talk, and I start beaming in
admiration as they make some hilarious comment and roar in laughter. I
want to be like that. I want to be able to make a hilarious comment, or
roar in laughter. I want to be a part of the excitement, a part of the
moment. But I can't enter into that circle. It doesn't happen. It just
doesn't work. My grand entrance makes everything awkward. My comments
fall flat. My presence is at best unfelt and at worst a nuisance. Always.
No matter how nice and accomodating they are to me, I can't fit in. I
don't know how to talk. I've gotten better at it over the years, but not
enough. Not enough to actually be an influence on someone. In a groups,
everyone takes turns dominating the conversation except me, in some kind of
unsaid round robin that I didn't sign up for. One-on-one, people talk
about things they've done and experienced that genuinely impress me,
and yet all I can respond is "That's cool," and thus sound colder than I
actually feel. I sound unimpressed and bored when I'm not. I try to ask
followup questions, but I don't know anything about anything. I'm so
ignorant of everything–things that normal people would know how to talk
about like housing prices uptown and the latest tech–and the babyish
questions and comments I offer invariably douses their flame. I'm not
able to engage on their level. I can't engage on anyone's level, because
my knowledge of everything is so stunted. Then, apparently giving up,
they ask me what I've been up to. And here I always turn up a blank.
Why am I never prepared for this question? I've been asked it so many
times, and yet I always let it kill the conversation. Nothing. I've been up
to nothing. Please don't ask me that. I don't want to talk about me. I
have nothing. I'm sorry for being a rock. I'm sorry for making everything
awkward. I'm sorry, I'm sorry. Why am I like this? I hate it. I want to cry. I
want it to end. Please, let me in. Let me in... Please... What? No I'm not
going to wear a mask lol suck my co–) but I've been Hartshorned long
enough to EXPRESS THIS IN FANCY MATHEMATICAL NOTATION:
(j*(
 |U))P |U))P | = lim V ∋P
 (V ∩ U) (V ∩ U) |
There you go. *Phew*. Now I'd like you to note that in the case that, in the
direct limit, if V ∩U is always empty I.E. IF P IS NOT IN THE CLOSURE OF
U, then the stalk is 0. Otherwise, ψP is just < V,s >
 [V,s]. Either way, it's
surjective if
[V,s]. Either way, it's
surjective if
 is flasque. IN FACT, if it's flasque, we can add an extra → 0 to
(1) and make it a short exact sequence. Well, flasque or not, to finish this exercise
off we need to show
is flasque. IN FACT, if it's flasque, we can add an extra → 0 to
(1) and make it a short exact sequence. Well, flasque or not, to finish this exercise
off we need to show
0.3 exactness at the middle
that imϕP = ker ψP. So let's split it up into cases:
0.3.1 P
 U
U
In this case, as we explained, (j*(
 |U))P = 0, so ker ψP =
|U))P = 0, so ker ψP =
 P, and in
particular, ∃ a neighborhood V of P such that V ∩ U = ∅. Now let's suppose
that < W,s >∈
P, and in
particular, ∃ a neighborhood V of P such that V ∩ U = ∅. Now let's suppose
that < W,s >∈
 P. Refining, if necessary, assume that W ⊂ V . Then
P. Refining, if necessary, assume that W ⊂ V . Then
| W ∩ U | = ∅ | ||
 W W | ⊂ Z | ||
 Supps Supps | ⊂ Z |
So s ∈
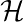 Z0(
Z0(
 )(W), and therefore < W,s >∈ imϕP. So
)(W), and therefore < W,s >∈ imϕP. So
 P ⊂ ϕP and the
reverse inclusion is trivial.
P ⊂ ϕP and the
reverse inclusion is trivial.
0.3.2 P ∈U
Ok this is the normaller case. Suppose < V,s >∈ imϕP. We can assume
without loss of generality that its preimage was also < V,s > (derefining–erm,
coarsifying if necessary) and therefore that Supps ⊂ Z. Using that WLG, let's
write
| < V,s > | ∈ imϕP | |||||
| ⇔Supps | ⊂ Z | |||||
| ⇔∀Q ∈ V : sQ≠0 |
 Q ∈ Z Q ∈ Z | |||||
| ⇔∀Q ∈ V : sQ≠0 |
 Q Q
 X - Z X - Z | |||||
| ⇔∀Q ∈ V : sQ≠0 |
 Q Q
 U U | |||||
| ⇔∀Q ∈ V : sQ≠0 |
 Q Q
 U U | |||||
| ⇔∀Q ∈ V : Q ∈ U |
 sQ = 0 sQ = 0 | (CONTRAPOSITIVE BITCHESSSSSSS) | ||||
| ⇔ρV,V ∩U(s) | = 0 | |||||
| ⇔ψ(V )(s) = 0 | ||||||
 ψP(< V,s >) ψP(< V,s >) | = 0 | (C-C-C-C-C-C-C-C-COMBO BREAKER) | ||||
| ⇔ < V,s > | ∈ ker ψP |
ARRRRRRRRGGGGHHHH THAT ONE
 RUINED THE
CHAIN OF ⇔s. WE ONLY GOT ONE SIDE OF THE INCLUSION.
NOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO. Okay, don't panic:
It's just refining lol; the same way we squeezed out the first ⇔. MR.
RUINED THE
CHAIN OF ⇔s. WE ONLY GOT ONE SIDE OF THE INCLUSION.
NOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOO. Okay, don't panic:
It's just refining lol; the same way we squeezed out the first ⇔. MR.
 , I
SHALL NOW GRANT YOU YOUR LEFT WING. YOU ARE NOW A ⇔. *Clap
clap clap*. And that finishes the exercise.
, I
SHALL NOW GRANT YOU YOUR LEFT WING. YOU ARE NOW A ⇔. *Clap
clap clap*. And that finishes the exercise.
The next one is a 5 parter so it might take a while for the next post, unless I split
it up... Yea, sorry for turning these out so slowly lol. I'm trying to speed it up,
but... AGGGHH. 2 more exercises left for this section!!! Almost there!
