II.1.21cde
1/14/2022

AWWW, YES. We're finally relating what we've learned here a bit back
to chapter 1. EXCITING! Get ready for some EBIC NOSTALGIABAIT! But first,
A
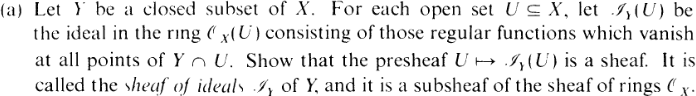
>Verify that this presheaf is a sheaf
BOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOOORING. Skipping this
one. It's NOT that I can't do it. It's just NOT WORTH IT. Bleh.
B

Got stuck lol [Might add more detail later].
C

Okay, FINALLY here's one I did. We wanna show the exactness of
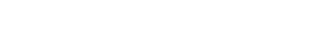 | (1) |
which, as usual, we'll do at the stalk level. But first let's make these maps...
Errr... Actually by definition

 is a subsheaf of
is a subsheaf of
 X, so ϕ can just be the
inclusion. For ψ on the other hand, we need to, given an open set U, define
X, so ϕ can just be the
inclusion. For ψ on the other hand, we need to, given an open set U, define
ψ(U) :
 X(U) X(U) | →
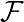 (U) (U) |
Okay. Let's go ahead and unwrap the RHS:
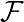 (U) (U) | = i*
 P(U) ⊕ i* P(U) ⊕ i*
 Q(U) Q(U) | ||
| = |
Okay lol, so before we move on, what does i*
 P look like? I mean, first of all, the
regular functions on a singleton are necessarily just gonna be constant functions.
So if P ∈ U, then it just becomes k. Otherwise U ∩{P} = ∅, yielding a 0...
Wait a second....
P look like? I mean, first of all, the
regular functions on a singleton are necessarily just gonna be constant functions.
So if P ∈ U, then it just becomes k. Otherwise U ∩{P} = ∅, yielding a 0...
Wait a second....

HIGHER ON THE SHEAVES. AND I KNOW IT'S MY TIME TO GO.
uhh yea, so basically my point here is that i*
 X is a skyscraper sheaf on the
point P with the constant ring k. AIN'T THAT SOMETHING? So depending on
whether P and Q are in U,
X is a skyscraper sheaf on the
point P with the constant ring k. AIN'T THAT SOMETHING? So depending on
whether P and Q are in U, i*
 P(U) ⊕ i* P(U) ⊕ i*
 Q(U) Q(U) | = (k or 0) × (k or 0) |
(× is the same as ⊕ for finite products of groups) AND THUS, the natural map
for ψ(U) is just plain ol' evaluation
| f |
 f(P) × f(Q) f(P) × f(Q) | (taking f(L) = 0 if f not defined at L) | ||||
Okay, now let's drop down to the stalk level and get exactness there:
 | (2) |
Now, erm... I'm just gonna assume the direct product commutes over stalks...
EXERCISE LEFT 2 READER:
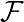 R R | = (i*
 P(U) ⊕ i* P(U) ⊕ i*
 Q(U))R Q(U))R | ||
= (i*
 P(U))R ⊕ (i* P(U))R ⊕ (i*
 Q(U))R Q(U))R |
AWW YEA, MULTISTALK DRIFTING. And thanks to our work in 1.17, I
know that these stalks are just k or 0, depend on R's inclusion in the closures of
P and Q.... HOWEVER.... Recall this is X = P1, in which singletons are
already closed!! So really, this depends on whether R is P or Q. And since P
and Q are distinct...
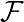 R R | =
 |
Either way, ψP is clearly surjective (trivial for
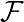 R = 0 and the constant
functions cover
R = 0 and the constant
functions cover
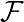 R = k). So now all we have to verify for exactness of (2) is...
R = k). So now all we have to verify for exactness of (2) is...
imϕR
 ker ψR ker ψR |
Which I'll split into cases.
0.1 CASE: R
 {P,Q}
{P,Q}
Then
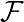 R = 0 and ker ψR = (
R = 0 and ker ψR = (
 X)R. Oh, probably a good time to
mention now that by virtue of ϕP being an injection, we can identify
imϕP = (
X)R. Oh, probably a good time to
mention now that by virtue of ϕP being an injection, we can identify
imϕP = (
 Y )R. OKAY. Now since S = {P,Q} is closed, we can obtain
a neighborhood V or R that does not intersect S. Then CLEARLY,
Y )R. OKAY. Now since S = {P,Q} is closed, we can obtain
a neighborhood V or R that does not intersect S. Then CLEARLY,
 Y (V ) Y (V ) | =
 X(V ) X(V ) |
(since the restrict to 0 condition is vacuously true), and the same for all smaller
neighborhoods of R, hence yielding
(
 Y )R Y )R | = (
 X)R X)R |
i.e. imϕR = ker ψR. Done
0.2 CASE: R = P or Q
Assume wlg R = P. Then
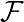 P = k, and
P = k, and
ker ψP = {< V,f >∈
 X|f(P) = 0} X|f(P) = 0} |
Which if ya think about it, is basically just a description of (
 )P. So we're done,
haha.
)P. So we're done,
haha.
0.3 SURJECTIVE BUT NOT SURJECTIVE
So here's an example of the famous OOPSIE that we've kept run into about
surjectivity. We gotta show that the map of global sections
ψ(X) :
 X(X) X(X) | →
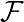 (X) (X) |
is NOT surjective (despite ψ being surjective as a whole). Actually, this is ez.
Since both P and Q are in X, I know that
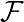 (X) = k ×k. And a theorem I.3.4
all the way back from Chapter I tells us that
(X) = k ×k. And a theorem I.3.4
all the way back from Chapter I tells us that
 X(X) = k. So our map is
X(X) = k. So our map is
| ψ(X) : k | → k × k |
where, following the definition of ψ, the image of ψ is the diagonal, a proper
subset of k × k. DONE.
D
Okay, first thing's first, let's go ahead and make the injection
This becomes obvious when you work out
 . Going by the definition of constant
sheaf, we can write
. Going by the definition of constant
sheaf, we can write
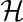 (U) (U) | = {f : U → K|f continuous} | (3) |
Alright, so I fucked this up a couple of times confused as to what was going on...
but then I realized something. Remember, the constant sheaf gives K a discrete
topology, right? I also I know that if f ∈
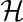 (U), it has to be continuous. Now
let's say s ∈ K is in the image of f (there is at least one such element). Now
take another element t ∈ K. By continuity, f-1(s) and f-1(t) have to both be
open. By assumption, f-1(s) is nonempty, but what about f-1(t). If it's NOT
empty, then it intersects f-1(s), because open sets here are dense. But if s≠t, we
get a contradiction (f has points that map to two different things), so we must
have s = t. So basically, all f does is pick out a point of K... so it can just be
taken as an element of K. So (for nonempty U) I can just rewrte (3) as
(U), it has to be continuous. Now
let's say s ∈ K is in the image of f (there is at least one such element). Now
take another element t ∈ K. By continuity, f-1(s) and f-1(t) have to both be
open. By assumption, f-1(s) is nonempty, but what about f-1(t). If it's NOT
empty, then it intersects f-1(s), because open sets here are dense. But if s≠t, we
get a contradiction (f has points that map to two different things), so we must
have s = t. So basically, all f does is pick out a point of K... so it can just be
taken as an element of K. So (for nonempty U) I can just rewrte (3) as
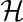 (U) (U) | = K |
LMFAO. What a simplification. Also note, given open U
 |
(was unsure about that last equality at first, but it's thanks to good ol'birational
equivalence)
Wee, so that's our injection.
And now we have to deal with this business about... what's that? Skyscraper
sheaves?

IS A NEW WAY I LIKE TO BE.
I'M. JUST. RUNNING. IN. THE. 90S.
Okay, so we wanna show that
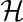 ∕ ∕
 |
 ∑
P∈XiP(K∕ ∑
P∈XiP(K∕
 P) P) | (4) |
Okay, this looks scary, Let's plug in an open U ⊂ X and see what happens.
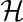 (U)∕ (U)∕
 (U) (U) |
 ∑
P∈XiP(K∕ ∑
P∈XiP(K∕
 P)(U) P)(U) | ||
i.e.K(U)∕
 (U) (U) |
 ∑
P∈UK∕ ∑
P∈UK∕
 P P | ||
OHHHHHHHH BOY. This is some WILD stuff, lol. So sending an element from
LHS → RHS is evidently extremely trivial, but the reverse direction? We have to
match up tons of copies of K to a SINGLE element of K, and our only hope is
taking advantage of our quotient.
WHAT. THE. FUCK. I need to "glue" a bunch of K∕
 P elements into a
SINGLE K(U)∕
P elements into a
SINGLE K(U)∕
 (U) element? This honestly doesn't even seem remotely
possible because there's no restriction on the selections of each K∕
(U) element? This honestly doesn't even seem remotely
possible because there's no restriction on the selections of each K∕
 P
component. Yes, we are actually trying to prove that you can literally just pick a
ton of random elements from K, and somehow when you quotient all of them by
P
component. Yes, we are actually trying to prove that you can literally just pick a
ton of random elements from K, and somehow when you quotient all of them by
 Ps, it glues together into something.
Ps, it glues together into something.
Alright: For the first time in Hartshorned II so far, I am going to look up a
solution. Maybe I should make a counter for how many times I do this (update: it's now on the list page)
UPDATE: I'M RETARDED.
I SOMEHOW forgot to try checking
this at the stalk level. The mantra of sheaves has been "stalks are nice" and I
FORGOT?!!?!:!?!? HOW?????? I know why: Because I was so used to going down
to stalks when it came to the question of exactness; I forgot it would also be
useful for the question of isomorphism. Let's start from (4) and try this again.
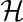 ∕ ∕
 |
 ∑
P∈XiP(K∕ ∑
P∈XiP(K∕
 P) P) | |||||
i.e. (
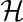 ∕ ∕
 )Q )Q |
 (∑
P∈XiP(K∕ (∑
P∈XiP(K∕
 P))Q P))Q | |||||
i.e.
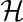 Q∕ Q∕
 Q Q |
 ∑
P∈X(iP(K∕ ∑
P∈X(iP(K∕
 P))Q P))Q | |||||
i.e. K∕
 Q Q |
 (iP(K∕ (iP(K∕
 Q))Q Q))Q | |||||
i.e. K∕
 Q Q |
 K∕ K∕
 Q Q | (from our work on skyscrapers) |
AND THUS THAT QUESTIoN MARK IS NO MORE. DONE. HOW
CONCRETELY THEY ACTUALLY MANAGE TO GLUE TOGETHER IDK,
BUT THE STALKS TELL ME IT'S TRUE, THEREFORE IT'S
TRUE. God bless stalks.
And yes, I know we're on part D and I could make some joke about Initial "D",
but what do we do when the punny butts are before us? Do we bite? When the
dillydallying D-string butt's beckoning you to sacrifice your morals and senses at
its cheeky altar: Remember the wise magazine that once said "NO TACCHI!"
and the wise man who said that "it pays to be conservative at times."
Maintain your cool outside–protect the warm cave excavated in your chest.
Hold steady. Stay the course; Stay the mandate. Keep your eyes on the
road. Take 10 towels and 10 hands and wipe your face. You'll be fine,
trust me. And when it does confront you, you can recite this: Modem
talking, modern walking in the streets (New desire). Take me higher,
lift me higher with your sneed (I need child). Get your sweet & tight, if
you wanna see me, stalking on the net (I know the way you like it). Get
your NFTs, cause I need no money. All I wanna groom IS. YOU. BABY.
CUNNY IN THE
90S
IS A NEW WAY I LIKE /tv/
CUTE. AND. FUNNY IN THE 90S
COME ON CHILD RUN TO ME
WE. LOVE. CUNNY IN THE 90S
IS A NUDE WAY TO SET ME FREE
IT'S. JUST. CUNNY IN THE 90S
YES I WANNA UOHHHHH
YES I WANNA SEE
Note: holeinmyheart is now canceled.
E

Personally, I have another "first Cousin problem."
Note: holeinmyheart is now double-canceled. It's not clear what he was thinking
here, but for some reason he decided to double down in order to perform the art of
multi-cancel drifting, thus ending his internet career. He is finally free.
WHEN THE SUN GOES
DOWN,
WILL YOU HEAR THE CRY,
OR JUST WALK ON BY,
AND LEAVE WITHOUT A SOUND.
Okay, offensive jokes aside, idiot Harshorne brought up the "first Cousin problem" way too late. He should have brought it up during part D, because that's more akin to the to what it actually is. Although I'm still having trouble "matching" the complex analysis version to our alggeo version. WHATEVER.
Well, anyway, if we rewrite their sequence in more familiar notation, we get
 |
And uhhh.... WE'RE DONE, LOL. Thanks to part D,
 (U) is a subgroup of
(U) is a subgroup of
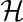 (X), so this is just the first isomorphism theorem... In fact, does the sections
even have to be global? I can replace X with open U in X and it would still
work, wouldn't it? Guess that's it.
(X), so this is just the first isomorphism theorem... In fact, does the sections
even have to be global? I can replace X with open U in X and it would still
work, wouldn't it? Guess that's it.
Next exercise is the last one of this section. Hartshorned II is almost at its first season
finale. Yayyyyy!!! Also shoutout to cyuucat
for the tip on how2glowtext. (Although I'm sure they disavow my use of it)