I.1.9

12/20/20

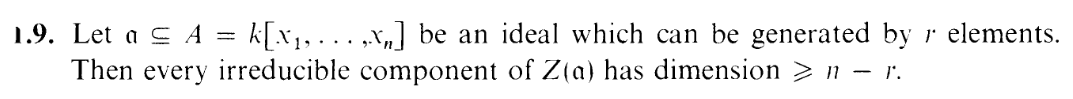
A frightening exercise if you’re clueless, but if you follow the thread of the previous exercise, then you’ll get there.

I’m going to write α = 𝔞 for this post since it looks nicer when sent through htlatex. Now, letting Y = Z(α) break up Y into irreducible components

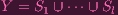Y = S1 ∪ ⋅⋅⋅∪ Sl

Like before, letting d = dimS₁, our goal is to show that d ≥ n - r

Suppose α = (f₁,…,f_r).
Like in the last exercise, we know that J is a minimal prime containing α. Now let β = (f₂,…f_r), so that α = (f₁) + β. Now, unlike the last exercise, β isn’t prime, so let’s consider a minimal prime ideal P containing β. Then, like in the last exercise,

dimA∕P	= ht(J∕P) + dim(A∕P)∕(J∕P)
	= ht(J∕P) + dimA∕J
	= ht(J∕P) + d
d	= dimA∕P - ht(J∕P)

Now, what is ht(J∕P)? Like the last exercise, since J∕P is a minimal prime containing ([f₁]) we know that if [f₁] is a nonunit nonzerodivisor, then it’s 1.

But what if it isn’t? Let’s look back at yesterday’s work as a guide:

LEMMA: π(f) is a nonzerodivisor:
Well, since P is prime, A∕P is an integral domain, so it has no nonzero zerodivisors. So if π(f) is nonzero, it’s not a zerodivisor. And [f] = [0]f ∈ P = ⇒ (f) ⊂ PZ(f) ⊃ Z(P)H ⊃ Y contradicting the Y ⊈ H assumption from the exercise. So we’re done.

LEMMA: π(f) is a nonunit:
[f][g] = [1][fg - 1] = [0]fg - 1 ∈ P
Now, err, I got worried here for a while. How does this give you a contradiction? Well, 1 is a special term in a ring, so let’s isolate it:
fg - 1 ∈ Pfg - 1 = p (where p ∈ P), so fg -p = 1 But this means that (f) + P = (1)Y ∩H = AⁿH = Aⁿ a contradiction since H is a hypersurface. DUN.

So if it’s a nonzerodivisor, I know that f₁ ∈ P, which means that [f₁] = 0 in A∕P, so J∕P is a minimal prime containing 0, i.e. J∕P = 0

ht(J∕P) = 0. This is actually good. I’ll explain later, but first let’s handle the nonunit case.

Okay, so it turns out for the nonunit case my work above turns out to be wrong LOLOLOLOLOLOLOLOLOL FUCK. WHY DO I TRY TO DO MATH WHEN I ALWAYS FAIL AT IT? Yes, I made an error in the last exercise. The part up to (f) + P = 1 is correct but if you Z both sides you get Y ∩ H = ∅, not Aⁿ. Now, that doesn’t cause any problems for the previous exercise, because the empty set case is also trivial (there are no irreducible components so the result is vacuously true). Does the same argument work here? Well, we have (f₁) + P = (1), and if you Z both sides you get Z(f₁) ∩ Z(P) = ∅, which... isn’t very helpful. Fuck. What do? Fucking heck. Now if we instead had Z(f₁) ∩ Z(β) = ∅, we’d be fine, because that joins to form Y = ∅, which is the vacuous case, but we don’t necessarily have Z(P) = Z(f₂,…,f_n)... WHAT DO? AAAAAAAAAAAAAAA.

My head is spinning. The problem with doing math is that everything just feels all over the fucking place. Not a good way to cap a day where my head has already been spinning in idleness. Jeez, my hair has been growing pretty long. I just pulled out a hefty clump of hair that got stuck in the boxfan running next to me. Apologies for the grotesque image, but that’s about the most interesting thing that will happen to someone extending their nocturnal pirouettes to 5:30am. I’m a shut-in after all. Are you? We’re approaching Xmas and we’re both lazy. A head of hair for a gold watch? Hey babe, I’ll trade my hair clump for the spinach stuck between your incisors. No? Okay, until then I’m a ballerina. Plie, releve, releve, a lanky attitude. Tip, tip, tippy tip on my tip toes, on the carpet.

When picking P, we were picking ANY minimal prime. So if there happens to be a minimal prime where [f₁] turns out to be a nonunit, just pick that one and we don’t have to deal with this case. But what if [f₁] is a nonunit for EVERY minimal prime? Well, remember, minimal primes containing β correspond to irreducible components of Z(β). And there are finitely many such components since Z(β) ⊂ Y is Noetherian. Take the decomposition Z(β) = Z(P₁) ∪ ⋅⋅⋅

∪ Z(P_s), and we have (f₁) + P_i = (1) for all i. Then

∏ _i=1^s((f₁) + P_i)	= (1)
⋃ _i=1^sZ(f₁) ∩ Z(P_i)	= ∅	Taking Z of both sides
Z(f₁) ∩⋃ _i=1^sZ(P_i)	= ∅
Z(f₁) ∩ Z(β)	= ∅
Z(f₁,f₂,…,f_r)	= ∅
Y	= ∅

Which is the vacuous case.

So, yes, we can assume that [f₁] is a nonunit. Fuck. That was a long diversion.

So basically, we have ht(J∕P) = 1or0 i.e. ht(J∕P) ≥ 1. Hence,

d ≥ dimA ∕P - 1

(1)

Now what? Well. P is the a minimal prime ideal containing β = (f₂,…,f_r), so we can just repeat the same process that we did for J and α. I.e. Let δ = (f₃,…,f_r) and let P′ be the smallest prime containing δ. Then we’ll get

dimA ∕P ≥ dim A ∕P′ - 1

(2)

So plugging it into the earlier equation,

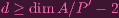d ≥ dim A ∕P′ - 2

(3)

Just keep repeating the process, until you’re left with

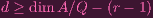d ≥ dim A ∕Q - (r- 1)

(4)

where Q is a minimal prime containing (f_r). It’s easy to show that ht(Q) ≤ 1 (Set P to be the minimal prime containing (0), i.e. P = (0) and repeat the same fucky argument as above). So

dimA	= dimA∕Q + ht(Q)
	≤ dimA∕Q + 1
dimA∕Q	≥ dimA - 1
	= n - 1

Plugging this in up there, we get

d	≥ n - 1 - (r - 1)
	= n - r

So we’re done.

We’re done... but this was a notational clusterfuck. I was redefining stuff over and over again. But it reflects my thought process more than a nice and pretty proof, so I guess it’s appropriate. If reading this proof confused you, well, that’s how math ”feels” in my head much of the time.

And what about the visual picture associated with this? This proof heavily relies on quotienting, and I haven’t quite formed a picture of what quotients represent in algebraic geometry, so I’m not sure of the picture. I understand the picture behind the result–that’s easy to construct, but not the picture behind the proof. Ehh.... I’ll think about it later. Twirl.

ERRATA on 1.8:

Covered above hehe.

MISC:

Jesus, the "s" on top of the product and union notations look awful. On the other hand, the numbered equations look nice (...even though I didn't even use the numbers for anything).

← I.1.8 I.1.7a →