I.5.8
8/19/2021

p3nor in the B—˙—TT. ← The formation in place of the "U" is meant to
represent duality: One man will see it as that moment in Breakout when
your ball goes past a gap in the bricks–that orgasmic moment where you
know your ball is about to bounce off the ceiling and wipe out a generous
amount off the upper layers on your behalf, and all you have to do is
kick your feet up on the paddle and watch the glorious destruction. The
other man will realize that the ball is positioned equidistant between the
bricks–thus it actually just went straight up through the gap... and it's going to
just bounce off the ceiling and come right back down through the gap.
Yes, duality. The glass half full, vs. the glass half empty. Yang vs. Yin. The
proposer vs. the contrarian. The Good vs. the Bad. Heads vs. tails. *Flips coin,
and catches it between my hands* ...And then there's me. Who am I, you ask?
Well, think of me as The Third Man. The Other. The Missing Link. The
Forgotten One. The Dark Friend.
Listen, young one: You ever hear that old tale? There was once a man
walking through a dark alley, and suddenly he sees a pair of headlights
approaching him at a high speed. And our young man is terrified, terrified,
terrified. He's going to die, at this rate. Oh don't cry loved one *kisses your
forehead* please don't cry, my baby *smooch, smooch, smooch* it's just a
story *smooch, smooch, smooch*. Keep listening, young one. For those
headlights were approaching, and approaching, and approaching, and the man
stood there, poised to accept his fate, philosophically realized as Dasein,
being towards death (what?). Yes, it was coming. It was coming, coming,
coming, coming, oh don't be scared *smooch, smooch* for it was coming,
coming, coming, coming, AND IT CAME.... IT CAME... and it passed...
And the man was... okay. He was fine! He was alive! For those headlights
were not the headlights of a car, but those of two motorcycles. Indeed,
there was a gap where one did not expect. The Unexpected Gap. And
this brings me to myself: My True Identity. For I am the One who sees
the two dashes as not separate bricks, but a single entity: The paddle
itself. Indeed, this is a special game of breakout where there is a gap in
the middle of the paddle. The ball isn't moving up. It's moving down.
It is, in fact, about to go through the very gap. And you, the player,
had better move that paddle to save it from ruin. I am... *reveals coin*

..........................
Shocked? Traumatized? I know. I'm sorry for hiding it from you, but I had no
other choice. I had to. Not just for my safety... but for yours. *Grabs your cheeks
and brings your face close to mine* I'm sorry.... I just didn't want you to be in
danger.... I love you... I love you. *Passionately kisses you on the lips*........ I have
to go now. "Wait, not yet!" ........ I have to. It's my duty. "Well.... you better come
back, or I'll be really mad!" Heh... Who do you think I am? *Jumps into the
darkness*
Okay, the joke is that I tried to type a bar, underscore, and another bar to
1337 a U, but Latex did that weird dash dot dash formation instead.
"BOOOOOOOO, YOU'RE SO SLOW AT MAKING POSTS" Yes, yes, I know. I
have not yet reaccustomed myself to my trademark daily posting rate, which...
has never actually occurred on this blog...
By the way, some of these exercises were done long back enough that I'm
forgetting whether I actually finished them. I almost skipped writing this post
because my notes made it look like I gave up. BUT I DIDN'T. Check it out.

Let's follow Harty's Hint: The Trilogy. First, we need to show that the choice of
homog coords doesn't matter for the rank. Let's denote
| di | = deg fi |
EVERYONE STOP. I DROPPED MY PROOF.
I just realized that, in my notes, I mistakenly assumed that the partial derivatives
would be homogenous. But that's obviously not the case (e.g. differentiate
x02 + x1x2 with respect to any variable). Sooooo my argument for (a) breaks
down.
Errrr.... Okay... let's just assume (a) for now. RANK IS INDEPENDENT OF
CHOICE OF HOMOGENOUS COORDINATES. Fine. Let's just get to the main
part. We'll start with the "only if" condition.
Assume P is nonsingular on Y , and assume without loss of generality that it's in
the open affine U0 = {x0≠0}, so we can write P = (1,a1,…,an) (and thanks
to (a), the rank of the matrix will hold for this choice of coordinates).
Let's denote
| gi(x1,…,xn) | = fi(1,x1,…,xn) |
The gi determine Y ∩U0 (I'll call this set Y 0). So we have two Jacobians in
play. One for Y :
| J | =
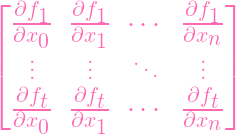 | (1) |
And the other for Y 0:
| J0 | =
 | (2) |
And these matrices are obviously related. For the "only if" (
 ) we need to
show that rkJ = n - r.
) we need to
show that rkJ = n - r.
Well, since dim X = dim X, we have that dim Y 0 = dim Y = r. And since
Y 0 is affine, it's well known to us that its Jacobian J0 has rank n-r. So really,
our problem reduces to rkJ0 = n - r
 rkJ = n - r. But how is J related
to J0?
rkJ = n - r. But how is J related
to J0?
Recall we set P = (1,a1,…,an) ∈ Y . Let's get the corresponding point for
Y 0 : Q = (a1,…,an) (we know it's in Y 0 because it satisfies the gi).
Now, reader, CONVINCE YOURSELF OF THIS:
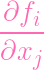 (P) (P) | =
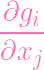 (Q) (Q) | (when j≠0) |
Indeed, when you differentiate with respect to a variable that isn't x0, those
terms stay constant. So it doesn't matter if you plug in 1 after differentiating to
obtain the left hand side, or before differentiating to obtain the right hand side.
Hence we have
| J(P) | =
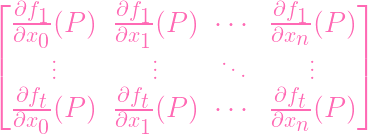 | (3) |
=
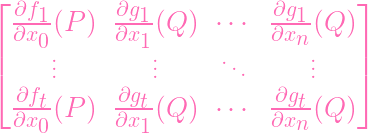 | (4) | |
=
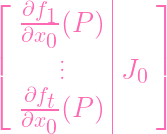 | (5) |
So J0 is a submatrix of J. Hence
| rkJ ≥ rkJ0 |
Yaaaaaaaaay...... Wait that's only ≥.... I need to show =.... Errrr.... LET'S
GO BACK TO (1). And actually, I'm gonna transpose it this time (which is
fine).
| JT | =
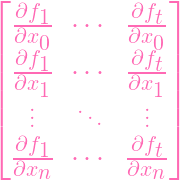 |
Now, that top row is the pesky row that doesn't just "turn into J0" after we
plug in P. However, I can use the hint and do something special with it. Using
zero-based indexing, if I multiply the ith row by i and add every row to the first
row, then Euler's lemma tells me I get
 |
And since fi(P) = 0 for all P, plugging in P turns this matrix into
![[ ]
0 ⋅⋅ ⋅ 0
J0](Ip5p812x.png) | (6) |
Since J0 has rank n - r and can be put into an RREF with n - r
pivots accordingly, and since the top row is a zero row, the RREF of this
matrix has exactly n - r pivots. So the rank is EQUAL (=) to n - r
⇐=
So this time we're assuming that rkJ = n - r. Again assuming out point is in
U0, we can reduce to the affine Y 0 given by the gis, and showing that P is
nonsingular in Y 0 is equivalent to proving that rkJ0 = n - r. So now our goal
is showing rkJ = n - r
 rkJ0 = n - r. Using the same logic, we can
row-reduce J to (6). This time we know that the whole matrix has rank n - r.
But since the top row is just 0, we know the RREF of the rest of the matrix has
n-r pivots. I.e. rkJ0 = n-r. PWNED (actually no, that wasn't slick at all; I
shouldn't have had to even split this ⇔ into its component implications).
rkJ0 = n - r. Using the same logic, we can
row-reduce J to (6). This time we know that the whole matrix has rank n - r.
But since the top row is just 0, we know the RREF of the rest of the matrix has
n-r pivots. I.e. rkJ0 = n-r. PWNED (actually no, that wasn't slick at all; I
shouldn't have had to even split this ⇔ into its component implications).
Hmmm? Oh, I put off showing that rank is independent of homogenous
coordinates. Heh. Well, now the time has come...... TO RUN AWAY.

逃げるが勝ち
